AtCoder题解——Beginner Contest 168——E - ∙ (Bullet)
题目相关
题目链接
AtCoder Beginner Contest 168 E题,https://atcoder.jp/contests/abc168/tasks/abc168_e。
Problem Statement
We have caught N sardines. The deliciousness and fragrantness of the ii-th sardine is Ai and Bi, respectively.
We will choose one or more of these sardines and put them into a cooler. However, two sardines on bad terms cannot be chosen at the same time.
The ii-th and j-th sardines (i≠j) are on bad terms if and only if Ai⋅Aj+Bi⋅Bj=0.
In how many ways can we choose the set of sardines to put into the cooler? Since the count can be enormous, print it modulo 1000000007.
Input
Input is given from Standard Input in the following format:
N
A1 B1
:
AN BNOutput
Print the count modulo 1000000007.
Samples1
Sample Input 1
3
1 2
-1 1
2 -1Sample Output 1
5
Explaination
There are five ways to choose the set of sardines, as follows:
- The 1-st
- The 1-st and 2-nd
- The 2-nd
- The 2-nd and 3-rd
- The 3-rd
Samples2
Sample Input 2
10
3 2
3 2
-1 1
2 -1
-3 -9
-8 12
7 7
8 1
8 2
8 4Sample Output 2
479Constraints
- All values in input are integers.
- 1 ≤ N ≤ 2×10^5
- −10^18 ≤ Ai, Bi ≤10^18
题解报告
非常惭愧,本题在现场比赛的时候,我竟然没有 AC。
题目翻译
我们抓住 N 条沙丁鱼,第 i 条鱼的美味度和芳香度分别用 Ai 和 Bi 表示。现在我们将选择一条或者两条条沙丁鱼放置到冷柜中,如果 ![]() ,那么这第 i 条和第 j 条沙丁鱼就不能放在一起。
,那么这第 i 条和第 j 条沙丁鱼就不能放在一起。
问我们有多少种放置的方法。由于数据会比较大,请将答案对 1000000007 取模。
题目分析
可能不少人看到题目的时候,都不知道题目深层次到底说什么。我开始的时候,这个题目也没有完全读懂。第一反应是暴力枚举,但是看到了数据集 N 的大小,暴力枚举肯定是无法通过。
数学知识
向量的点乘
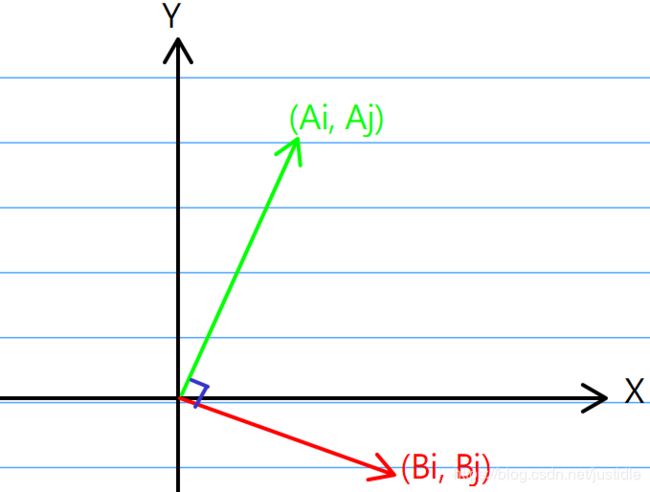
我们仔细的看一下题目中提到的公式:![]() ,是不是看上去很眼熟?不错,这不就是向量中的点乘的定义吗?所以还是强调一下,算法核心还是数学。这个公式的表示向量 A 和 B 是垂直的,如下图。
,是不是看上去很眼熟?不错,这不就是向量中的点乘的定义吗?所以还是强调一下,算法核心还是数学。这个公式的表示向量 A 和 B 是垂直的,如下图。
模的化简
向量有两个要素:模和幅角。如上图所示的向量,我们可以将他们的 (Ai, Aj) 进行化简,化简的目的是为了降低数据的复杂度,也就是降低了有效的 N 的范围。
化简的方法也简单,就是除以 Ai 和 Aj 的最大公约数即可。
幅角的化简
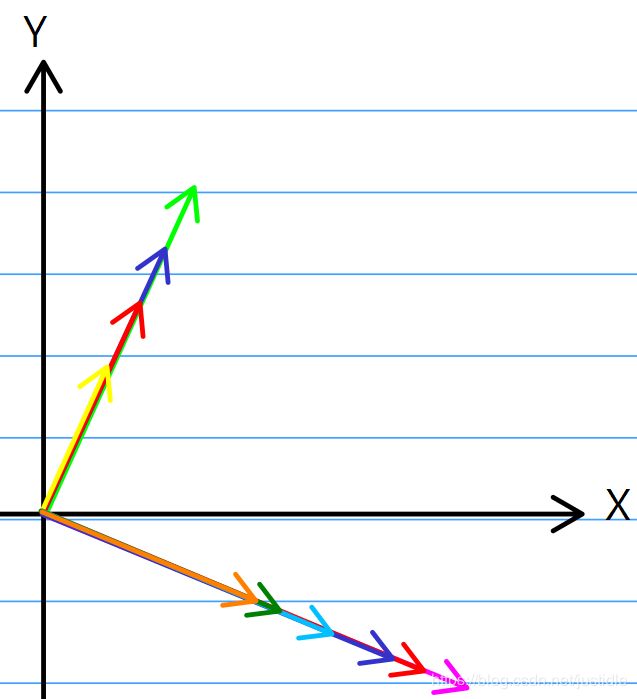
本题中,幅角没有什么意义,因此我们可以将第三象限的向量转换为第一象限,将第二象限的向量转换为第四象限。这个处理的目的和模化简得目的是一样的。
最终答案
如上图所示,我们有若干个向量互相垂直,注意不垂直的向量没有绘制。
我们选择任意一个向量,假设其坐标为 (x, y)。
1、有 K1 个向量,与该向量不垂直。这种情况下每个属于该类的沙丁鱼,我们可以选或者不选。显然存在 ![]() 种方案,
种方案,
2、有 K2 个向量,与该向量垂直。这种情况下每个属于该类的沙丁鱼,我们只能选择两种中的一个。因此方案为 ![]() 。
。
由于两种方案都不选在上面多算了一次,所以总方案数位:![]() 。
。
样例数据分析
样例数据 1
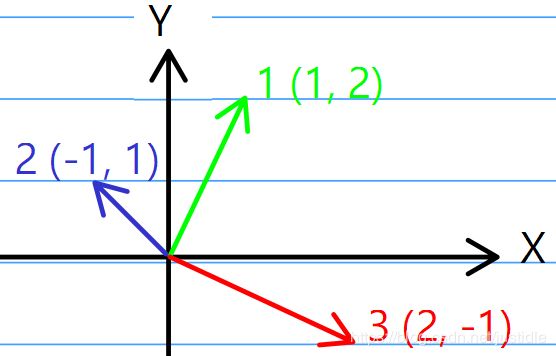
根据样例数据 1,我们可以绘制出分布如下图。
根据题目的要求,放置沙丁鱼的原则有两种:
1、一条放置。这样我们有 3 种选择:即单独放第 1 条;单独放第 2 条;单独放第 3 条.
2、两条放置。如上图所示,我们知道绿色和红色是垂直关系。这样我们有 2 种选择:放置 1 和 2;放置 1 和 3;放置 2 和 3。
合计是 2+3=5 种。
根据上面的计算公式:对于 (1, 2) 这个向量,和它不垂直有 2 个,和它垂直有 1 个,因此根据计算公式:K1=2,K2=1,![]() 。
。
样例数据 2
有点多,我偷懒了,略。
数据表示
我们可以将每一个 Ai, Aj 用 map 来表示。定义方法如下:
map, long long> m; 也就是统计 (Ai, Aj) 这样的最简向量个数。
算法设计
1、逐个读取 Ai 和 Aj。
2、如果 Ai 和 Aj 同时为零。记录这样向量个数,后续的处理就不需要了。
3、如果 Ai 和 Aj 不同时为零。进行约分处理和象限处理。生成 map 对。
4、遍历 map,进行有效性检查。
OI 知识点
1、快速幂。
2、最小公约数。
3、余数相关定理。即如何取模。
AC 参考代码
#include
using namespace std;
const long long MOD=1e9+7;
long long quick_power(long long x, long long y, long long p) {
long long ans=1;
while (y) {
if (y&1) {
ans=(ans*x)%p;
}
y>>=1;
x=(x*x)%p;
}
return ans%p;
}
int main() {
long long n;
long long zeros = 0;
long long ans=1;
map,long long> m;
map,long long>::iterator it;
scanf("%lld", &n);
for (long long i=1; i<=n; i++) {
long long u,v,now;
scanf("%lld%lld", &u, &v);
if (u==0&&v==0) {
zeros++;
continue;
}
now=__gcd(u,v);
u/=now;
v/=now;
if (u<0) {
u=-u;
v=-v;
}
m[make_pair(u,v)]++;
}
for (it=m.begin();it!=m.end();it++) {
if (it->second==0) {
continue;
}
long long x=it->first.first,y=it->first.second;
long long p=quick_power(2, m[make_pair(x,y)], MOD);
y=-y;
if (y<0) {
x=-x;
y=-y;
}
if (m.count(make_pair(y,x))) {
p=(p+quick_power(2, m[make_pair(y,x)], MOD)-1);
m[make_pair(y,x)]=0;
}
ans=(ans*p)%MOD;
}
printf("%lld\n", ((ans+zeros-1)%MOD+MOD)%MOD);
return 0;
}