【文献阅读】Probabilistic Terrain Mapping for Mobile Robots With Uncertain Localization

“Probabilistic Terrain Mapping for Mobile Robots With Uncertain Localization”是ETH的四足机器人组的一个研究子项目，其动机是研究如何用机器人摄像机逐帧相对运动和3D点云观测对机器人的局部地面地形进行重构建模，用来做局部规划和四足里面的足迹落点控制。该文发在2018 RA-L上，有ROS代码。

1. 整体框架

该文在他们先前工作“ROBOT-CENTRIC ELEVATION MAPPING WITH UNCERTAINTY ESTIMATES”上改进得到，局部地形评估有一个经典工作是2007年的“Real-time localization and elevation mapping within urban search and rescue scenarios”，发表在著名应用期刊Journal of Field Robotics上，写的很好。
该文主要框架是
一共三个模块，一是把观测信息融合到栅格地图，二是把机器人移动融合到栅格地图，即是把位姿估计不确定性体现到栅格地图里。最后是地图融合模块，这个模块的存在是因为第一二步处理的栅格地图是自定义的概率栅格地图，每个点（x,y）包含各自期望和方差，这一步把期望，置信上下界确定出来，导出我们常见的二维栅格地图（类似costmap）。

2. 符号与坐标系定义

如上定义4个坐标系$\mathbf{I},\mathbf{B},\mathbf{S},\mathbf{M}$，惯性系$\mathbf{I}$固定在真实世界地形上，机器人base系$\mathbf{B}$和传感器系$\mathbf{S}$固定连接。$\mathbf{I}$和$\mathbf{B}$之间关系有姿态估计确定：平移$r_{IB}$和旋转${\Phi }_{IB}$，并由6维协方差阵表示不确定性：

为了后面好处理，这里的旋转拆分为两部分：

前者包含yaw变换，后面包含pitch和roll。
最后看地图坐标系$\mathbf{M}$。${\Phi }_{BM}$规定为：yaw方向随着$\mathbf{B}$转，pitch，roll方向和$\mathbf{I}$保持一致。而$r_{BM}$原文没有明确说明，不过按上下文推应该是某个固定值，这并无关系。

3. 由观测更新地图

传感器是realsense这类RGB-D相机的点云，观测结果用${}_s{r}_{sp}$表示（传感器到P点距离sp在s坐标系下的表示）。地图M是2.5d栅格地图，即每个元素是用$(x_i,y_i,\widetilde{p_i})表达的。其中$$\tilde{p}\sim \mathcal{N}(p,{\sigma }_p^2)$是${}_s{r}_{sp}$映射到地图坐标系后的高。那么有：

其中P是映射阵：P=[0,0,1]。
而方差${\sigma }_p^2$稍微难求一点，涉及到方差传播（可见上一博客）：

其中：

这个偏导数并非普通矩阵求导，我们处理的是参数化的旋转矩阵，其微分应用李代数解决。通过阅读文献《A Primer on the Differential Calculus of 3D Orientations》得知其推导方法
该文献推了一遍与旋转阵相关的所有式子，首先介绍其符号体系：


注意，从后文可知这里映射C是广义的，也表示欧拉角或单位四元数参数化的旋转到其${\mathbb{R}}^{3\times 3}$矩阵表示的映射！！公式1 2 3是向量对应的反对称阵的三条小性质。略去中间大量内容直接看偏导数推导：

上面推导是拿出向量导数每一元素推的，每个元素都一样，这样写省纸。第五个等号是叉乘的反交换率
上面推导用到的性质20,14,5,12在此摘录下来：

为简化书写定义的两个二元运算符（box add与box sub）


注：式5看做算子方程即可理解，并不是旋转矩阵
最后是著名的罗氏公式：

至此解决了对上面雅克比矩阵的疑问，回到原文献，还有两个问题需要说明，一是${\Sigma }_S$是相机误差模型，实际就是通过实验把深度相机测的点云在x,y,z三方向的误差测出来。二是${\Sigma }_{{\Phi }_{IS}}$，这仅包含旋转估计的不确定性，而平移估计不确定性在后面的由运动更新的部分考虑。
推出$(p,{\sigma }_p^2)$后，用经典的卡尔曼滤波做一下地图和观测的融合：

此处有个小细节，当相机看到一堵墙，导致一堆点摞在一起映射到同一(x,y)咋办？解决方法大概是，取最高的那个，剩下的扔了，这是仿照了《Real-time localization and elevation mapping within urban search and rescue scenarios》的做法。

4. 由运动更新地图

现在处理由于运动估计不准确导致的地图不确定性。由于两帧之间姿态估计肯定会有偏差，故测到的地图会越来越飘，这可以通过栅格地图元素x,y方向的方差体现。作者扩展经典栅格地图，对每一元素记录x,y和高度三个方差，当观测到点p得到其测量结果时，将协方差阵赋值为如下初值：

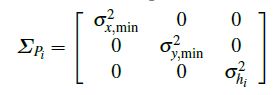
这是因为之前设定地图坐标系和base坐标系是随动的，观测精度是很高的，因此每次观测就可消除对应点的位置不确定性。${\sigma }_{x,min}^2，{\sigma }_{y,min}^2$ 是两个小量，作者设为$(d/2{)}^2$其中d为栅格边长。
下面推导两帧之间位姿变换的误差传播：


（8）式给出点P位置在$M_1,M_2$俩参考系之间的传播。亦可等价写作：

这时作者提出可如下指定参考系$M_2$：

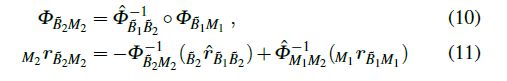
使得凑出如下性质：

也就是说$M_1,M_2$便重合了，于是可统一到一个固定的$M$系下。那么和之前一样，设不确定模型为高斯，研究协方差传播方程：

其中${\Sigma }_P,{\Sigma }_{\Phi }$是由${\Sigma }_{IB}$导出的，并不简单，详见原文附录。
类似之前雅克比阵求法，可推出：

5. 地图融合

也就是如下过程：

这块相对简单，对cell i，考虑其附近的cell j（附近指在对方$2\sigma$椭圆内），类似混合高斯，加权求和便可得cell i 的概率分布函数，然后置信上下界便好求了。
这一步骤只在需要查询地图的时候执行，也就是说平时观测和融合都只需在$(\widehat{h_i},{\Sigma }_{P_i})$这个图上维护即可，省了很多计算量，这个地图融合步骤有点观测器的意味。

6. 拓展到动态环境

为处理环境动态变化，比如地上凳子忽然被撤走，作者搞了两个trick。
第一是发现传感器测距值忽然变小（对应真实地面变高）超过一定阈值（采用马氏距离为依据），那么就人为给地图加噪，降低对地图的信任，让卡尔曼滤波器尽快信任传感器加速响应：

第二是遇到上面相反的情景时候（对应真实地面变低）：

提出一种可视化检查的方法。具体做法是是发现传感器测距值忽然变大（对应真实地面变低）超过一定程度时，就丢弃地图上对应老点，很巧妙。这俩trick同时使用，互补的，基本就可解决动态环境适应问题。
最后作者的实验主要是在自己的四足上弄的，图画的很漂亮，很值得学习：


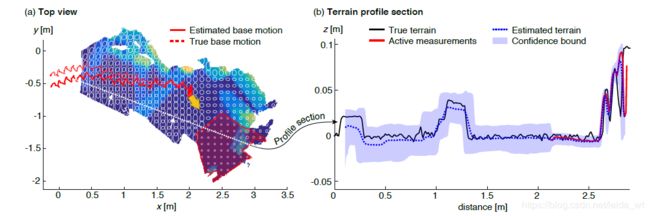
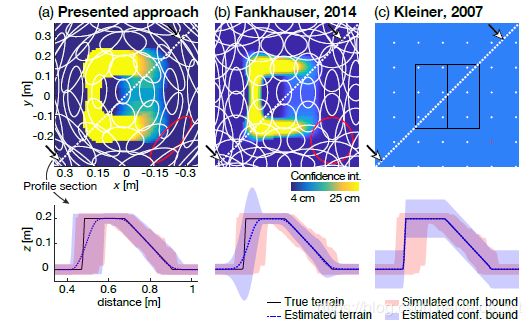
源代码可见https://github.com/ANYbotics/elevation_mapping用了他们自己的写的一个ROS包https://github.com/anybotics/grid_map，这个包拓展了ROS里的costmap到一个多层的，方便把方差什么的放进去，并提供到costmap消息的转换。

总结

贴一下conclusion原文翻译：

我们已经提出了一种新的海拔映射方法，该方法解决了在带有本体感受状态估计的移动机器人上经常发生的定位漂移问题。 提出的方法估计了以机器人为中心的坐标系中的高程图，使得将新测量结果集成到该图中的过程仅受范围传感器噪声以及可观察到的侧倾角和俯仰角的不确定性影响。 地图中的数据基于机器人移动时增量运动的不确定性进行更新 。这可以使机器人在任何时间点从其局部角度估计地形。 通过将方法拆分为数据收集（从距离测量和机器人运动中进行地图更新）和地图融合步骤，我们降低了映射过程的计算负担。这使得能够可靠地进行实时高程映射，而与视听定位方法无关。 我们将说明制图过程如何估计具有相应置信区间的地形剖面，并显示估计的分布如何与模拟和真实实验中的地面真实情况参考相匹配。当与腿式机器人一起使用时，这项工作的当前局限性是突出的。 在机器人采取许多步骤的情况下，由于定位的漂移，机器人下方的地形图不确定性增加，这给机器人的地形感知控制带来了困难。 在我们当前的工作中，我们通过面朝下的深度传感器，更准确的定位以及将立足点与地形图进行匹配以提供定位反馈来应对这一挑战。

总的来看，在slam和机器人相关领域，搞清楚旋转矩阵很有必要，可参考：
Differential Geometry and Lie Groups A Computational Perspective
Differential Geometry and Lie Groups A Second Course
State Estimation for Robotics