软考——算法及常用排序算法总结

概念

    算法可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤。或者看成按照要求设计好的有限的确切的计算序列，并且这样的步骤和序列可以解决一类问题。

特征

       一个算法应该具有以下五个重要的特征：

       1、有穷性（Finiteness）

             算法的有穷性是指算法必须能在执行有限个步骤之后终止；

       2、确定性(Definiteness)

             算法的每一步骤必须有确切的定义；

       3、输入项(Input)

             一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输入是指算法本身定出了初始条件；

       4、输出项(Output)

             一个算法有一个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的；

       5、可行性(Effectiveness)

            算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步，即每个计算步都可以在有限时间内完成      （也称之为有效性）。

算法性能比较

       1.时间复杂度

          算法的时间复杂度是指执行算法所需要的计算工作量。一般来说，计算机算法是问题规模n的函数f(n)，算法的           时间复杂度也因此记做：  T(n)=Ο(f(n))

        因此，问题的规模n越大，算法执行的时间的增长率与f(n) 的增长率正相关，称作渐进时间复杂度。

      2.空间复杂度

          算法的空间复杂度是指算法需要消耗的内存空间。其计算和表示方法与时间复杂度类似，一般都用复杂度的渐近性来表示。同时间复杂度相比，空间复杂度的分析要简单得多。

排序算法

      直接插入排序

        每次从无序表中取出第一个元素，把它插入到有序表的合适位置，使有序表仍然有序。对于具有n个记录的          文件，要进行n-1趟排序。

   例：

       对15 45 46 58 18 10 62有小到大排序

    第一次排序

    取第二个数45，与第一个数比较15<45，所以45插到15之后

    15 45 46 58 18 10 62

    第二次排序

    取第三个数46 ，分别与已排好的第一、第二个数比较，15<46,45<46,所以58插到46之后。

    序列：15 45 46 58 18 10 62

    第三次排序

    取第四个数58，分别于排好的第一、第二、第三个数比较，15<58,45<58,46<58,所以58插到46之后。

    序列：15 45 46 58 18 10 62

    第四次排序

    取第五个数18，分别与排好的第一、第二、第三、第四个数比较，15<18,45>18,46>18,58>18,所以18插到15之后。

    序列：15 18 45 46 58 10 62。

    以此类推第五、六…..次排序。

    结果序列

         10 15 18  45 46 58 62

  算法性能

    时间复杂度：O(n^2)

    空间复杂度：O(1)

 

希尔排序

    希尔排序又称缩小增量排序，是插入排序的一种。希尔排序属于插入类排序,是将整个无序列分割成若干小的子序列分别进行插入排序。排序过程：先取一个正整数d1元素放一组，组内进行直接插入排序；然后取d2一般d1=n/2,di+1=di/2,如果di为偶数，则加1，保证di为奇数。

     例：

       对15 45 46 58 18 10 62有小到大排序

 算法性能

   时间复杂度：O(n^1.3)

   空间复杂度：O(1)

堆排序

   堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，可以利用数组的特点快速定位指定索引的元素。堆实质上是满足如下性质的完全二叉树：树中任一非叶子结点的关键字均不大于（或不小于）其左右孩子（若存在）结点的关键字。利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

   其基本思想为(大顶堆)：

    1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；

    2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n]; 

    3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

   操作过程如下：

    1)初始化堆：将R[1..n]构造为堆；

    2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

   因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

   例

    对15 45 46 58 18 10 62有小到大排序

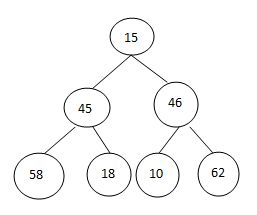
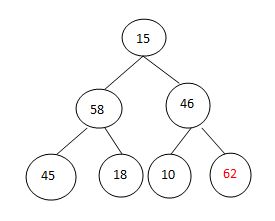
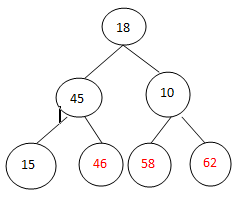
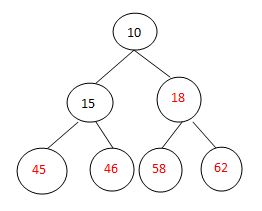
    初始建立完全二叉树：

     构造初始堆：

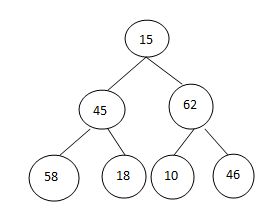
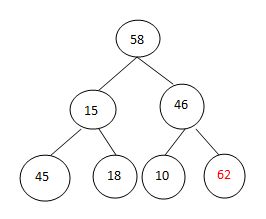
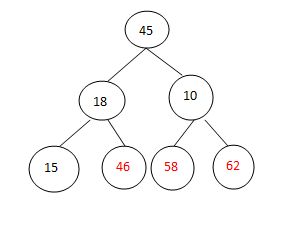
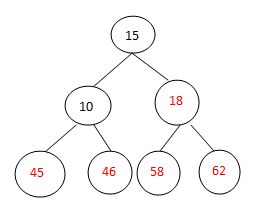
      交换排序：

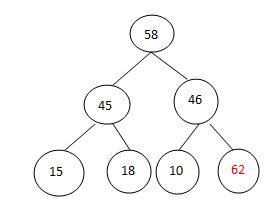
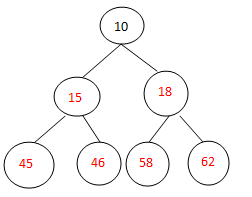
      调整：

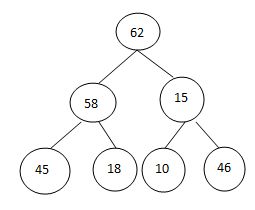
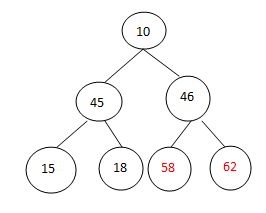
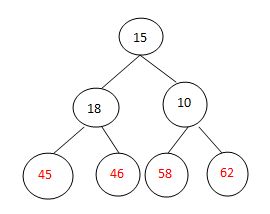
     交换排序：

     调整：

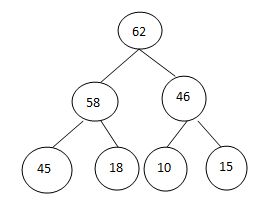
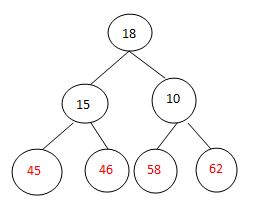
     交换排序：

    调整：

     交换排序

     调整：

     交换排序：

     调整

     交换排序：

   

   算法性能

    时间复杂度 O(nlogn)

    空间复杂度 0(1)

基数排序

    基数排序的基本思想：从低位到高位依次对Kj(j=d-1，d-2，…，0)进行箱排序。

    例：

    对15 45 46 58 18 10 62有小到大排序

   第一次排序(个位排序)

       0    1    2   3   4    5    6   7   8   9

       10       62             15   46     58

                                    45            18

   排序序列：10 62  15  45 46 58 18

   十位排序

          0     1     2     3     4    5    6    7    8    9

                 10                 45   58  62

                 15                 46

                 18

   排序结果序列：10 15 18 45 46 58 62

      算法性能

    基数排序的时间是线性的(即O(n))。

    基数排序所需的辅助存储空间为O(n+rd)。

    基数排序是稳定的。