Leetcode 968. Binary Tree Cameras
原题
Given a binary tree, we install cameras on the nodes of the tree.
Each camera at a node can monitor its parent, itself, and its immediate children.
Calculate the minimum number of cameras needed to monitor all nodes of the tree.
Example 1:
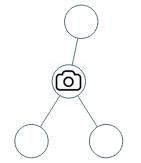
Input: [0,0,null,0,0]
Output: 1
Explanation: One camera is enough to monitor all nodes if placed as shown.
Example 2:
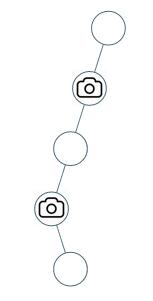
Input: [0,0,null,0,null,0,null,null,0]
Output: 2
Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
题目大意:
在二叉树节点放置摄像头,每个摄像头覆盖到父节点、本身、以及子节点,最后求得覆盖所有节点所需最小摄像头数量。
分析
Ref:https://leetcode.com/articles/binary-tree-cameras/
思路比较明确,使用动态规划来求解全局最优解。这里最主要是到对每个节点的状态划分。
由于是树形结构,按照自下到上的思路来对当前节点(cur_node)的状态进行划分,节点总共有三种状态:
状态0:
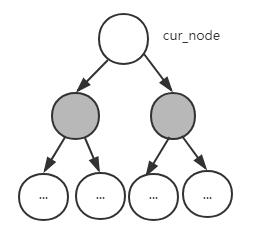
两个子节点均被覆盖,当前节点不被覆盖。
状态1:
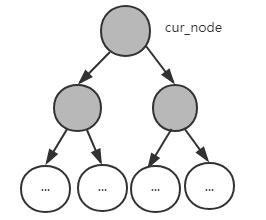
当前节点被覆盖,但是当前节点没有放置相机(说明两个子节点中至少有一个放置了相机)
状态2:
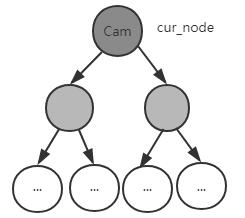
当前节点放置了相机
总结
对当前的节点进行划分之后,可以得到以下的状态转移条件
- 为了满足状态0,则cur_node的两个子节点都必须处于状态1
- 为了满足状态1,则cur_node的两个子节点中至少有一个子节点处于状态2,另一个子节点处于状态1或状态2
- 对于状态2,由于cur_node放置相机,两个子节点可以处于任何状态
递归函数定义
令solve(node)函数为求解函数,返回当node状态分别为0,1,2时,满足其子树全部被相机覆盖的最优解(dp[0], dp[1], dp[2])
即:
- 当node为状态0时,返回覆盖其子树所有节点所需的最小相机数(dp[0])
- 当node为状态1时,返回覆盖其子树所有节点所需的最小相机数(dp[1])
- 当node为状态2时,返回覆盖其子树所有节点所需的最小相机数(dp[2])
Note: 由于状态0没有覆盖到当前节点,因此要求解覆盖包含当前节点的最优解时,其解为min(dp[1], dp[2])。
递归出口
当当前节点为NULL时,跳出递归,返回解为(0, 0, MAX_VALUE),这里假设子节点为空时,可以视为被相机覆盖,MAX_VALUE表示当前节点不可能是2状态。

如上图为例,如下对只有1个或2个节点的情况进行解释:
当当前节点为NULL时,我们关注父节点(2)的状态,(这里假设子节点为空时,可以视为被相机覆盖)
- 因此节点2处于状态0时,得到的最优解为0,因为子节点均被覆盖,不需要额外相机
- 因此节点2处于状态1时,其不可能是由子节点的相机覆盖得到的,因为子节点没有放置相机,其值为MAX_VALUE
- 因此节点2处于状态2时,放置一个相机,最优解为1
只有一个节点2时,得到的节点2不同状态的最优解为(0, MAX_VALUE, 1),最优解为min(MAX_VALUE, 1) = 1.
再往回推当节点2有一个父节点1时,将节点1最为当前节点。
- 由于节点2不可能由其子节点覆盖得到,因此此状态下的最优解为MAX_VALUE,表示不可能
- 当节点1为状态1时,由子节点覆盖得到,此状态下最优解1
- 当节点1为状态2时,在此位置上放置相机,子节点可以为任何状态,此状态下最优解1
只有两个节点时,得到的节点1(root)不同状态的最优解为( MAX_VALUE, 1, 1),最优解为min(1, 1) = 1
他山之石,可以攻玉(别人的答案)
在提交之后可以看到别人提交的答案,看完后再看看自己的代码便更觉得羞涩难挡,因此去掉了贴自己代码这一步,转而分析别人代码。
作者@awice
第一次看到代码的时候反复看了几次才看懂,为了便于大家理解,以注释的形式做个笔记
class Solution {
public:
int minCameraCover(TreeNode* root)
{
vector<int> ans = solve(root);
//由于状态0不满足覆盖条件,因此当当前节点为root时, 选择满足状态1和状态2中的最小值
return min(ans[1], ans[2]);
}
vector<int> solve(TreeNode* node) {
//按照之前递归出口的分析,这里将MAX_VALUE设为了99999
if(node == NULL)
return vector<int>{0, 0, 99999};
//对当前节点的左子节点以及右子节点计算最优解值
vector<int> L = solve(node->left);
vector<int> R = solve(node->right);
//求解左子节点以及右子节点中满足的状态1、状态2的最小值
//也就是全部覆盖左子树、右子树所需相机数的最优解
int mL12 = min(L[1], L[2]);
int mR12 = min(R[1], R[2]);
//当当前节点为状态0时,按照【总结1】,两个子节点必须处于状态1.
//因此得到的最优解为L[1]+R[1]
int d0 = L[1] + R[1];
//当当前节点为状态1时,按照【总结2】,两个子节点中至少有一个节点处于状态2,另一个子节点处于状态1或2
//因此得到的最优解为这两种情况的最小值
int d1 = min(L[2] + mR12, R[2] + mL12);
//当当前节点为状态2时,按照【总结3】, 只要求得两个子节点的最优解在加上当前节点放置的相机数1即可
int d2 = 1 + min(L[0], mL12) + min(R[0], mR12);
return vector<int>{d0, d1, d2};
}
};