LCA,即最近公共祖先,就是即在一棵树中,找出两节点最近的公共祖先。
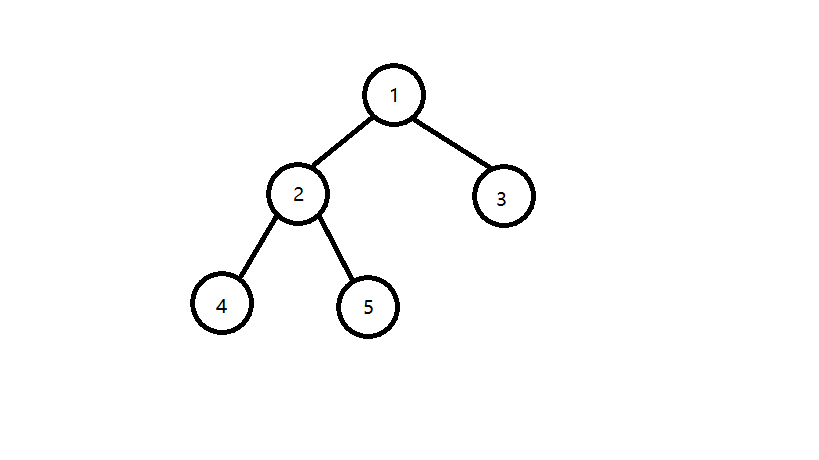
比如说这张图里的点4和点5,显而易见,他们的LCA就是2,;同理,点4和点3的LCA为1。可知,LCA就是两个点的祖先节点集中交集中离根节点最远的那个点。
特别说明一下,一个节点的祖先可以是自己。也就是说,点1和点4的LCA是点1,这个是没有毛病的·。
那么,我们就需要知道怎么求任意两点的LCA,以下介绍三种方法:
1. 暴力大法
俗话说的好,“只有大力才能出奇迹”,因此,我们必须大力发扬大力精神! /手动滑稽
2.tarjan离线
话说tarjan还真是出名,前几天学强连通分量学到了一个tarjan;学割点和桥又遇到了一个tarjan,这里又蹦出来一个tarjan。
不过这个tarjan和之前的tarjan有很大区别,连DFN和LOW都没了,主要用到dfs和并查集。
首先,有几个重要的变量:
-
vis[]:用来记录该点是否访问过;
-
father[]:相信学过并查集的人都认识吧,这里的father记录该点“当前”的祖先,这个在后面我会讲解;
用一个例子讲解

假如,我们找LCD(4,6)不难发现,点4,点6都在点4的字数上,即两点之间是连着的,不分叉,那么其最近公共祖先一定是点4.所以说假设点x和点y,假如点x(点y)在以点y(点x)为根节点的子树上,那么该根节点就是其最近公共祖先.
假如情况再复杂一点,比如说点6和点7,他俩彼此互不在彼此的子树上,怎么办?
这时候观察一下dfs序,假如从左往右dfs,那么顺序大概如下:
1-2-3-4-6-7-8-13-10-14-17-5-11-15-8-12-16-18
(其实看到7就可以了,一不小心全给打出来了)
发现,有一个转折点3,从3开始向左遍历4,6,回溯之后才遍历到了7.而且,不仅是7,上面的我给出的dfs序从7以后的每一个与点6求LCD答案都将是3.这看起来好像就有规律了.
结论:假如两个点互相不在彼此的子树上,那它俩总是在另外一个节点的子树上,而该节点就是dfs遍历中,分别向这两个支路遍历的那个节点,这个点即为最近公共祖先.
那么,我么就尝试模拟这个过程
从一个点开始dfs遍历,每遍历到一个点,就将其标记为已访问,并且将其father设为其本身,意义为由于继续遍历只会遍历到该点的子树,故该点即为该点子树上所有的点与该点LCD的最近公共祖先.
倘若触底了,即到了一个没有在与之联通且未被访问过的节点,那么开始搜索LCD查询中与该点相关的点.倘若存在与该点相关的查询不妨设另外那个点为u.假设u被标记为已经被访问过,由于是dfs序访问,那么当前点一定是在u点的子树上,那么答案就是father[u] (因为后面讲的情况就不能采用father)
假设需要回溯,就需要将该点的father改为其父节点.因为假如再从其父节点遍历到的的与该点求LCD,那么答案就是其父节点.
附上代码:
int dfs(int x){
father[x]=x;
visit[x]=1;
for(int k=head[x];k;k=edge[k].next)
if(!visit[edge[k].to]){
dfs(edge[k].to);
father[edge[k].to]=x;
}
for(int k=qhead[x];k;k=qedge[k].next)
if(visit[qedge[k].to]){
ans=find(qedge[k].to);
}
}
3.倍增在线
上面的tarjan是离线算法,因为它需要知道所有的查询之后再通过一次dfs实现,时间复杂度比倍增快一些。而这个倍增则是在线算法,即一次查询之后直接给出一个结果
考虑一下,如果用暴力做,做法应该是将两个点调到同一高度之后不断同时向上跳,知道两点重合,该点即为两点的最近公共祖先。那么这么做的劣势就在于一次次跳太过于繁琐,导致复杂度飙升。那么倍增就是通过优化这一点而降低了复杂度。
假设需要调5次,那么5=4+1;
需要调15次? 15=8+4+2+1,
发现任意次数都可以用2的指数幂之和来表示,那么这么做的复杂度就讲到了logn.
注意一点,递加必须要从大到小,这样做可以避免以下情况。
假如是5,第一次加1,结果为1,;第二次加2,结果为3;第三次想要加4,但结果已经是7,超出了要求的5,。可以发现如果从小到大加,不知道那些需要加,那些不需要加;但是从大到小加就没有这种顾虑,只要大小满足就可以加。
倍增做法的关键变量:
-
depth[]: 如其表意,就是求一个点的深度(hint:根节点最好从0开始)
-
grand[i][j]: 指i节点向上跳2的j次方次跳到了那一个点上。
那么两个变量怎么用呢。假设当前求LCD(a,b),那么首先,我们让a和b的高度对齐,然后让两个点不断往上跳,直到重合。判断逻辑为,不断枚举2的次方的值,假如两个点跳了这个距离但不重合的情况下就跳。这样模拟到最后,两个点会止步于目标的下一个点(因为判断逻辑不允许两个点最后重合)这样,只要最后输出任意一个点向上再跳一个点即可 e.p.: grand[x][0]为x点向上跳一个点
知道了两个变量怎么用,我么就需要事先求出来两个变量的值,这样每一次询问的时候就能利用两个变量迅速输出答案,达到在线的目的。
还是dfs:对于每一个点,其depth值等于其父节点的depth值加一。(相信在dfs时传入上一个节点的值并不是难事)其grand[x][0]预设为其父节点,其余值递推出来
for(int i=1;(1<这段代码就是递推的核心语句,很重要!!
这样下来一遍,depth和grand均已知,就能很方便地求出LCD
预处理部分:
void dfs(int x,int pre){
vis[x]=true;
depth[x]=depth[pre]+1;
deep=max(deep,depth[x]);
grand[x][0]=pre;
for(int i=1;(1<查询部分:
int lca(int x,int y){
if(depth[x]=0;--i){
if(depth[x]>=depth[y]+(1<=0;--i){
if(grand[x][i]!=grand[y][i]){
x=grand[x][i];
y=grand[y][i];
}
}
return grand[x][0];
}
那么倍增算法就完事了
貌似还有一种rmq算法,有空再补坑吧