ACM计算几何篇

https://linxi99.gitee.io/20190211/ACM计算几何篇/

1 前言

1.1 计算几何算法

ACM各种算法中计算几何算是比较实际的算法，在很多领域有着重要的用途

常用算法包括经典的凸包求解，离散化及扫描线算法、旋转卡壳、半平面交等

1.2 计算几何题目特点及要领

• 大部分不会很难，少部分题目思路很巧妙

• 做计算几何题目，模板很重要，模板必须高度可靠

• 要注意代码的组织，因为计算几何的题目很容易上两百行代码，里面大部分是模板。如果代码一片混乱，那么会严重影响做题正确率。

• 注意精度控制

• 能用整数的地方尽量用整数，要想到扩大数据的方法（扩大一倍，或扩大sqrt2）。因为整数不用考虑浮点误差，而且运算比浮点快

1.3 预备知识

见ACM几何基础篇

https://linxi99.gitee.io/20190211/ACM几何基础篇/

https://blog.csdn.net/linxilinxilinxi/article/details/81750327

计算几何将用到大量基础篇中的函数与知识

2 凸包

2.1 定义

2.1.1 凸多边形

过多边形的任意一边做一条直线，如果其他各个顶点都在这条直线的同侧，则把这个多边形叫做凸多边形

凸包求解算法的基础便是凸多边形的定义与性质

2.1.2 凸包

假设平面上n个点，过某些点作一个多边形，使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候，我们就叫它“凸包”

形象理解：皮筋包裹钉子群

2.2 颜料配色问题

2.2.1 问题描述

假设每种颜料都拥有$(R,G,B)$三种属性，表示该种颜料红色，绿色，与蓝色的化学成分所占的比重

给你若干种已有的不限量的颜料，问是否能够勾兑出目标颜料$(R_0,G_0,B_0)$

2.2.2 问题简化

若只考虑$(R,G)$这两种颜色

给定$X=(10\%,35\%),Y=(16\%,20\%)$

问是否能够配制出$U=(12\%,30\%)$的燃料

$V=(13\%,22\%)$这一种呢

如果再给你一种$Z=(7\%,15\%)$颜料呢

2.2.3 问题抽象

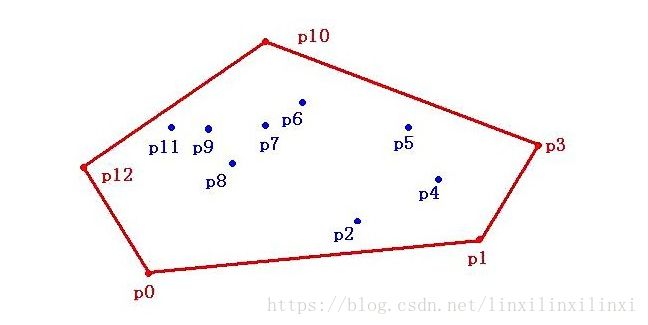
将每一种颜料映射为二维欧氏空间中的一个点，我们可以将已经给定的颜料与目的颜料在空间中标定出来

经过观察与思考，我们可以发现，一个颜料能够被勾兑出来当且仅当该颜料对应的点，位于以给定颜料所构成的凸包之中

2.2.4 数学抽象

Given a point set $S=\{p_1,\cdots ,p_n\}\subseteq {\epsilon }^2$

Let $\lambda =<{\lambda }_1,\cdots ,{\lambda }_n>\in R^n,{\lambda }_1+{\lambda }_2+\cdots +{\lambda }_n=1$ and $min\{{\lambda }_1,\cdots ,{\lambda }_n\}\ge 0$

The point

$p=[p_1,\cdots ,p_n]\lambda ={\lambda }_1{p}_1+\cdots +{\lambda }_n{p}_n$

is called a convex combination of S

2.2.4.1 Convex Combination And Affine Combination

凸组合：Convex Combination

两个点的Convex Combination会是这两个点所构成的线段

仿射组合：Affine Combination

而两个点的Affine Combination将会确定这两个点所对应的那条直线

2.2.4.2 区别与联系

也就是说Convex Combination 是 Affine Combination的一个子集

原因便是

$min\{{\lambda }_1,\cdots ,{\lambda }_n\}\ge 0$

这个根据生活实际添加的条件

2.3 构造凸包的初步尝试

2.3.1 转化思想

大事化小，小事化了

2.3.2 极性 Extremity

称最终对点集所构成的凸包有贡献的点具有极性

称其为极点 Extreme Point

通过观察，所谓的这些极点，我们可以找到一条穿过它们的直线，使得点集中的所有点都落在直线的同一侧

2.3.3 基于极点的凸包构造算法

类比冒泡排序，我们可以逐个判断每一个给定的点是否位于任何三个点所构成的三角形的内部

这样我们可以逐个剔除所有的非极点，从而得到所有的极点，即凸包的解

很容易想到，该算法的时间复杂度$O(n^4)$

2.3.4 基于极边的凸包构造算法

2.3.4.1 极边

类比极点的定义相应的我们也可以定义极边(Extreme Edge)，它们具有类似的性质

很容易可以发现凸包边界上的边若取逆时针走向，点集中所有的都位于极边的左侧(ToLeftTest)

2.3.4.2 尝试实现

枚举所有点所有边，判断其左右位置相对关系，如果所有点都落在该边的某一侧，则该边为极边，其端点为极点

易得，时间复杂度为$O(n^3)$

2.4 更进一步

2.4.1 减而治之

类比插入排序

我们可以考虑根据之前数据已经构成一个凸包，当新点来临之后，我们便可以考虑当前的点是否位于多边形内部 isPointInPolygon()

若位于内部或边界之上，我们便可以断定该点对凸包没有贡献

否则，将该点与凸包所构成的两条支撑线(Support-Lines)缝合到已有答案集合之中，并舍弃失去极性的点

2.4.2 转向形式

Pattern Of Turns

利用每个顶点相对于当前试图加入的点的不同的转向形式，获得支撑线以及不被丢弃的所有点

2.4.3 优点与劣势

该算法为在线算法，可以动态的添加点，从而改变凸包形式

但其复杂度虽然达到了$O(n^2)$，但还是不尽如人意

2.5 求解凸包的高效算法

2.5.1 Jarvis March的步进算法

类比选择排序

2.5.1.1 思路分析

Lowest-Then-Leftmost

纵坐标最小然后横坐标最小的点一定是凸包上的点， 我们将其记为$p_0$

从 $p_0$ 开始，按逆时针的方向，逐个找凸包上的点，每前进一步找到一个点，所以叫作步进法。

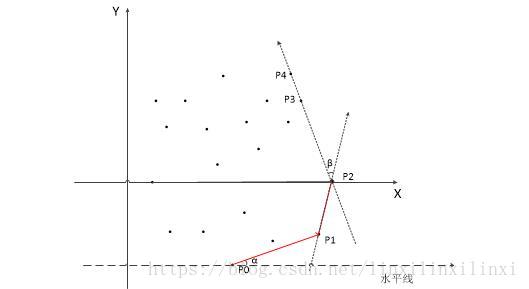
怎么找下一个点呢？利用夹角。假设现在已经找到 $\{p_0，p_1，p_2\}$ 了

要找下一个点：剩下的点分别和 $p_2$ 组成向量，设这个向量与向量$p_1{p}_2$的夹角为$\beta$。

当 $\beta$ 最小时就是所要求的下一个点了

2.5.1.2 时间复杂度

$O(nH)$。（其中 n 是点的总个数，H 是凸包上的点的个数）

具有输出敏感性，所花费的时间与输出的凸包的顶点个数有关

2.5.1.3 注意

找第二个点 $p_1$ 时，因为已经找到的只有 $p_0$ 一个点，所以向量只能和水平线作夹角 $\alpha$，当 $\alpha$ 最小时求得第二个点

共线情况：如果直线 $p_2{p}_3$ 上还有一个点 $p_4$，即三个点共线

此时由向量$p_2{p}_3$ 和向量 $p_2{p}_4$ 产生的两个 $\beta$ 是相同的

我们应该把 $p_3$、$p_4$ 都当做凸包上的点

并且把距离 $p_2$ 最远的那个点作为最后搜索到的点，继续找它的下一个连接点

2.5.2 Graham Scan

2.5.2.1 预处理

Graham扫描的思想和Jarvis步进法类似，也是先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，但它不是利用夹角。

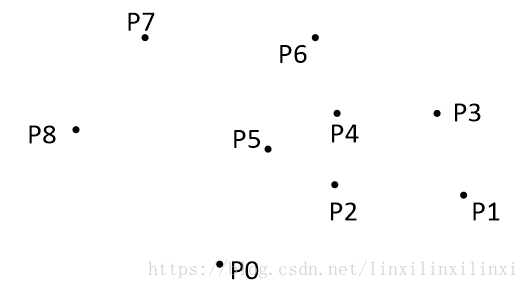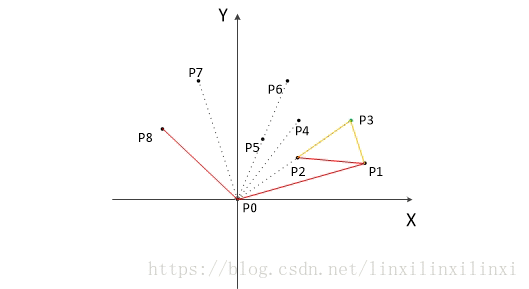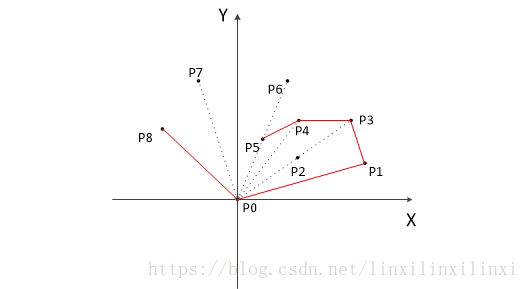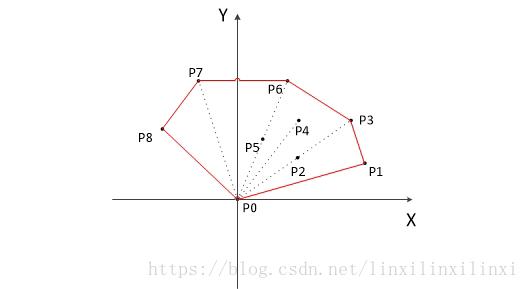
把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的$p_0$。

把所有点的坐标平移一下，使 $p_0$ 作为原点，如上图。

2.5.2.2 具体步骤

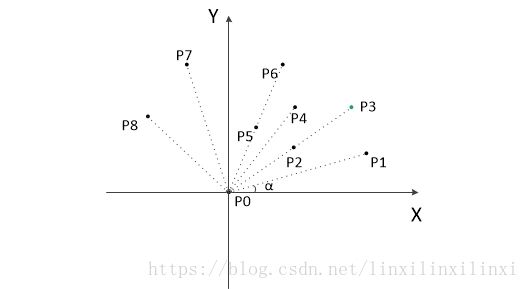
1. 计算各个点相对于 $p_0$ 的幅角 $\alpha$ ，按从小到大的顺序对各个点排序。

2. 当 $\alpha$ 相同时，距离 $p_0$ 比较近的排在前面。例如上图得到的结果为 $p_1$，$p_2$，$p_3$，$p_4$，$p_5$，$p_6$，$p_7$，$p_8$。

3. 我们由几何知识可以知道，结果中第一个点 $p_1$ 和最后一个点 $p_8$ 一定是凸包上的点。
   （以上是准备步骤，以下开始求凸包）
   以上，我们已经知道了凸包上的第一个点 $p_0$ 和第二个点 $p_1$，我们把它们放在栈里面。
   现在从按照极角排好的集合里，把 $p_1$ 后面的那个点拿出来做当前点，即 $p_2$ 。接下来开始找第三个点：

4. 连接栈顶的点与次栈顶的点，得到直线 $l$ 。看当前点是在直线 $l$ 的右边还是左边。
   如果在直线的右边就执行步骤5；
   如果在直线上，或者在直线的左边就执行步骤6。

5. 如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。

6. 当前点是凸包上的点，把它压入栈，执行步骤7。

7. 检查当前的点 $p_i$ 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 $p_i$ 后面那个点做当前点，返回步骤4。

最后，栈中的元素就是凸包上的点了。

以下为用 GrahamScan 动态求解的过程：

大家可以直观的了解一下

2.5.2.3 时间复杂度

根据Scan过程的步骤分析，我们可以得到其时间复杂度为$O(n)$

但由于其预处理排序时间复杂度为$O(nlogn)$

故其总的时间复杂度为$O(nlogn)$

2.5.2.4 代码实现

根据实现难度，对上述步骤做了些许修改

const int maxn = 1e3 + 5;
struct Point {
    double x, y;
    Point(double x = 0, double y = 0):x(x),y(y){}
};
typedef Point Vector;
Point lst[maxn];
int stk[maxn], top;
Vector operator - (Point A, Point B){
    return Vector(A.x-B.x, A.y-B.y);
}
int sgn(double x){
    if(fabs(x) < eps)
        return 0;
    if(x < 0)
        return -1;
    return 1;
}
double Cross(Vector v0, Vector v1) {
    return v0.x*v1.y - v1.x*v0.y;
}
double Dis(Point p1, Point p2) { //计算 p1p2的 距离
    return sqrt((p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y));
}
bool cmp(Point p1, Point p2) { //极角排序函数 ，角度相同则距离小的在前面
    int tmp = sgn(Cross(p1 - lst[0], p2 - lst[0]));
    if(tmp > 0)
        return true;
    if(tmp == 0 && Dis(lst[0], p1) < Dis(lst[0], p2))
        return true;
    return false;
}
//点的编号0 ~ n - 1
//返回凸包结果stk[0 ~ top - 1]为凸包的编号
void Graham(int n) {
    int k = 0;
    Point p0;
    p0.x = lst[0].x;
    p0.y = lst[0].y;
    for(int i = 1; i < n; ++i) {
        if( (p0.y > lst[i].y) || ((p0.y == lst[i].y) && (p0.x > lst[i].x)) ) {
            p0.x = lst[i].x;
            p0.y = lst[i].y;
            k = i;
        }
    }
    lst[k] = lst[0];
    lst[0] = p0;
    sort(lst + 1, lst + n, cmp);
    if(n == 1) {
        top = 1;
        stk[0] = 0;
        return ;
    }
    if(n == 2) {
        top = 2;
        stk[0] = 0;
        stk[1] = 1;
        return ;
    }
    stk[0] = 0;
    stk[1] = 1;
    top = 2;
    for(int i = 2; i < n; ++i) {
        while(top > 1 && Cross(lst[stk[top - 1]] - lst[stk[top - 2]], lst[i] - lst[stk[top - 2]]) <= 0)
            --top;
        stk[top] = i;
        ++top;
    }
    return ;
}

2.5.3 Andrew算法

2.5.3.1 由来

Andrew算法是GrahamScan算法的变种

和原始的GrahamScan算法相比，Andrew更快，且数值稳定性更好

2.5.3.2 预处理

基于水平排序

首先把所有点按照 Leftmost Then Lowest 原则排序，删除重复点后得到序列$p_1,p_2\cdots$

然后把$p_1$和$p_2$放到凸包中。

2.5.3.3 算法步骤

从$p_3$开始，当新点在凸包的“前进”方向的左边时继续，否则依次删除最近加入凸包的点，直到新点在左边

重复此过程，直到碰到最右边的$p_n$，就求出了“下凸包”。然后反过来从$p_n$开始再做一次，求出“上凸包”，合并起来就是完整的凸包

2.5.3.4 时间复杂度

两次扫描均为$O(n)$

预处理排序的时间复杂度为$O(nlogn)$

总时间复杂度为$O(nlogn)$

2.5.3.5 代码实现

struct Point {
    double x, y;
    Point(double x = 0, double y = 0):x(x),y(y){}
};
typedef Point Vector;
Vector operator - (Point A, Point B){
    return Vector(A.x-B.x, A.y-B.y);
}
bool operator < (const Point& a, const Point& b){
    if(a.x == b.x)
        return a.y < b.y;
    return a.x < b.x;
}
double Cross(Vector v0, Vector v1) {
    return v0.x*v1.y - v1.x*v0.y;
}
//计算凸包，输入点数组为 p，个数为 n， 输出点数组为 ch。函数返回凸包顶点数
//如果不希望凸包的边上有输入点，则把两个 <= 改为 <
//在精度要求高时建议用dcmp比较
//输入不能有重复点，函数执行完后输入点的顺序被破坏
int ConvexHull(Point* p, int n, Point* ch) {
    sort(p, p+n);
    int m = 0;
    for(int i = 0; i < n; ++i) {
        while(m > 1 && Cross(ch[m-1] - ch[m-2], p[i] - ch[m-2]) < 0) {
            m--;
        }
        ch[m++] = p[i];
    }
    int k = m;
    for(int i = n-2; i>= 0; --i) {
        while(m > k && Cross(ch[m-1] - ch[m-2], p[i] - ch[m-2]) < 0) {
            m--;
        }
        ch[m++] = p[i];
    }
    if(n > 1)
        --m;
    return m;
}

2.5.4 分治法求解凸包

2.5.5 Melkman算法

3 离散化

3.1 概述

与其说离散化是一种算法，不如说是一种程序设计中的非常常用的技巧，它可以有效的降低时间复杂度

离散化不仅在计算几何中经常用到，它几乎和所有算法都能结合成为考点

3.2 基本思想

在众多可能的情况中只考虑我需要用的值

3.3 例题：区域的个数

3.3.1 题目描述

$w\times h$ 的的格子画了$n$条或垂直或水平宽度为1的直线，求出这些格子被划分成了多少个4连块（上、下、左、右连通）。

【输入格式】

第一行包含两个整数：w和h，表示矩形的列数和行数（行列编号都从1开始）。
　　第二行包含一个整数n，表示有n条直线。
　　接下来的n行，每行包含四个整数：x1,y1,x2,y2，表示一条直线的列号和行号。

【输出格式】

一个整数，表示区域数量。

【输入样例】

10 10
5
1 4 6 4
1 8 10 8
4 1 4 10
9 1 9 5
10 6 10 10

【输出样例】

6

【数据范围】

1<=w,h<=1000000 , 1<=n<=500

3.3.2 思路分析

准备好$w\times h$的数组，并记录是否有直线通过，然后一通$bfs$或者$dfs$就可以解决战斗

但这个问题中$w$和$h$最大为1000000，所以没有办法创建$w\times h$的数组

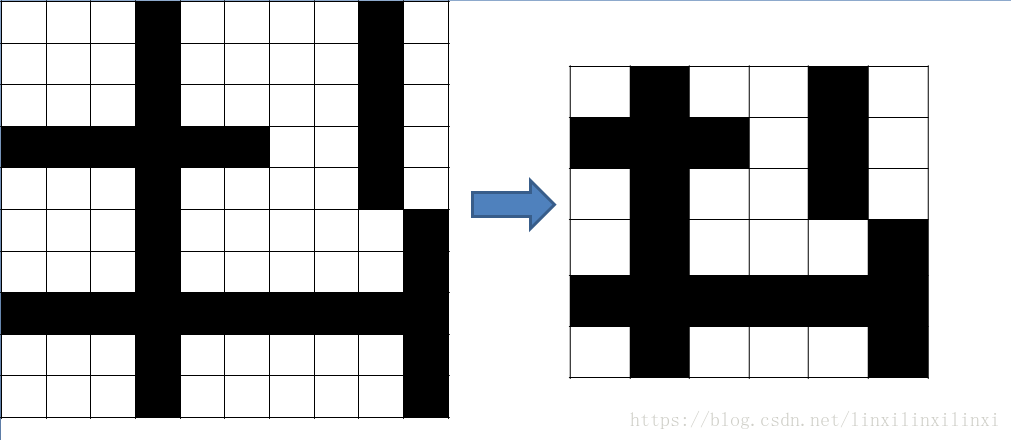
因此我们需要使用坐标离散化这一技巧

如上图所示，将前后没有变化的行列消除后并不会影响区域的个数

数组里只需要存储有直线的行列以及其前后的行列就足够了，这样的话大小最多$6n\times 6n$，因此就可以创建出数组并利用搜索求出区域的个数

3.3.3 代码实现

#include 
using namespace std;
const int maxn = 5e2 + 5;
int x1[maxn], x2[maxn], y1[maxn], y2[maxn];//开始列号结束列号，开始行号，结束行号
int w, h, n, ans;//宽，高，以及横线的个数
bool line[maxn*6][maxn*6];
int dire[5][3]= {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
struct node {
    int x, y;
    node(int x, int y):x(x), y(y) {}
};
//对x1和x2进行离散化，并返回离散化之后的宽度
int compress(int *xx1,int *xx2,int w) { //开始坐标，结束坐标
    vector<int> v;
    for(int i = 0; i < n; ++i) //将横线本身以及附近两横线存储
        for(int d = -1; d <= 1; ++d) {
            int nx1 = xx1[i] + d;
            int nx2 = xx2[i] + d;
            if(nx1 >= 1 && nx1 <= w) v.push_back(nx1);
            if(nx2 >= 1 && nx2 <= w) v.push_back(nx2);
        }
    //去重
    sort(v.begin(), v.end());
    v.erase(unique(v.begin(),v.end()),v.end());
    //unique()函数去重并返回多余元素存储的起始位置
    //erase()函数区间删除左开右闭的区间
    //离散化后的坐标
    for(int i = 0; i < n; ++i) {
        xx1[i] = find(v.begin(), v.end(), xx1[i]) - v.begin();
        xx2[i] = find(v.begin(), v.end(), xx2[i]) - v.begin();
        //通过find()函数将坐标转化为了下标
    }
    return v.size();
}

void bfs(int xx,int yy) {
    queue<node> q;
    q.push(node{xx, yy});
    line[xx][yy] = 1;

    while(!q.empty()) {
        node t=q.front();
        q.pop();
        int x=t.x;
        int y=t.y;

        for(int i=0; i<4; i++) {
            int nx=x+dire[i][0];
            int ny=y+dire[i][1];
            if(nx<0||nx>=h||ny<0||ny>=w)continue;
            if(!line[nx][ny]) {
                line[nx][ny]=1;
                q.push(node(nx, ny));
            }
        }
    }
    return ;
}
int main() {
    while(cin >> w >> h >> n) {
        ans = 0;
        memset(line, false, sizeof(line));

        for(int i = 0; i < n; ++i) cin >> x1[i];
        for(int i = 0; i < n; ++i) cin >> x2[i];
        for(int i = 0; i < n; ++i) cin >> y1[i];
        for(int i = 0; i < n; ++i) cin >> y2[i];

        w = compress(x1, x2, w);
        h = compress(y1, y2, h);

        //标记上所在横线上的点
        for(int i = 0; i < n; ++i) //枚举n条横线
            for(int y = y1[i]; y <= y2[i]; ++y) //枚举行
                for(int x = x1[i]; x <= x2[i]; ++x) //枚举列
                    line[y][x] = true;

        //打印查看离散化后的图形
        /*
        for(int i=0;i
        //搜索求区域块数 防止爆栈，这里使用广搜
        for(int i = 0; i < h; ++i){
            for(int j = 0; j < w; ++j) {
                if(!line[i][j]) {
                    ++ans;
                    bfs(i,j);
                }
            }
        }
        cout<<ans<<endl;
    }

    return 0;
}
/*
10 10 5
1 1 4 9 10
6 10 4 9 10
4 8 1 1 6
4 8 10 5 10
*/

4 扫描线法（平面扫描）

4.1 描述

在集合问题中，我们经常利用平面扫描技术来降低算法的复杂度

所谓平面扫描，是指扫描线在平面上按给定轨迹移动的同时，不断根据扫描线扫过部分更新信息，从而得到整体所要求的结果的方法

扫描的方法，既可以从左向右与$y$轴平行的直线，也可以固定射线的端点逆时针转动

4.2 例题：矩形面积并

4.2.1 题目描述

给出$n$个矩形的左下角和右上角的坐标，求矩形面积的并

【输入格式】

第一行包含一个整数：n，表示矩形数量。
　　第$2$到$n+1$行，每行包含四个浮点数，表示该矩形左下角与右上角的坐标

【输出格式】

矩形面积交的大小

【输入样例】
　　2
　　10 10 20 20
　　5 15 25 25.5
【输出样例】

180.00

【数据范围】

1 <= n <= 100
0 <= x1 < x2 <= 100000，0 <= y1 < y2 <= 100000

4.2.2 思路分析

首先，矩形比较多，坐标也很大，所以横坐标需要离散化（纵坐标不需要离散化）

//不离散化直接线段树维护也可以

考虑一条扫描线，从最下方竖直向上扫描

扫描前我们需要保存好矩形的上下边，并且按照高度进行排序，

另外如果该边为矩形的上边则将其标记为-1

否则将其标记为1

接着让扫描线从下往上扫描，每遇到一条上下边就停下来，将这条线段投影到总区间上

这个投影对应的其实就是插入和删除线段的操作

下边是1，扫描到下边的话相当于往总区间插入一条线段

上边是-1，扫描到上边的话相当于在总区间删除一条线段

每次扫描到一条上下边后，就区间求和，得到现在被覆盖的总长度，乘其扫过的高度并将其统计起来

以此往复，当扫出最高的那条边，我们便获得了所需求得矩形面积交

4.3 寻找平面线段交点O(nlogn)

5 半平面交

5.1 描述

简单地说，半平面交问题就是给出若干个半平面，求他们的公共部分。

其中每个半平面都用一条有向线段表示，它的左侧就是它所代表的半平面

5.2 有向线段

代码实现

struct Line{
    Point p;//直线上任意一点
    Vector v;//方向向量，它的左边就是对应的半平面
    double ang;//极角，即从x轴正半轴旋转到向量v所需要的角（弧度）
    Line(){}
    Line(Point p, Vector v) : p(p), v(v){
        ang = atan2(v.y, v.x);
    }
    bool operator < (const Line& L) const {//排序用的比较运算符
        return ang < L.ang;
    }
};

5.3 半平面交的结果

在很多情况下，半平面交的结果都是一个凸多边形

但也有时候会得到一个无界多边形

甚至是一条直线、线段或者是点

但不管怎样，结果一定是凸的（凸集的交是凸的）

当然，半平面交也可以为空

5.4 计算方法

5.4.1 增量法

初始答案为整个平面

然后逐一的加入各个半平面，维护当前的半平面交

为了编程方便，我们一般用一个很大的矩形（4个半平面的交）代替“整个平面”

计算出结果以后再删去这四个人工半平面

这样，没加入一个平面就相当于用一条有向直线去切割多边形

5.4.2 切割方法

按照逆时针顺序考虑多边形所有的顶点

保留在直线左侧和直线上的点，而删除直线右边的点

如果有向直线和多边形相交时产生了新的点，这些点应该加在新的多边形中

5.4.3 时间复杂度

每次遍历切割的时间复杂度为$O(n)$

但我们可以通过双端队列优化加扫描的方式将每次切割的成本平摊为$O(logn)$

因此半平面交可以在$O(nlogn)$的时间内解决

5.4.4 代码实现

const double eps = 1e-6;
struct Point{
    double x, y;
    Point(double x = 0, double y = 0):x(x),y(y){}
};
typedef Point Vector;
Vector operator + (Vector A, Vector B){
    return Vector(A.x+B.x, A.y+B.y);
}
Vector operator - (Point A, Point B){
    return Vector(A.x-B.x, A.y-B.y);
}
Vector operator * (Vector A, double p){
    return Vector(A.x*p, A.y*p);
}
int sgn(double x){
    if(fabs(x) < eps)
        return 0;
    if(x < 0)
        return -1;
    return 1;
}
double Dot(Vector A, Vector B){
    return A.x*B.x + A.y*B.y;
}
double Cross(Vector A, Vector B){
    return A.x*B.y-A.y*B.x;
}
double Length(Vector A){
    return sqrt(Dot(A, A));
}
Vector Normal(Vector A){//向量A左转90°的单位法向量
    double L = Length(A);
    return Vector(-A.y/L, A.x/L);
}
struct Line{
    Point p;//直线上任意一点
    Vector v;//方向向量，它的左边就是对应的半平面
    double ang;//极角，即从x轴正半轴旋转到向量v所需要的角（弧度）
    Line(){}
    Line(Point p, Vector v) : p(p), v(v){
        ang = atan2(v.y, v.x);
    }
    bool operator < (const Line& L) const {//排序用的比较运算符
        return ang < L.ang;
    }
};
//点p在有向直线L的左侧
bool OnLeft(Line L, Point p){
    return Cross(L.v, p - L.p) > 0;
}
//两直线交点。假定交点唯一存在
Point GetIntersection(Line a, Line b){
    Vector u = a.p - b.p;
    double t = Cross(b.v, u)/Cross(a.v, b.v);
    return a.p + a.v*t;
}
//半平面交的主过程
int HalfplaneIntersection(Line* L, int n, Point* poly){
    sort(L, L + n);//按照极角排序
    int fst = 0, lst = 0;//双端队列的第一个元素和最后一个元素
    Point *P = new Point[n];//p[i] 为 q[i]与q[i + 1]的交点
    Line *q = new Line[n];//双端队列
    q[fst = lst = 0] = L[0];//初始化为只有一个半平面L[0]
    for(int i = 1; i < n; ++i){
        while(fst < lst && !OnLeft(L[i], P[lst - 1])) --lst;
        while(fst < lst && !OnLeft(L[i], P[fst])) ++fst;
        q[++lst] = L[i];
        if(sgn(Cross(q[lst].v, q[lst - 1].v)) == 0){
            //两向量平行且同向，取内侧一个
            --lst;
            if(OnLeft(q[lst], L[i].p)) q[lst] = L[i];
        }
        if(fst < lst)
            P[lst - 1] = GetIntersection(q[lst - 1], q[lst]);
    }
    while(fst < lst && !OnLeft(q[fst], P[lst - 1])) --lst;
    //删除无用平面
    if(lst - fst <= 1) return 0;//空集
    P[lst] = GetIntersection(q[lst], q[fst]);//计算首尾两个半平面的交点
    //从deque复制到输出中
    int m = 0;
    for(int i = fst; i <= lst; ++i) poly[m++] = P[i];
    return m;
}

6 分治法解决平面最近点对（O(nlogn)）

const int maxn = 2e5 + 5;
const double inf = 1e10;

struct Point {
    double x,y;
    bool operator <(const Point &a)const {
        return x < a.x;
    }
};

inline double dist(const Point &p1, const Point &p2) {
    return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}

Point p[maxn], q[maxn];
double ClosestPair(int l, int r) {
    if(l == r)
        return inf;
    int mid = (l+r)>>1;
    double tx = p[mid].x;
    int tot = 0;
    double ret = min(ClosestPair(l, mid), ClosestPair(mid + 1, r));
    for(int i = l, j = mid + 1; (i <= mid || j <= r); ++i) {
        while(j <= r && (p[i].y > p[j].y || i > mid)) {
            q[tot++] = p[j];
            j++; //归并按y排序
        }
        if(abs(p[i].x - tx) < ret && i <= mid) { //选择中间符合要求的点
            for(int k = j - 1; k > mid && j - k < 3; --k)
                ret = min(ret, dist(p[i], p[k]));
            for(int k = j; k <= r && k-j < 2; ++k)
                ret = min(ret, dist(p[i], p[k]));
        }
        if(i <= mid)
            q[tot++] = p[i];
    }
    for(int i = l, j = 0; i <= r; ++i, ++j)
        p[i] = q[j];
    return ret;
}

7 旋转卡壳（O(nlogn)解决平面最远点对）

double Dist2(Point p1, Point p2) { //计算距离的平方
    double ret = Dot(p1 - p2, p1 - p2);
    return ret;
}
double RotatingCalipers(Point* ch, int m) {//返回平面最大距离的平方
    if(m == 1) return 0.0;
    if(m == 2) return Dist2(ch[0], ch[1]);
    double ret = 0.0;
    ch[m] = ch[0];
    int j = 2;
    for(int i = 0; i < m; ++i) {
        while(Cross(ch[i + 1] - ch[i], ch[j] - ch[i]) < Cross(ch[i + 1] - ch[i], ch[j + 1] - ch[i]))
            j = (j + 1)%m;
        ret = max(ret, max(Dist2(ch[j], ch[i]), Dist2(ch[j], ch[i + 1])));
    }
    return ret;
}

8 三点确定外接圆圆心坐标

struct Point {
    double x,y;
    Point(double x = 0, double y = 0):x(x),y(y){}
};
Point Excenter(Point a, Point b, Point c){
    double a1 = b.x - a.x;
    double b1 = b.y - a.y;
    double c1 = (a1*a1 + b1*b1)/2;
    double a2 = c.x - a.x;
    double b2 = c.y - a.y;
    double c2 = (a2*a2 + b2*b2)/2;
    double d = a1*b2 - a2*b1;
    return Point(a.x + (c1*b2 - c2*b1)/d, a.y + (a1*c2 - a2*c1)/d);
}