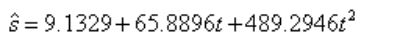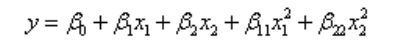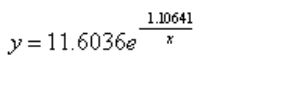数据回归分析和拟合的Matlab实现
本次教程的主要内容包含：
一、多元线性回归
多元线性回归：regress
二、多项式回归
一元多项式：polyfit或者polytoo l
多元二项式：rstool或者rsmdemo
三、非线性回归
非线性回归：nlinfit
四、逐步回归
逐步回归：stepwise
一、多元线性回归
多元线性回归：
1、b=regress(Y, X )
确定回归系数的点估计值
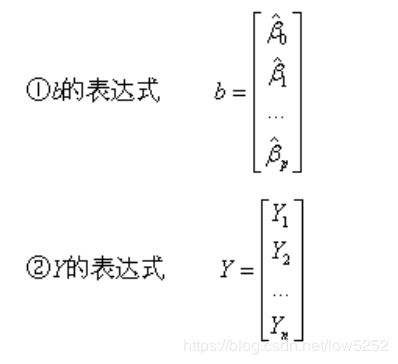
2、[b, bint,r,rint,stats]=regress(Y,X,alpha)
求回归系数的点估计和区间估计、并检验回归模型
①bint表示回归系数的区间估计.
②r表示残差
③rint表示置信区间
④stats表示用于检验回归模型的统计量,有三个数值：相关系数r2、F值、与F对应的概率p
说明：相关系数r2越接近1，说明回归方程越显著；
F>F(1-a)[k,k-n-1]时拒绝H0，F越大，说明回归方程越显著；
与F对应的概率p<α时拒绝H0
⑤alpha表示显著性水平(缺省时为0.05)
3、rcoplot(r,rint)
画出残差及其置信区间
具体参见下面的实例演示
4、实例演示，函数使用说明
(1)输入数据复制内容到剪贴板代码:
>>x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
>>X=[ones(16,1) x];
>>Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';
(2)回归分析及检验复制内容到剪贴板代码:
>> [b,bint,r,rint,stats]=regress(Y,X)
b = -16.0730
0.7194
bint = -33.7071 1.5612
0.6047 0.8340
r = 1.2056
-3.2331
-0.9524
1.3282
0.8895
1.1702
-0.9879
0.2927
0.5734
1.8540
0.1347
-1.5847
-0.3040
-0.0234
-0.4621
0.0992
rint =
-1.2407 3.6520
-5.0622 -1.4040
-3.5894 1.6845
-1.2895 3.9459
-1.8519 3.6309
-1.5552 3.8955
-3.7713 1.7955
-2.5473 3.1328
-2.2471 3.3939
-0.7540 4.4621
-2.6814 2.9508
-4.2188 1.0494
-3.0710 2.4630
-2.7661 2.7193
-3.1133 2.1892
-2.4640 2.6624
stats =
0.9282 180.9531 0.0000 1.7437
运行结果解读如下参数回归结果为，
对应的置信区间分别为[-33.7017,1.5612]和[0.6047,0.834];
r2=0.9282(越接近于1，回归效果越显著)，F=180.9531，p=0.0000，由p<0.05, 可知回归模型
y=-16.073+0.7194x
成立
(3)残差分析
作残差图 rcoplot(r,rint)
二、多项式回归
一元多项式回归
1、一元多项式回归函数
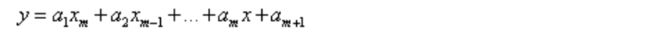
(1)[p,S]= pol yfit(x,y,m) 确定多项式系数的matlab命令说明：
x=(x1,x2,...,xn),y=(y1,y2,...,yn)；
p=(a1,a2,...,am+1)是多项式y=a1xm+a2xm-1+...+amx+am+1的系数；
S是一个矩阵,用来估计预测误差
(2)polytool(x,y,m) 调用多项式回归GUI界面，参数意义同polyfit
2、预测和预测误差估计
(1)Y=pol yval(p,x) 求pol yfit所得的回归多项式在x处的预测值Y
(2)[Y,DELTA]=polyco nf(p,x,S,alpha)求polyfit所得的回归多项式在x处的预测值Y及预测值的显著性为1-alpha的置信区间Y ±DELTA，alpha缺省时为0. 5
3、实例演示说明
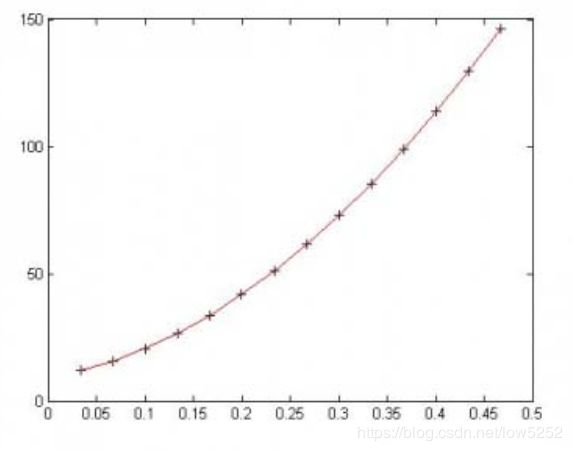
观测物体降落的距离s与时间t的关系，得到数据如下表，求s的表达式 (即回归方程s=a+bt+ct^2)
t (s) 1 /30 2/3 0 3/30 4/30 5/30 6 /30 7 /30
s (cm) 11.86 15.67 20.60 26.69 33.71 41.93 51.13
t (s) 8 /30 9/3 0 10/3 0 11/3 0 12/30 13/30 14/30
s (cm) 61.49 72.90 85.44 99.08 113.77 129.54 14 6.48
解法一：直接作二次多项式回归
>>t=1/30:1/30:14/30;
>>s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
>>[p,S]=polyfit(t,s,2)
>>p = 489.2946 65.8896 9.1329
S =
R: [3x3 double]
df: 11
normr: 0.1157
故回归模型为
解法二：化为多元线性回归
>>t=1/30:1/30:14/30;
>>s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
>>T=[ones(14,1) t' (t.^2)'];
>>[b,bint,r,rint,stats]=regress(s',T)
b =
9.1329
65.8896
489.2946
bint =
9.0614 9.2044
65.2316 66.5476
488.0146 490.5747
r =
-0.0129
-0.0302
-0.0148
0.0732
0.0040
0.0474
-0.0165
-0.0078
-0.0363
-0.0222
0.0046
-0.0059
-0.0237
0.0411
rint =
-0.0697 0.0439
-0.0956 0.0352
-0.0876 0.0580
0.0182 0.1283
-0.0709 0.0789
-0.0192 0.1139
-0.0894 0.0563
-0.0813 0.0658
-0.1062 0.0335
-0.0955 0.0511
-0.0704 0.0796
-0.0793 0.0675
-0.0904 0.0429
-0.0088 0.0910
stats = 1.0e+007 *
0.0000 1.0378 0 0.0000
故回归模型为：
预测及作图:
Y=polyconf(p,t,S)；
plot(t,s,'k+',t,Y,'r')
多元二项式回归
1、多元二项式回归Matlab命令
rstool(x,y,'model',alpha)输入参数说明：
x：n*m矩阵
；Y：n维列向量；
alpha：显著性水平(缺省时为0.05)；
mode：由下列4个模型中选择1个(用字符串输入,缺省时为线性模型)
2、实例演示说明
设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为1000、价格为6时的商品需求量
需求量100 75 80 70 50 65 9 0 100 110 60
收入1000 600 12 00 500 30 0 400 130 0 1100 13 00 300
价格5 7 6 6 8 7 5 4 3 9
解法一：选择纯二次模型
%直接用多元二项式回归如下
x1=[1000 600 1200 500 300 400 1300 1100 1300 300];
x2=[5 7 6 6 8 7 5 4 3 9];y=[100 75 80 70 50 65 90 100 110 60]';
x=[x1' x2'];
rstool(x,y,'purequadratic')
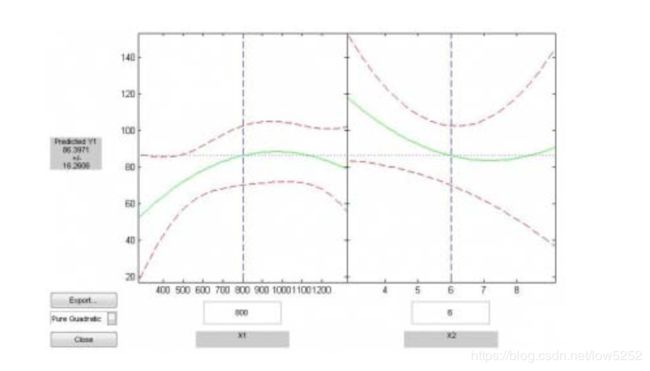
在x1对应的文本框中输入1000，X2中输入6，敲回车键，此时图形和相关数据会自动更新此时在G UI左边的“Predicted Y1”下方的数据变为88.47981，表示平均收入为1000、价格为6时商品需求量为88.4791
点击左下角的Export按钮，将会导出回归的相关参数beta、rmse和residuals到工作空间(workspace)
在Export按钮下面可以选择回归类型
在Matlab命令窗口中输入
>>beta,rmse
>将得到如下结果
beta =
110.5313
0.1464
-26.5709
-0.0001
1.8475
rmse =
4.5362
故回归模型为
解法二：
将上面模型转换为多元线性回归:
>>X=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)'];
>>[b,bint,r,rint,stats]=regress(y,X);
>>b,stats
b =
110.5313
0.1464
-26.5709
-0.0001
1.8475
stats =
0.9702 40.6656 0.0005 20.5771
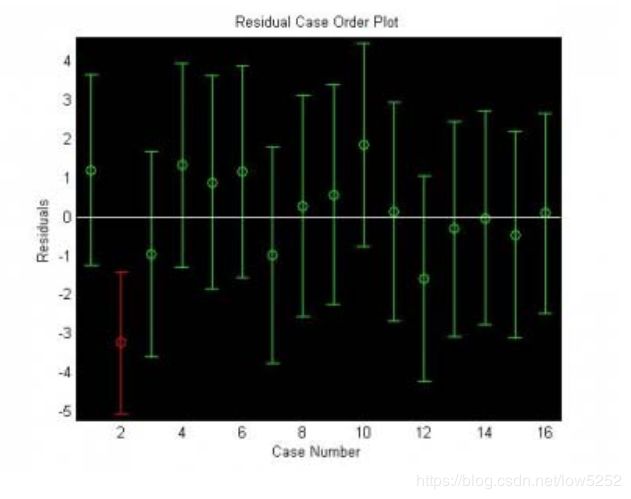
从残差图可以看出，除第二个数据外,其余数据的残差离零点均较近，且残差的置信区间均包含零点，这说明回归模型y=-16.073+0.7194x能较好的符合原始数据，而第二个数据可视为异常点。
(4)预测及作图
z=b(1)+b(2)*xplot(x,Y,'k+',x,z,'r')
三、非线性回归
1、非线性回归
[beta,r,J]=nlinfit(x,y,'modelfun ', beta0)非线性回归系数的命令
nlintool(x,y,'modelfun', beta0,alpha)非线性回归GUI界面
参数说明
beta：估计出的回归系数；
r：残差；
J：Jacobian矩阵；
x,y：输入数据x、y分别为矩阵和n维列向量，对一元非线性回归,x为n维列向量；modelfun：M函数、匿名函数或inline函数，定义的非线性回归函数；
beta0：回归系数的初值；
2、预测和预测误差估计
[Y,DELTA]=nlpredci('mo delf un', x,beta,r,J)
获取x处的预测值Y及预测值的显著性为1-alpha的置信区间Y ±D ELTA
3、实例演示说明解：
(1)对将要拟合的非线性模型，建立M函数如下
function yhat=modelfun(beta,x)
%beta是需要回归的参数
%x是提供的数据
yhat=beta(1)*exp(beta(2)./x);
(2)输入数据
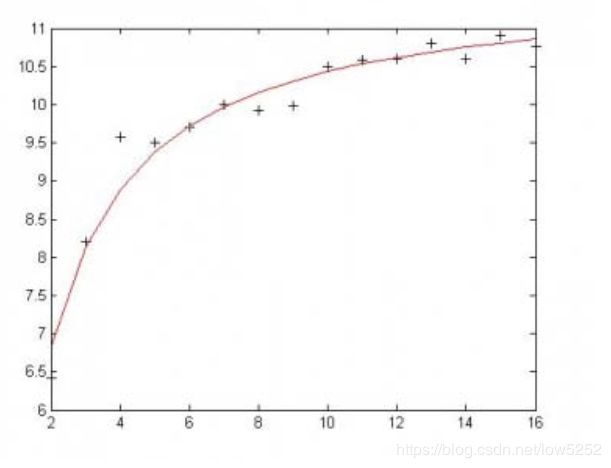
x=2:16;
y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];
beta0=[8 2]';
(3)求回归系数:
[beta,r ,J]=nlinfit(x',y',@modelfun,beta0);
beta
beta =
11.6036
-1.0641
即得回归模型为
(4)预测及作图
[YY,delta]=nlpredci('modelfun',x',beta,r ,J);
plot(x,y,'k+',x,YY,'r')
四、逐步回归
1、逐步回归的命令
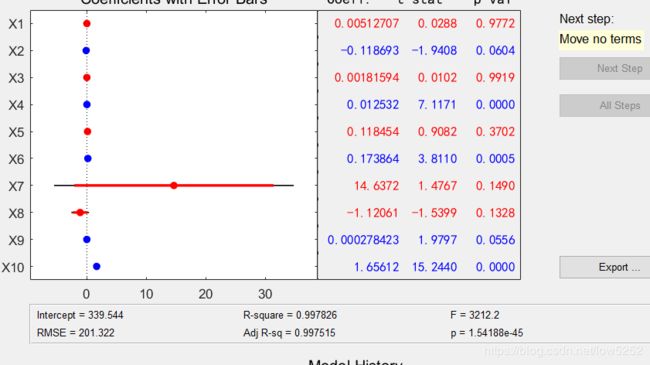
stepwise(x,y,inmodel,alpha) 根据数据进行分步回归
stepwise 直接调出分步回归GUI界面输入
参数说明:
x：自变量数据n阶矩阵；
y：因变量数据,n阶矩阵；
inmodel：矩阵的列数的指标,给出初始模型中包括的子集(缺省时设定为全部自变量)；
alpha：显著性水平(缺省时为0.5)；
2、实例演示
分析水泥凝固时放出的热量y与水泥中4种化学成分x1、x2、x3、 x4有关，今测得一组数据如下，试用逐步回归法确定一个线性模型序号
1 2 3 4 5 6 7 8 9 10 11 12 13x1 7 1 11 11 7 11 3 1 2 21 1 11 10x2 26 29 56 31 52 55 71 31 54 47 40 66 68x3 6 15 8 8 6 9 17 22 18 4 23 9 8 x4 60 52 20 47 33 22 6 44 22 26 34 12 12y 78.5 74.3 104.3 87.6 95.9 109.2 10 2.7 72.5 93.1 115.9 83.8 1 13.3 109.4
(1)数据输入
x1=[7 1 11 11 7 11 3 1 2 21 1 11 10]';
x2=[26 29 56 31 52 55 71 31 54 47 40 66 68]';
x3=[6 15 8 8 6 9 17 22 18 4 23 9 8]';
x4=[60 52 20 47 33 22 6 44 22 26 34 12 12]';
y=[78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4]';
x=[x1 x2 x3 x4];
(2)逐步回归
①先在初始模型中取全部自变量
stepwise(x,y)
