算法设计与分析基础(python实现)-- 1
欧几里得算法求最大公约数:
其方法就是重复应用下列等式,知道m mod n等于0:
gcd(m,n) = gcd(n,m mod n)
python代码
def gdc(m, n):
if n == 0:
return m
else:
tmp = m
m = n
n = tmp%n
print('gdc({},{})'.format(m,n))
return gdc(m,n)
if __name__ == "__main__":
m = input('first number:')
n = input('second number:')
value = gdc(int(m), int(n))
print('gdc value is {}'.format(value))
斐波那切数列(递归与非递归方法)
fib1.py
def fib(n):
if n<=1:
return n
else:
return fib(n-1)+fib(n-2)
if __name__ == "__main__":
n = int(input('input a number:'))
sum = fib(n)
print('Fib value is {}'.format(sum))
fib2.py
def fib(n):
num1 = 0
num2 = 1
for i in range(1,n):
fibnum = num1 + num2
num1 = num2
num2 = fibnum
return fibnum
if __name__ =="__main__":
num = int(input('input a num:'))
fibnum = fib(10)
print('Fib value is:{}'.format(fibnum))
蛮力法:
选择排序
def selection_sort(c_list):
length = len(c_list)
for i in range(length-1):
t_list = c_list[i:]
print(t_list)
min_num = min(t_list)
index = c_list.index(min_num)
c_list[i], c_list[index] = c_list[index], c_list[i]
return c_list
if __name__ == '__main__':
c_list = [3,5,4,1,2]
ret_list = selection_sort(c_list)
print(ret_list)
冒泡排序:
def bubble_sort(c_list):
length = len(c_list)
for i in range(length-1):
for j in range(length-1-i):
if c_list[j] > c_list[j+1]:
c_list[j], c_list[j+1] = c_list[j+1], c_list[j]
return c_list
if __name__ == '__main__':
c_list = [3,5,4,1,2]
ret_list = bubble_sort(c_list)
print(ret_list)
蛮力查找
def sequential_search(c_list, t):
for item in c_list:
if item == t:
return 'found'
return 'not found'
if __name__ == '__main__':
c_list = [3,4,5,1,2]
t = 3
print(sequential_search(c_list, t))
t = 6
print(sequential_search(c_list, t))
书上还有一个蛮力字符串匹配,蛮力法实在是简单暴力,这个就略了。
下面还是在蛮力法,不过是对一些著名问题的蛮力求解的解法,如凸包、背包、旅行商等等。以后章节会有其相应的最优解法。
最近对问题
要求:找出一个包含n个点的集合中距离最近的两个点。
import math
def closest_points(p_list):
length = len(p_list)
dmin = float('inf')
dmin_node1 = dmin_node2 = 0
for i in range(length-1):
p1 = p_list[i]
for j in range(i+1, length):
p2 = p_list[j]
dis = math.sqrt(pow(p1[0]-p2[0],2)+pow(p1[1]-p2[1],2))
if dis < dmin:
dmin = dis
dmin_node1 = p1
dmin_node2 = p2
print('closest points is:',p1,p2)
print('min distance is:',dmin)
if __name__ == '__main__':
p_list = [(1,1), (2,2), (2,1)]
closest_points(p_list)
也可以减少计算,不计算平方根函数,只求平方和。
凸包问题
凸集合:在欧氏空间中,凸集是对于集合内的每一对点,连接该对点的直线段上的每个点也在该集合内。
凸包:对于平面上n个点的集合,它的凸包就是包含所有这些点(或者在内部,或者在边界上)的最小凸多边形。对这个概念,其实还蛮抽象的,书上有一个更加温和的解释,把所讨论的点想象成定在胶合板上的钉子,胶合板代表平面,撑开一根橡皮筋,把所有的钉子都围住,然后松开手,凸包就是以橡皮圈为边界的区域。
因此,凸包问题就是为一个n个点的集合构造凸包的问题。
用蛮力法可以这样理解,线段构成了凸包的边界,那么就可以基于这个设计一个简单但缺乏效率的算法:对于一个n个点集合中的两个点Pi和Pj,当且仅当该集合中的其他点都位于这两点的直线的同一边时,他们的连线是该集合凸包边界的一部分。对每一对点都做一遍检验后,满足该条件的线段就构成了该凸包的边界。
def convex(n_list):
length = len(n_list)
for i in range(length-1):
pi = n_list[i]
for j in range(i+1, length):
pj = n_list[j]
a = pj[1] - pi[1]
b = pi[0] - pj[0]
c = pi[0]*pj[1] - pi[1]*pj[0]
j_dic = {}
for k in range(length):
pk = n_list[k]
if k!=i and k!=j:
if a*pk[0]+b*pk[1] < c:
j_dic['negative'] = True
else:
j_dic['positive'] = True
if len(j_dic) == 1:
print('edge:',pi,pj)
if __name__ == '__main__':
n_list = [(0,0),(1,0),(0.5,1)]
n_list = [(5,0),(4,2),(0,0),(3,1),(6,1),(4,3),(0,3),(2,2)]
convex(n_list)
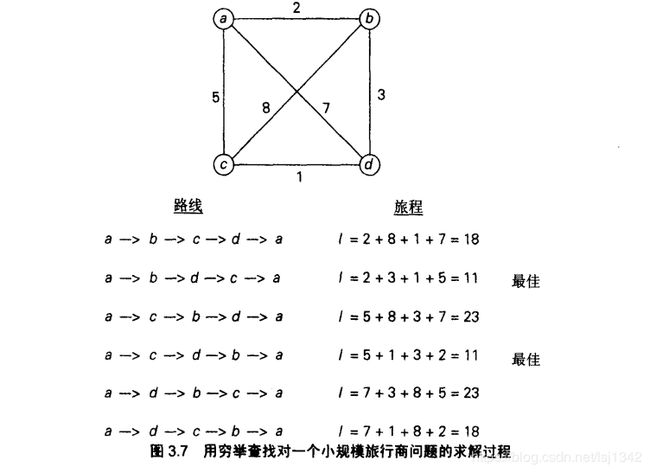
旅行商问题
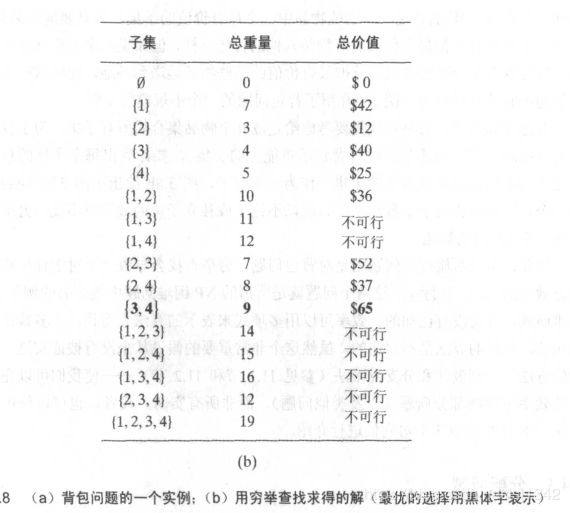
背包问题

分配问题

总结
蛮力法的优点就是能够以一种简单的方法解决问题,暴力求解,直接基于问题的描述和概念定义等切入。
缺点就是蛮力法基本上效率都不高,但是也可以在其基础上进行适当的修改提升效率。