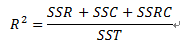《统计学》学习笔记之方差分析

鄙人学习笔记

---

---

方差分析

从形式上看，方差分析是比较多个总体的均值是否相等，但本质上它所研究的是变量之间的关系。在研究一个(或多个)分类型自变量与一个数值型因变量之间的关系时，方差分析就是其中的主要方法之一。

方差分析引论

• 方差分析

表面上看，方差分析是检验多个总体均值是否相等的统计方法，但本质上它所研究的是分类型自变量对数值型因变量的影响。例如，变量之间有没有关系，关系的强度如何等。
方差分析就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。

• 方差分析与假设检验的比较

①假设检验进行两两比较繁琐。例如，设4个总体的均值分别为μ₁,μ₂,μ₃,μ₄，如果用一般假设检验方法，如t检验，一次只能研究两个样本，要检验4个总体的均值是否相等，需要作6次检验。

②一般来说，随着增加个体显著性检验的次数，偶然因素导致差别的可能性也会增加(并非均值真的存在差别)。

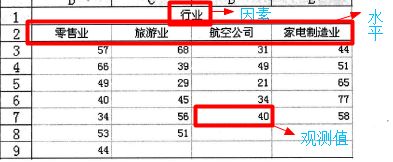
• 因素、水平和观测值

在方差分析中，所要检验的对象称为因素或因子。因素的不同表现称为水平或处理。每个因子水平下得到的样本数据称为观测值。

方差分析的基本思想

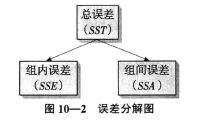
• 误差分解

在方差分析中，数据的误差是用平方和来表示，总平方和可分解为组内平方和与组间平方和。

总平方和：记为SST。它反映了全部观测值的离散状况。
组内平方和：也称为误差平方和或残差平方和，记为SSE。它反映了每个样本内各观测值的离散状况。组内误差只含有随机误差。
组间平方和：也称为因素平方和，记为SSA。它反映了样本均值之间的差异程度。组间误差包含随机误差和系统误差。

误差分解图：

• 误差分析

如果在组间误差中只包含随机误差，而没有系统误差。这时，组间误差与组内误差经过平均后的数值(称为均方或方差)，就应该很接近，它们的比值就会接近1。相反，如果在组间误差中不仅包含随机误差，而且包含系统误差。这时组间误差平均后的数值就会大于组内误差平均后的数值，它们之间的比值就会大于1。当这个比值大到某种程度时，就认为因素的不同水平之间存在着显著差异，也就是自变量对因变量有显著影响。

方差分析基本假定

①每个总体都应服从正态分布。也就是说，对于因素的每一个水平，其观测值是来自正态分布总体的简单随机样本。
②各个总体的方差必须相同。也就是说，各组观察数据是从具有相同方差的正态总体中抽取的。
③观测值是独立的。

在上述假定成立的前提下，要分析自变量对因变量是否有影响，形式上也就转化为检验自变量的各个水平(总体)的均值是否相等。

问题的一般提法

设因素有k个水平，每个水平的均值分别用μ₁，μ₂，…，μ_k表示，要检验k个水平(总体)的均值是否相等，需要提出如下假设:

单因素方差分析

根据所分析的分类型自变量的多少，方差分析可分为单因素方差分析和双因素方差分析。当方差分析中只涉及一个分类型自变量时称为单因素方差分析。

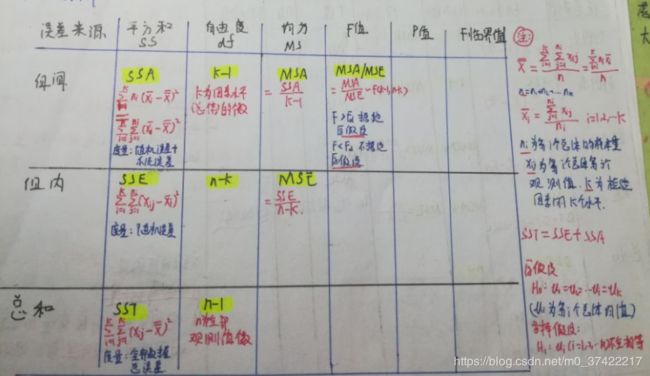
分析步骤

• 数据结构

• 分析步骤

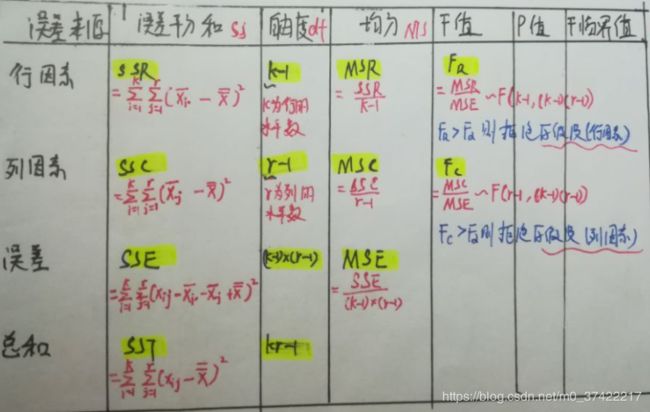
• 表格结构

关系强度测量

实际上，只要组间平方和不等于零.就表明两个变量之间有关系(只是是否显著的问题)。

如何度量两个变量之间的关系呢？可以用组间平方和(SSA)占总平方和(SST)的比例大小来反映，这一比例记为R²:

其平方根R就可以用来测量两个变量之间的关系强度。

方差分析中的多重比较

要判断到底哪些均值之间存在差异，可以使用多重比较的方法。

多重比较方法有许多种，这里介绍由费希尔提出的最小显著差异方法，缩写为LSD。
使用该方法进行检验的具体步骤为：

双因素方差分析

当方差分析中涉及两个分类型自变量时，称为双因素方差分析。

在双因素方差分析中，有两个影响因素。
若两个因素对因变量影响是相互独立的，这时的双因素方差分析称为无交互作用的双因素方差分析。
若两个因素的搭配还会对因变量产生一种新的影响，这时的双因素方差分析称为有交互作用的双因素方差分析，或称为可重复双因素分析。

无交互作用的双因素方差分析

分析步骤(与单因素方差分析步骤类似)

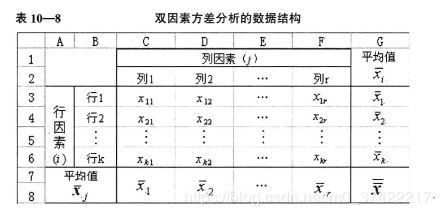
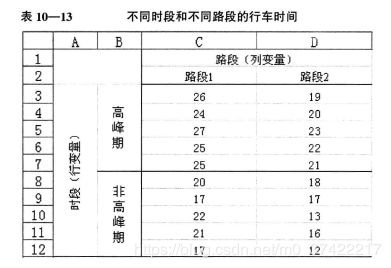
• 数据结构

• 表格结构

关系强度测量

两个变量合起来与因变量之间的关系强度究竟如何呢?首先我们看一下联合效应这个概念。
两个自变量对因变量的联合效应为行平方和与列平方和的加总。
联合效应与总平方和的比值定义为R²,即：

其平方根R则反映了这两个自变量合起来与因变量之间的关系强度.

有交互作用的双因素方差分析

分析步骤(与单因素方差分析步骤类似)

• 数据结构

• 表格结构
  

关系强度测量

R²：

其平方根R则反映了这两个自变量合起来与因变量之间的关系强度.