吴恩达机器学习课后作业深度解析（附答案）（ex2）

作业ex2题目及答案源码下载地址ex2题目及答案

一、逻辑回归

问题背景，根据学生两门课的成绩和是否入学的数据，预测学生能否顺利入学

1. plotData.m：数据可视化

% Find Indices of Positive and Negative Examples
pos = find(y == 1); neg = find(y == 0);
% Plot Examples
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, 'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y','MarkerSize', 7);

matlab中find函数返回索引列表，详见Matlab 之 find()函数

2. sigmoid.m：完成sigmoid函数
   $$g(z)=\frac{1}{1+e^{-z}}$$

g = 1 ./ ( 1 + exp(-z) ) ;

hypothesis函数定义为
$$h_{\theta }(x)=g({\theta }^{T}x)$$

3. costFunction.m：计算代价和梯度
   逻辑回归似然函数取对数为（详见视频课程）
   $$l(\theta )=\sum _{i=1}^m[y^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$
   要想取得最大似然估计，可令代价函数为
   $$J(\theta )=-\frac{1}{m}l(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}log{h}_{\theta }(x^{(i)})-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$
   求导得
   $$\frac{\partial }{\partial {\theta }_j}J(\theta )=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

J= -1 * sum( y .* log( sigmoid(X*theta) ) 
    + (1 - y ) .* log( (1 - sigmoid(X*theta)) ) ) / m ;
grad = ( X' * (sigmoid(X*theta) - y ) )/ m ;

4. 利用fminunc函数求得最小代价

options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, cost] = fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

其中，GradObj:On 表示使用自己的梯度公式，Maxlter:400表示最大迭代次数。costFunction函数完整形式为function [J, grad] = costFunction(theta, X, y)。
该函数作用是求函数的最小值，代价函数虽然复杂，但是xy等数据是已知的，未知的只有$\theta$的分量，这就相当于几元一次函数的求最值问题。

5. plotDecisionBoundary.m：画决策边界

这里只考虑本题的输入$(1,x_2,x_3)$，sigmoid函数的分界点是$z=0$，即
$${\theta }^{T}x={\theta }_1+{\theta }_2{x}_2+{\theta }_3{x}_3=0$$
要画一条直线将平面分开，首先求得$x_2$的最小值和最大值，然后根据上式求得相应的$x_3$，两点确定一条直线。

 plot_x = [min(X(:,2))-2,  max(X(:,2))+2];
 plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));
 plot(plot_x, plot_y)

7. predict.m：计算模型精确度
   根据给定的数据，查看预测值与实际值是否吻合，先计算预测值

k = find(sigmoid( X * theta) >= 0.5 );
p(k)= 1;

与实际值比较，相加除以总数（均值）

mean(double(p == y)) * 100)

二、逻辑回归（多项式回归）

问题背景：根据以往微晶片两项测试和是否合格的数据，进行预测。

1. plotData.m：数据可视化

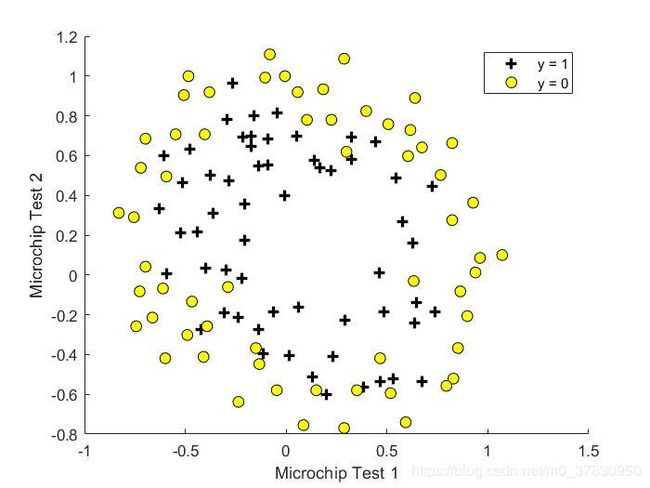
2. mapFeature.m: 特征提取
   从图中数据分布可以看到，显然不再是线性边界。那么便需要将每个点的特征进一步提取出来。
   $$\left[\begin{array}{r}{x}_1\\ x_2\end{array}\right]<=>\left[\begin{array}{r}1\\ x_1\\ x_2\\ x_1^2\\ x_1{x}_2\\ x_2^2\\ .\\ .\\ .\\ x_1^5{x}_2\\ x_2^6\end{array}\right]$$
   从二维变换到28维。

degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end

3. costFunctionReg.m：计算代价和梯度
   为了防止过拟合，采用L2正则化方法，代价函数为
   $$J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}log{h}_{\theta }(x^{(i)})-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{m}\sum _{j=2}^n{\theta }_j^2$$
   注意：第一项${\theta }_1$不参与正则化
   梯度为
   $$\begin{array}{rl}\frac{\partial }{\partial {\theta }_1}J(\theta )& =\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_1^{(i)}forj=1\\ \frac{\partial }{\partial {\theta }_j}J(\theta )& =\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_{j}forj\ge 2\end{array}$$

theta_1=[0;theta(2:end)];    % 先把theta(1)拿掉，不参与正则化
J= -1 * sum( y .* log( sigmoid(X*theta) ) + (1 - y ) 
	.* log( (1 - sigmoid(X*theta)) ) ) / m  + lambda/(2*m) * theta_1' * theta_1; 
grad = ( X' * (sigmoid(X*theta) - y ) )/ m + lambda/m * theta_1; 

4. 利用fminunc函数求解
5. plotDecisionBoundary.m：画决策边界

  u = linspace(-1, 1.5, 50);
  v = linspace(-1, 1.5, 50);
  z = zeros(length(u), length(v));
  for i = 1:length(u)
      for j = 1:length(v)
          z(i,j) = mapFeature(u(i), v(j))*theta;
      end
  end
  z = z'; % important to transpose z before calling contour
  contour(u, v, z, [0, 0], 'LineWidth', 2)

这里利用contour函数，[0,0]表示画值为0的等高线，[0,1,2]则表示画值为0,1,2的三条等高线。