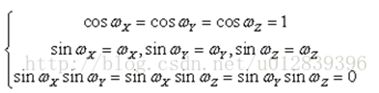地理空间坐标系统-不同椭球基准间的坐标转换

基于同一个椭球基准，可以构建三类地理空间坐标系：大地球面坐标系、大地空间直角坐标系、大地投影坐标系。由于坐标原点和椭球长短半径等都相同，这三类坐标系之间可以通过无损的数学方法相互之间进行转换。那么现在问题来了，不同椭球基准（在全球范围来看存在成百上千的椭球基准）之间的坐标怎么转换？比如，北京54、西安80、国家2000，特别是在我国，现在主推国家2000坐标系，那么如何将历史的测绘成果（北京54和国家2000）都转到国家2000坐标系下？就是本篇讨论的主题。

先对【七参数坐标转换】，做个简单介绍：

两个不同的三维空间直角坐标系之间转换时，通常使用七参数模型（数学方程组）。在该模型中有七个未知参数，即：
　　（1）三个坐标平移量（△X，△Y，△Z），即两个空间坐标系的坐标原点之间坐标差值；
　　（2）三个坐标轴的旋转角度（△α，△β，△γ），通过按顺序旋转三个坐标轴指定角度，可以使两个空间直角坐标系的XYZ轴重合在一起。
　　（3）尺度因子K，即两个空间坐标系内的同一段直线的长度比值，实现尺度的比例转换。通常K值几乎等于1。 以上七个参数通常称为七参数。运用七参数进行的坐标转换称为七参数坐标转换。

如何简单理解七参数坐标转换了？建议这么去想，把此刻手机或电脑前的你放在一个三维空间直角坐标中，要准确描述你当前的位置只使用（X,Y,Z）是不够的。例如：上一秒你还在和面前的同事聊工作，下一秒你身边一美女经过，你转身去看。思考此间的变化，上一秒和下一秒你其实在原地没有发生移动，但在三维空间中你确实发生了变化了（你转身了）。因此在三维空间中要准确描述一个事物的位置，除了三个平移值外，还需要俯角、仰角、旋转角，有了这6个值，不管你在原地转圈、倒立，还是翻滚在三维空间坐标系中都可以准确表示。两个三维空间直角坐标系之间的转换就是这两个坐标系中六个分量的映射关系的建立，外加一个压缩映射关系。

本编以WGS84大地基准下的坐标到国家2000大地基准下的坐标转换为例。两个基准之间的转换采用七参数坐标转换。

先看下图：

 

 

在同一个大地基准下面，空间直角坐标系和大地球面坐标系是唯一的，地球椭球到平面存在多种空间投影方式，此处选用【高斯投影平面坐标系】。

从上述流程图中，我们不难看出，在两个不同椭球基准之间进行坐标转换时，不管拿到的坐标是平面坐标，还是空间直角坐标，原坐标都必须先转换成所在椭球基准对应的空间直角坐标，再通过【七参数坐标转换】转换成目标坐标所在椭球基准对应的空间直角坐标，然后在同一个椭球基准内进行坐标转换，最终得到想要的目标坐标。

举例说明：先有WGS84的经纬度坐标，现在想要GCC2000坐标系下对应的高斯投影坐标。那么它的转换流程如下：

WGS84大地球面坐标（经度、纬度）→【球面坐标到空间直角坐标正转】→WGS84空间直角坐标（X,Y,Z）→【七参数坐标转换】→CGC2000空间直角坐标（X,Y,Z）→【球面坐标到空间直角坐标反转】→ CGC2000大地球面坐标（经度、纬度） →【高斯正向投影】  →  CGC2000高斯平面坐标。

具体的实现过程-已经获得两个空间直角坐标之间转换的七参数△X，△Y，△Z，ωx，ωy，ωz，m情况

同一个椭球基准内的坐标转换，在前面一章中已经给出了相关的逻辑和对应的C#代码。此处重点说一下，七参数坐标转换的实现(泊尔沙模型)。 假设已经知道两个坐标

此模型中的坐标转换关系为：旋转→缩放→平移。此公式中△X，△Y，△Z是坐标变换平移参数，ωx,ωy,ωz分别为绕三个旋转的坐标轴旋转角度参数，（1+m）是比例因子。此公式，根据期望的转换精度通过矩阵变换可以进一步进行优化。

以网上的一个简化方式为例：

令：

那么转换公式就变为：

令：

那么转换公式最终就简化为：

此公式可以简写为：B=AX

假如已经知道两个空间直角坐标之间转换的七个参数：△X，△Y，△Z，ωx，ωy，ωz，m

将ωx,ωy,ωz,m四个参数代入求得：a1,a2,a3,a4，再把已经知道的△X，△Y，△Z代入构建转换X矩阵，将已知的源空间直角坐标代入构建A举证，既求得B矩阵，B矩阵的三个项对应所求空间直角坐标的X2,Y2,Z2。

具体的实现过程-事先无法获取两个空间直角坐标转换七参数的情况

通过精确测量测区内三个以上的控制点坐标对，进行七参数的反算。回看上述简化后的转换公式B=AX。不难看出此公式符合最小二乘的形式。依照最小二乘求解法：反算B=AX公式中的X，此时

X矩阵中：△X，△Y，△Z保留，ωx，ωy，ωz，m通过下面的简单计算获得。

 

下一篇，分享一下此处用到的两个公式的代码实现，C#代码。