关键词:粒子群算法、python
一、粒子群算法概述
粒子群算法,也称粒子群优化算法或鸟群觅食算法(Particle Swarm Optimization),缩写为 PSO,属于进化算法的一种,和模拟退火算法相似,它也是从随机解出发,通过迭代寻找最优解,它也是通过适应度来评价解的品质,但它比遗传算法规则更为简单,它没有遗传算法的“交叉”(Crossover) 和“变异”(Mutation) 操作,它通过追随当前搜索到的最优值来寻找全局最优。这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视,并且在解决实际问题中展示了其优越性。
原理讲解可参考:粒子群算法入门及实践、粒子群算法详解,这些例子都有原理,还有java、matlab实现,本例是用Python及相关第三方包实现粒子群算法
二、例题
我用上面那个博客的例题:查找这个函数的最优解
三、粒子群的Python实现
1.首先是引入包
import numpy as np
import pandas as pd
from collections import Iterable, Counter
2.打好框架
首先我们要明确粒子群算法的步骤,下面是流程图:我们所要做的步骤,分别是初始化(init)、循环更新位置、速度(Update_position)与最大值记录(Update_best),以及输出结果(info),并且将迭代部分的两步包在一起,形成一个函数(pso)
class PSO:
def __init__(self, func, bound, POP_SIZE, w=1, c1=0.2, c2=0.2, v_max=0.05, *, var_name=None):
pass
def get_fitness(self):
pass
def update_position(self):
pass
def update_best(self):
pass
def pso(self):
pass
def info(self):
pass
3.__init__分析和实现
前面已经反复提到过,__init__方法会作为初始化的函数,需要传递方法、参数,这在我们上面定义的函数签名上有很好的体现。
首先是func参数,按理来说,这里应该是函数(method),不过这是我的习惯,喜欢写方法(function),无伤大雅;这里用来传递函数引用,无论是def出来的函数,还是lambda表达式出来的函数都没问题。
bound参数为边界,就是变量的取值范围,数据格式为((x_min, x_max), (y_min, y_max), z,...),简单来说就是个容器,里面装着许多个二元容器或单个变量。例如:[(0, 60), (20, 70), (23, 45.5), 7],其中二元容器代表变量的上下限,单个变量为变量只能取得唯一值。此处只支持这些,如果有类似:(min, None)这种单边界或((min1, max1), (min2, max2))这种多边界的需求,可以自己去实现。
POP_SIZE为粒子数,可以看成一个范围内觅食鸟的个数。
w、c1、c2是后面更新公式所需要的参数,我们更新的时候再讲解。
v_max为初始速度的最大值。
var_name是变量名,None为默认,前面加上*参数的意思是:想要给var_name赋值,必须用var_name=...的形式。
参数讲解完毕,先上__init__代码:
def __init__(self, func, bound, POP_SIZE, w=1, c1=0.2, c2=0.2, v_max=0.05, *, var_name=None):
bounds = Counter([isinstance(a, Iterable) for a in bound])[True]
Var_size = int(np.ceil(POP_SIZE ** (1/bounds)))
vals = [np.linspace(var[0], var[1], Var_size) if isinstance(var, Iterable) else np.array([var]) for var in bound]
vals = np.array(list(map(lambda var: var.flatten(), np.meshgrid(*vals))))
self.var_quantity, self.POP_SIZE = vals.shape
self.func = func
self.bound = bound
self.w = w
self.c1=c1
self.c2=c2
self.v_max = v_max
self.var_name = var_name
# 粒子
self.particles = np.array(list(zip(*vals)))
self.velocity = np.random.rand(*self.particles.shape) * v_max
# 粒子最优位置
self.person_best = self.particles.copy()
# 全局最优位置
self.global_best = max(self.person_best, key=lambda particle: self.func(*particle)).copy()
让我们先看看前五行是什么意思。
第一行,用计数器数一个推导列表,这个列表由bool类型组成,当前元素含义是:bound参数当前位置元素是否可迭代(既是二元组),然后查里面有多少个True;因此第一行的含义是:看变量中有多少个变量是在范围内取值。
第二行实现的是这个公式:,什么含义呢?想想,假如我们有、两个变量,各取10个数字,那么的元组是否就有100种可能的取值?以此推广,假如有三个变量,各取5个值,元组就有125种可能取值;假如我们需要100个粒子,有三个变量,那么就,结果是5,虽然能得到的是125个粒子,但结果近似;这里的算法不但是根据变量数,还要求变量不能是那种唯一取值的变量,因此开根号数由第一行得到。
第三行,确定所有变量的取值;如果是范围内取值,将会由其最小值到最大值,个数为上一行计算的进行填充;如果是单个值,就只计入一个值。例如上面的例题,、变量为范围取值,是单个取值,我们需要100个粒子,上面计算的,根据和的取值范围,和的取值列表都为[0, 6.667, 13.333, 20, 26.667, 33.333, 40, 46,667, 53,555, 60],而的取值列表为[30]。这样能做到像网状一样的均匀取值。
第四行,np.meshgrid函数就能做到找出所有的取值,我们将所有变量传入,它将返回“变量数+1”维的数组,最外面一层可以解包给各个变量,每个变量持有“变量数”维数组,我们可以将其看做“变量数-1”维数组,每一个维度为其他变量的取值个数,最内层的元素是原来的变量本身。听起来很绕口,自己试试就明白了,这个方法常用于多维作图铺开取值网格。不过多维的数组处理起来很头疼,因此我将它们都用fatten铺成了一维数组,原来位置的对应关系没有改变,现在vals成了二维数组,一维数的含义是变量数,二维数含义是最终粒子个数。这就是第五行做的事。
后面一堆参数赋值没什么好说的。
然后是粒子注释的下一行,vals变量的操作还是有些恶心,不符合我的处理思维,因此我将其转置(我常用的转置操作,不过vals是numpy.array类型,所以用self.particles=vals.T就能实现),这样就会变成一个容器,内部的每一个元素都是位置的集合。
velocity是和粒子同样维度的随机序列,意思是每一个粒子的每一个变量都有速度。
最后记录当前位置为粒子最优位置。
4.get_fitness
就是获得所有粒子的适应度,因此将粒子容器中的每一个粒子代入到函数func中计算即可。
def get_fitness(self):
return np.array([self.func(*particle) for particle in self.particles])
之前我写函数直接return func(*self.particles),这样能调用numpy中数组的矩阵运算,但这个函数中存在判断,因此不能简单送入方法,而选择用列表推导实现。
5.update_position
更新位置和速度的函数,让我们先看数学的式子:其中:
这里,是__init__中随机的,是__init__中均匀铺开的粒子,、、是需要我们试验填入的参数,自身最优和全局全时刻最优在__init__中已被初始化,并在后续会有更新。
怎么理解上面的公式呢?
首先是速度,当前速度与四个因素有关:之前的速度、之前的位置、全局最优位置、自身最优位置。
自身速度会有一定程度保留下来,惯性因子就决定了保留速度的程度。
后面两个式子,我们想,假如觅食中的鸟知道种群在哪里找到的食物最多,也记住了自己在哪里找到了最多的食物,假如当前位置不尽如人意,就会向这两个地方赶,而离的越远,就要越快地赶去,因此位置两者之差越大,对速度加成越高。加成的程度、则是要我们多次试验,、提供了随机度。
可以看下面的图:
红底为鸟群得到的食物分布情况,当前的黑色粒子正以浅绿色的方向运动,下一时刻它的运行轨迹,同时被三个力拉扯:原有的行动方向,自身记录最高点,全局记录最高点。是不是有点像我们之前学的受力分解?
根据公式,我们写出更新位置和速度的代码
def update_position(self):
for index, particle in enumerate(self.particles):
V_k_plus_1 = self.w * self.velocity[index] \
+ self.c1*np.random.rand()*(self.person_best[index]-particle) \
+ self.c2*np.random.rand()*(self.global_best-particle)
self.particles[index] = self.particles[index] + V_k_plus_1
self.velocity[index] = V_k_plus_1
for i, var in enumerate(particle):
if isinstance(self.bound[i], Iterable):
if var < self.bound[i][0]:
self.particles[index][i] = self.bound[i][0]
elif var > self.bound[i][1]:
self.particles[index][i] = self.bound[i][1]
elif var != self.bound[i]:
self.particles[index][i] = self.bound[i]
上面一段先算出的速度,然后改变位置和原有速度;下面一段是用于检查,毕竟变量是有取值范围的,如果超出范围,将重置为边界,如果是唯一取值,将让值不变。
6.update_best
没什么好说的,就是更新最优记录
def update_best(self):
global_best_fitness = self.func(*self.global_best)
person_best_value = np.array([self.func(*particle) for particle in self.person_best])
for index, particle in enumerate(self.particles):
current_particle_fitness = self.func(*particle)
if current_particle_fitness > person_best_value[index]:
person_best_value[index] = current_particle_fitness
self.person_best[index] = particle
if current_particle_fitness > global_best_fitness:
global_best_fitness = current_particle_fitness
self.global_best = particle
7.pso
执行两个更新
def pso(self):
self.update_position()
self.update_best()
8.info
输出当前粒子信息,如果没传入变量名(var_name为None),就默认采用这种形式。
def info(self):
result = pd.DataFrame(self.particles)
if self.var_name == None:
result.columns = [f'x{i}' for i in range(len(self.bound))]
else:
result.columns = self.var_name
result['fitness'] = self.get_fitness()
return result
四、实验
我们准备好需要传递的参数,传入构造方法里面
func = lambda x, y, m: 30*x-y if x < m and y < m else 30*y-x if x=m else x**2-y/2 if x>=m and y 然后不断迭代,由于粒子群算法属于群体进化,因此我们可以打印总体的加和方式,体现进化的效果,并打印出全体最优解及最优取值:
for _ in range(1000):
pso.pso()
print(pso.get_fitness().sum())
print(pso.global_best, func(*pso.global_best))
输出结果上面还有,省略不放了。
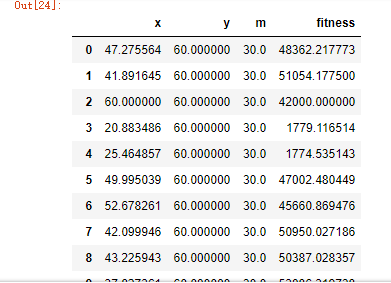
此时我们调用info即可看到格式化的结果输出:
pso.info()
可以看出,总体进化不是很理想,但有不少个体已经接近全局最优,不断调试参数,或许能改善这种情况。
五、总结
和遗传算法一样,粒子群算法是对现实中规律的总结和应用,具体怎么使用,要看我们如何抽象问题;此例是解决一个普通的数学优化问题,但假如我们对其他问题抽象,只要能通过一系列参数得到一个值,就可抽象为适应度函数;只要能体现过去状态、最优记录,就能抽象为为pso算法。
如果我们遇到其他问题,即使和当前问题不是很像,但动脑抽象,大致贴和相关算法,说不定就能得到意外的解决方案。