VINS_FUSION入门系列－优化optimization

代码最核心的地方就是优化和滑动窗口,代码主要和VINS_MONO分成的三部分差不多,视觉由于使用的双目有所改变.优化主要就是计算残差,雅克比矩阵和信息矩阵.
VINS_MONO
VINS_FUSION
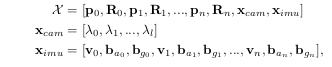
从上图可以看出,总体VINS_MONO和VINS_FUSION求解的变量差不多.下面具体分析VINS_FUSION的优化.

1.1 视觉约束

for (auto &it_per_frame : it_per_id.feature_per_frame)
        {
            imu_j++;
            if (imu_i != imu_j)//既,本次不是第一次观测到
            {
                Vector3d pts_j = it_per_frame.point;
                ProjectionTwoFrameOneCamFactor *f_td = new ProjectionTwoFrameOneCamFactor(pts_i, pts_j, it_per_id.feature_per_frame[0].velocity, it_per_frame.velocity,
                    it_per_id.feature_per_frame[0].cur_td, it_per_frame.cur_td);
                problem.AddResidualBlock(f_td, loss_function, para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Feature[feature_index], para_Td[0]);
                    /* 相关介绍:
                    1 只在视觉量测中用了核函数loss_function 用的是huber
                    2 参数包含了para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Feature[feature_index], para_Td[0] */
            }

            // 如果是双目的
            if(STEREO && it_per_frame.is_stereo)
            {                
                Vector3d pts_j_right = it_per_frame.pointRight;
                if(imu_i != imu_j) //既,本次不是第一次观测到
                {
                    ProjectionTwoFrameTwoCamFactor *f = new ProjectionTwoFrameTwoCamFactor(pts_i, pts_j_right, it_per_id.feature_per_frame[0].velocity, it_per_frame.velocityRight,
                        it_per_id.feature_per_frame[0].cur_td, it_per_frame.cur_td);
                    problem.AddResidualBlock(f, loss_function, para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Ex_Pose[1], para_Feature[feature_index], para_Td[0]);
                }
                else//既,本次是第一次观测到
                {
                    ProjectionOneFrameTwoCamFactor *f = new ProjectionOneFrameTwoCamFactor(pts_i, pts_j_right, it_per_id.feature_per_frame[0].velocity, it_per_frame.velocityRight,
                        it_per_id.feature_per_frame[0].cur_td, it_per_frame.cur_td);
                    problem.AddResidualBlock(f, loss_function, para_Ex_Pose[0], para_Ex_Pose[1], para_Feature[feature_index], para_Td[0]);
                }
               
            }
            f_m_cnt++;
        }
    }

如上上面的代码,当系统刚开始启动的时候先运行

1.1 ProjectionOneFrameTwoCamFactor()

此函数可以理解成将左目的特征点投影到右目进行计算.下图为需要求解的量

残差代码

 Eigen::Vector3d pts_i_td, pts_j_td;
    pts_i_td = pts_i - (td - td_i) * velocity_i;
    pts_j_td = pts_j - (td - td_j) * velocity_j;

    Eigen::Vector3d pts_camera_i = pts_i_td / inv_dep_i;
    Eigen::Vector3d pts_imu_i = qic * pts_camera_i + tic;
    Eigen::Vector3d pts_imu_j = pts_imu_i;
    Eigen::Vector3d pts_camera_j = qic2.inverse() * (pts_imu_j - tic2);
    Eigen::Map residual(residuals);

#ifdef UNIT_SPHERE_ERROR 
    residual =  tangent_base * (pts_camera_j.normalized() - pts_j_td.normalized());
#else
    double dep_j = pts_camera_j.z();
    residual = (pts_camera_j / dep_j).head<2>() - pts_j_td.head<2>();
#endif

    residual = sqrt_info * residual;

雅克比矩阵对于不易求导的就是个给一个微小的扰动进行求解的,对于td这个可以求导的就直接求导就好.雅克比的代码比较长就不贴了,可以去git一下源码就可以看得到.
信息矩阵代码

1.2 ProjectionTwoFrameOneCamFactor

相对与上面的函数,少求解了一个相机到IMU的外参,多求解i,j时刻的位姿.

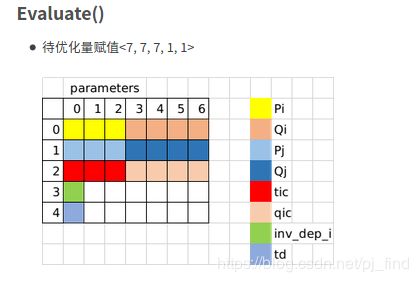
残差代码

    Eigen::Vector3d pts_i_td, pts_j_td;
    pts_i_td = pts_i - (td - td_i) * velocity_i;
    pts_j_td = pts_j - (td - td_j) * velocity_j;
    Eigen::Vector3d pts_camera_i = pts_i_td / inv_dep_i;
    Eigen::Vector3d pts_imu_i = qic * pts_camera_i + tic;
    Eigen::Vector3d pts_w = Qi * pts_imu_i + Pi;
    Eigen::Vector3d pts_imu_j = Qj.inverse() * (pts_w - Pj);
    Eigen::Vector3d pts_camera_j = qic.inverse() * (pts_imu_j - tic);
    Eigen::Map residual(residuals);

#ifdef UNIT_SPHERE_ERROR 
    residual =  tangent_base * (pts_camera_j.normalized() - pts_j_td.normalized());
#else
    double dep_j = pts_camera_j.z();
    residual = (pts_camera_j / dep_j).head<2>() - pts_j_td.head<2>();
#endif

    residual = sqrt_info * residual;

上述代码就是将第i帧的特征点投影到第j帧中求解重投影误差的.

1.3 ProjectionTwoFrameTwoCamFactor

相对于上述的函数,多求解了相机与IMU之间的外参.
残差代码

 Eigen::Vector3d pts_i_td, pts_j_td;
    pts_i_td = pts_i - (td - td_i) * velocity_i;
    pts_j_td = pts_j - (td - td_j) * velocity_j;

    Eigen::Vector3d pts_camera_i = pts_i_td / inv_dep_i;
    Eigen::Vector3d pts_imu_i = qic * pts_camera_i + tic;
    Eigen::Vector3d pts_w = Qi * pts_imu_i + Pi;
    Eigen::Vector3d pts_imu_j = Qj.inverse() * (pts_w - Pj);
    Eigen::Vector3d pts_camera_j = qic2.inverse() * (pts_imu_j - tic2);
    Eigen::Map residual(residuals);

#ifdef UNIT_SPHERE_ERROR 
    residual =  tangent_base * (pts_camera_j.normalized() - pts_j_td.normalized());
#else
    double dep_j = pts_camera_j.z();
    residual = (pts_camera_j / dep_j).head<2>() - pts_j_td.head<2>();
#endif

    residual = sqrt_info * residual;

以上就将视觉部分约束整理一下,下面对IMU预积分约束进行整理.

2.IMU约束

IMU约束与VINS_MONO是差不多的.

2.1 IMU预积分

上面的公式用的一个大佬的整理VINS_MONO的笔记截图出来的.

2.2 约束

残差代码

    // 计算残差
    Eigen::Matrix evaluate(const Eigen::Vector3d &Pi, const Eigen::Quaterniond &Qi, const Eigen::Vector3d &Vi, const Eigen::Vector3d &Bai, const Eigen::Vector3d &Bgi,
                                          const Eigen::Vector3d &Pj, const Eigen::Quaterniond &Qj, const Eigen::Vector3d &Vj, const Eigen::Vector3d &Baj, const Eigen::Vector3d &Bgj)
    {
        Eigen::Matrix residuals;

        Eigen::Matrix3d dp_dba = jacobian.block<3, 3>(O_P, O_BA);
        Eigen::Matrix3d dp_dbg = jacobian.block<3, 3>(O_P, O_BG);

        Eigen::Matrix3d dq_dbg = jacobian.block<3, 3>(O_R, O_BG);

        Eigen::Matrix3d dv_dba = jacobian.block<3, 3>(O_V, O_BA);
        Eigen::Matrix3d dv_dbg = jacobian.block<3, 3>(O_V, O_BG);

        Eigen::Vector3d dba = Bai - linearized_ba;
        Eigen::Vector3d dbg = Bgi - linearized_bg;

        Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg);
        Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg;
        Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg;

        residuals.block<3, 1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt) - corrected_delta_p;
        residuals.block<3, 1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
        residuals.block<3, 1>(O_V, 0) = Qi.inverse() * (G * sum_dt + Vj - Vi) - corrected_delta_v;
        residuals.block<3, 1>(O_BA, 0) = Baj - Bai;
        residuals.block<3, 1>(O_BG, 0) = Bgj - Bgi;
        return residuals;
    }

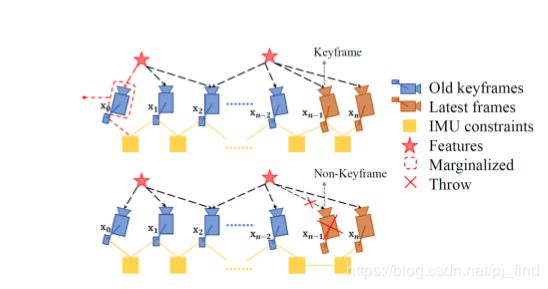
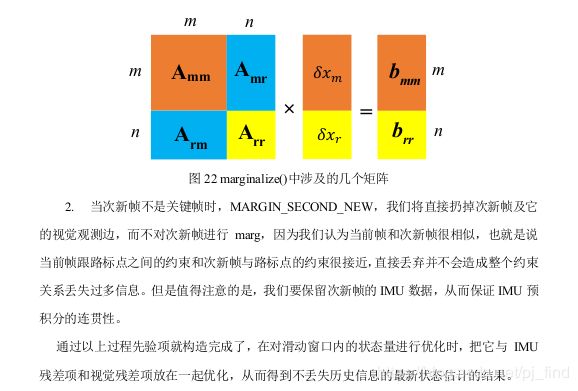
3. 边缘化的先验信息

VINS采用了两种边缘化的策略

    // -----------函数会通过shur补操作进行边缘化，然后再从边缘化后的信息矩阵中恢复出来雅克比矩阵 linearized_jacobians 和残差 linearized_residuals ，
    //------------这两者会作为先验残差带入到下一轮的先验残差的雅克比和残差的计算当中去。
    //舒尔补
    Eigen::VectorXd bmm = b.segment(0, m);
    Eigen::MatrixXd Amr = A.block(0, m, m, n);
    Eigen::MatrixXd Arm = A.block(m, 0, n, m);
    Eigen::MatrixXd Arr = A.block(m, m, n, n);
    Eigen::VectorXd brr = b.segment(m, n);
    A = Arr - Arm * Amm_inv * Amr;//这里的A和b应该都是marg过的A和b,大小是发生了变化的
    b = brr - Arm * Amm_inv * bmm;

残差

    //下面就是更新先验残差项
    Eigen::SelfAdjointEigenSolver saes2(A);//求特征值
    Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
    Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));

    Eigen::VectorXd S_sqrt = S.cwiseSqrt();
    Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();

    linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
    linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;