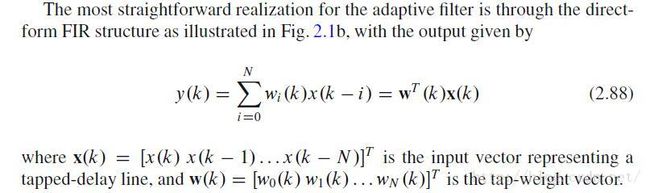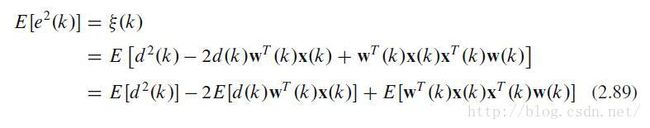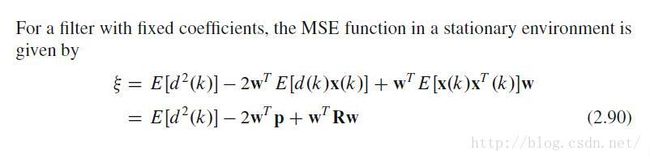滤波器设计(3):维纳(Wiener)滤波器的设计
引言
通信领域中,当然完全不止通信领域,一个很常见的需求就是,从含有噪声,或是已经畸变的信号中,
提取出或恢复出原始的、有用的信号。怎么做?可以用滤波器(Filter)。滤波器的变量(输入)是信号,
信号又是时间or空间or时间空间or…的函数。于是,函数的函数——泛函。至今,我没有学过,唉……
一定要抽时间学一下“泛函分析”……%>_<%
关于滤波器的设计,在大学本科开设的“电路原理”、“模拟电子技术基础”、“信号与系统”等课程中,或多或少
要涉及一点,但好像基本上都是一些经典滤波器。比如LPF、HPF,……,IIR、FIR……
前面的文章里,有一些对IIR、FIR滤波器的回顾。
Review: IIR滤波器的设计
Review: FIR滤波器的设计
对于滤波效果的评判标准有很多,这个问题没有标准答案。
客观而言,均方误差最小,均方离差(绝对误差)最小等。
主观而言,看起来效果变好了?听起来效果变好了?
其实,就连听起来效果变好了,这种话也是非常非常非常不严格的。
比如,有些人就喜欢重低音的鼓点,有些人就是喜欢清晰的人声。
所以,实际效果还真的就是因人而异了。
实际上(“实际上”,“事实上”的意思,就是提醒读者注意,后面即将要出现重要的内容了!),
在平均平方误差(mean square error)的意义下,经典滤波器常常不能达到“最优”。
所以,更进一步,用现代滤波器做信号处理。但是,通常,这是以“先要知道信号的一些统计特性”为代价的。
于是,维纳(Wiener)滤波器,闪亮登场。其实,在学维纳滤波器之前,应该先有一些随机过程的基本概念。
维纳滤波器简介
以下摘自百度百科。
维纳滤波器(Wiener filter)是由数学家维纳(Rorbert Wiener)提出的一种以最小平方为最优准则的线性滤波器。在一定的约束条件
下,其输出与一给定函数(通常称为期望输出)的差的平方达到最小,通过数学运算最终可变为一个托布利兹方程的求解问题。维纳滤波器又被称为最小二乘滤波器或最小平方滤波器,目前是基本的滤波方法之一。维纳滤波是利用平稳随机过程
的相关特性和频谱特性对混有噪声的信号进行滤波的方法,1942年美国科学家N.维纳为解决对空射击的控制问题所建立,是40年代在线性滤波理论方面所取得的最重要的成果。
更加详细的信息可参考百度百科的词条 维纳滤波器。
另外,维纳滤波器应该是一个FIR滤波器。
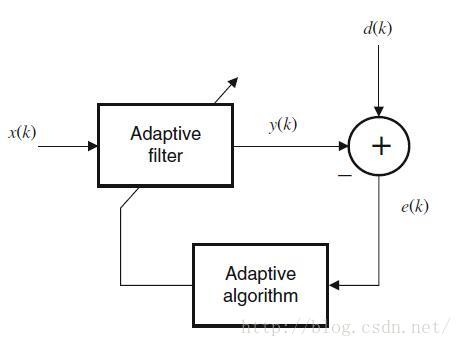
自适应滤波器(adaptive filter)基本框图如下。
自适应滤波器后面会讲。跟自适应滤波器不同的地方就是,维纳滤波器好像是没有反馈的吧……
所以维纳滤波器的框图,就是把下图的反馈环路去掉,同时滤波器的系数不可变。自适应的是可以通过反馈回来的e进行系数调整。
x是滤波器的输入,y是滤波器的输出。输出与一个参考信号(期望信号)d作差,得到误差信号e。
注意事项
刚开始接触这一类滤波器的时候,我总是不知道这个参考信号d是什么情况。
有些书上会把d说出期望信号。我就在想,既然都能知道所期待的输出信号是什么了,为什么还要去滤波?
这不简直就是“脱了裤子放屁——多此一举”吗?
我相信有很多人跟我一样,初学的时候会觉得真的很奇怪。
有些书根本就回避了这个至关重要的问题。我只能说,也许作者是真的很懂,以至于不知道我们这些初学者什么不懂。好惨。
其实,这里面好像是有个“训练”,或者叫“预先测试”的过程。我把它叫A阶段,同时,把真正工作的阶段叫B阶段。
在预先测试的过程中,要做的工作是去求滤波器的系数w;而一旦预先测试过程结束,滤波器真正开始工作了,其系数就不改变了。
以我现在的认知水平,维纳滤波器的逻辑是这样的。
1. 在预先测试的过程中,期望信号d是可以知道的。x是可以获取的。因此,可以求出滤波器的系数w。
2. 在后来真正运行的过程中,就拿着这个w,去处理可以获取的x。x可能是含噪信号,可能是畸变信号,等等。
处理后,会输出y。这就是处理过后的信号,也许是滤除噪声的,也许是信道均衡后的,也许是恢复过后的,等等。
一个例子
假设现在在一个很吵的环境中,要用话筒录音,那不可避免会录入噪声。如何去除噪声?
除了用经典滤波器外呢,如果要求用维纳滤波器呢?
我个人的做法会是这样。
A. 预先测试过程
1. 找一段所谓的干净的语音,作为d。假设就是在安静的录音棚里录下来的。先准备着。
2. 播放干净的d,用话筒把它录音,录下来。因为有了噪声,所以变成了含噪信号x。我也拿到了。
3. 用x和d,去计算滤波器系数w。
B. 真正录音阶段
1. 演员登场,真正的录音开始了。这是能够录到含噪信号x。
2. 用A阶段得到的w,去处理这时录到的x。此时,应该说,输出的y,就是降噪以后的信号了。
当然,感觉上,A阶段所准备的干净语音,如果就是B阶段中,真正要说话的那个人的声音,按理说,效果可能会好一些。
基本原理
原理的话,就是希望在A阶段,找一组滤波器系数w,让滤波器的输出y和期望信号d之间的均方误差最小。
后来均方误差是关于w的一个二次型,所谓的二次曲面,有唯一的极小值,同时也是最小值。
然后就是一堆求偏导数,求最值。同时,令各个偏导导函数为0,求出驻点,也是极值点,也是最小值所在的自变量w所在的位置。
利用随机过程里的一些式子,再假定什么x宽平稳,再用相关函数的定义之类的一些东西,
从而得到一个Wiener-Hoff方程。(Ax = b类型的非齐次线性方程组,此x非上文的x。单纯是线性代数中的Ax=b那个x)
方程中的A,是收集到的,待处理信号x的自相关阵,也是一个Hermitian对称阵,还是一个托普利兹(
Toeplitz)矩阵。如果x是实信号,那就是对称矩阵。半正定,等等性质。
方程中的x,是要求的维纳滤波器的系数w。
方程中的b,就是要求的期望信号d和待处理信号x之间的互相关阵。
最后,算这个方程就是了。
至于,w阶数取多少,这个嘛,我反正目前只知道,“试”。trail and error。
下面摘了一些资料过来。
扩展应用
后面会有维纳滤波器的实例代码。今天就写这么多。