趣味数学问题的算法实现
一.袋鼠跳跃问题
问题描述:
有一只袋鼠,它跳跃一次的方式只有两种:①一次跳1米 ②一次跳3米,现在有一段10米长的路,袋鼠从起点开始跳,问到终点有多少种不同的跳跃方式?
问题分析:
10米其实通过枚举就能够计算出来,但是我们要做的是给出计算任何距离的算法,从而得到一个普遍的结论。
如果没有看出规律,可以一步一步分析。首先我们设剩余的距离为n,对应的不同跳跃方式为f(n)种,袋鼠肯定要跳第一次,有两种跳法,1米和3米,跳过以后的方式加一起等于f(n),即f(n)=f(n-1)+f(n-3),第二次跳又有两种方式,如此递归,最后对剩下的路程做判断,如果剩下1米,则只有一种方式,2米同样,3米则有两种方式。
算法实现:
#define N 10
int f(int n)
{
int m;
if(n==1||n==2) m=1;
if(n==3) m=2;
if(n>3) m=f(n-1)+f(n-3);
return m;
}
main()
{
printf("%d: %d\n",N,f(N));
}运行结果如下:
可以手动验算一下,结果是正确的,我们变换N的取值,结果也都是可靠的。这个算法是采用递归调用实现的,但是递归调用涉及到栈的进出,耗费大量时间,所以效率不高,可以采用循环的方式进行,就是将递归放到循环中,此处不给出算法了。
二. 数字反转问题
问题描述:
有一个四位数,它的各位数字翻转以后组成新的四位数,原来的四位数是新四位数的4倍,求这个四位数。
问题分析:
本题涉及到各个位上数字的拆分和重组,所以要用到常见的数字拆分的算法,然后用数组盛装,再进行重组,最后判断并输出。
算法实现:
#define N 4
main()
{
int i,a,b,n,t,k,m;
short s[N];
for(i=0,a=1;i1;i++) a*=10; b=a*10;
for(n=a;n0; do{s[i++]=t%10; t/=10;} while(t); //①
for(i=N-1,k=1,m=0;i>=0;i--) {m+=s[i]*k; k*=10;}
if(n==4*m) printf("%d = 4 * %d\n",n,m);
}
} 运行结果如下:
程序中的①处用到了标准的拆分数字的算法do{s[i++]=t%10; t/=10;} while(t);是采用原数依次除以10,得到的余数即为原数的各位数字。
三. 数学黑洞问题
问题描述:
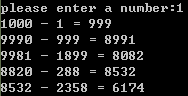
任给出一个四位以内的数k0,用它的各位数字由大到小重新排列成一个数m,再减去它的反序数rev(m),得出数k1=m-rev(m),然后,继续对k1重复上述变换,得数k2.如此进行下去,可以发现,无论k0是多大的数, 只要各位数字不全相同,最多进行7次上述变换,就会出现四位数6174,也就是数学黑洞。
问题分析:
本题与上一题基本类似,只是在未知最后结果是6174的情况下,不能在程序中出现有关6174的声明,所以需要声明一个flag用来标记是否两次的运算结果相同,因为6174按上述运算一次的结果还是6174。
算法实现:
#define N 4
main()
{
int i,fg,t,n,j,a,b,c,k; short s[N];
printf("please enter a number:");
scanf("%ld",&n);
do
{
i=fg=0; t=n;
do{s[i++]=t%10; t/=10;} while(t);
for(j=i;js[i]=0;
for(i=0;i1;i++)
for(j=i+1;jif(s[i]<s[j])
{
t=s[i]; s[i]=s[j]; s[j]=t;
}
}
for(i=N-1,a=0,b=0,k=1;i>=0;i--)
{
a+=s[i]*k;
b+=s[N-i-1]*k;
k*=10;
}
c=a-b;
if(c!=n)
{
printf("%d - %d = %d\n",a,b,c);
n=c;
fg=1;
}
}
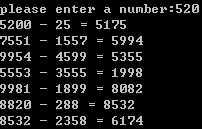
while(fg);
} 以上是几个与数学问题相关的算法实现,几乎所有数学问题都可用计算机来模拟解决,日常关注这些数学问题并思考如何用算法解决是一件很有趣的事。