MADDPG翻译

论文全称：Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments
项目地址： https://blog.openai.com/learning-to-cooperate-compete-and-communicate/

本文是对MADDPG的翻译，huanghe

摘要

我们研究了将深度强化学习用于多智能体领域。首先，我们分析了传统的算法用于多智能体环境下的困难：Q-learning会受到环境不稳定性的挑战，而policy gradient方法在智能体数目增多时，会有variance变大的问题。因此，我们提出了一个actor-critic方法的变种，在考虑其他智能体的action policy的同时，能够成功地学到多智能体的协同policy。另外，我们还引入了一种训练规则，它集成了各个智能体的policy，来得到一个更加鲁棒的多智能体policy。我们展示了我们的方法相比现存方法在既合作又竞争的环境下的优势，在这种环境下， 智能体群体能够发现各种物理和信息层面上的合作策略。

一， 引言

强化学习（RL）近来被应用到解决许多挑战性问题上去， 比如玩游戏和机器人上。在工业应用中， RL可以作为大型系统的有效组成部分，比如用于数据中心的冷却。大多数RL的成功应用都时在单智能体场景下， 在此场景下，无须建模与预测环境中其他行为体。

但是，也有很多重要的应用场景牵涉到多个智能体之间的交互，在这种共同的交互演化过程中，会有新的行为出现，问题也会变得更加复杂。 比如说，多个机器人的控制，语言的交流，多玩家的游戏，以及社会困境的分析，这些都是多智能体的场景。相关的问题，比如层级强化学习(hierarchical reinforcement learning)也可以视作多智能体的系统，因为多个层级就可以等价视作多个智能体。另外，多智能体自我对弈（self-play）最近也被表明是一个有效的学习范式。成功地把强化学习扩展到多智能体的环境下对于建造能够与人类或者智能体之间互相交互的智能系统非常重要。

不幸的是，传统的RL方法，比如Q-Learning或者policy gradient都很不适用于多智能体环境。一个问题是，在训练过程中，每个智能体都在变化，而且每个智能体的角度来看，环境都会变得不稳定（以一种智能体自己的policy无法解释的方式）。这给训练稳定性带来了挑战，并且阻碍了直接利用先前的经验重放（原文是experience replay，其实就是off-policy中常用的一种数据去相关的方法），这对于稳定深度Q-learning至关重要。另一方面，policy gradient方法，在要求多智能体协作的时候通常会有很高的方差（variance）。或者，可以使用基于模型的策略优化，其可以通过反向传播学习最优策略，但是这需要世界动力学的一个（可微分）模型和关于智能体之间相互作用的假设。将这些方法应用于竞争环境也是优化的挑战从对抗训练方法的臭名昭着的不稳定就可以看出这一点。

在这项工作中，我们提出了一个通用的多智能体学习算法：（1）可以学习到在执行时只使用本地信息（即它们自己的观察）的策略，（2）不假设环境动力学的可微模型或智能体之间通信方法的任何结构，（3）不仅适用于合作交互而且适用于涉及物质和信息行为的竞争或混合交互环境（指合作和竞争的混合环境）。能够在合作竞争的混合环境中行动的能力对智能体来说可能是至关重要的；虽然竞争性训练提供了一个自然的学习条件[30]，智能体也必须在执行的时候展示出合作的行为（例如与人类）。

我们采取分散执行，集中训练的框架，使policy能使用额外的信息来缓解训练压力，只要这些信息在测试时间没有使用。Q-learning是天然无法胜任，如果不对环境做一些额外的结构上的假设，因为Q函数一般来说是不能在训练和测试的时候包含不同的信息的。因此，我们提出了一种 actor-critic policy gradient方法的简单的扩展，critic增加了其他智能体的policy的额外信息，actor则只能接触到本地的信息（也就是该智能体自身的）。训练完成后，只有local actor在执行阶段使用，以分散的方式执行，同样适用于合作和竞争环境。由于集中的critic函数明确地使用了其他智能体的policy，我们额外地展示了智能体可以在线学习其他代理人的近似模型并有效地用到他们自己的policy学习过程中去。我们还会介绍一种提高多智能体policies稳定性的方法，通过policies的集成，因此这需要强有力的互动与各种合作者和竞争对手的policy。我们通过实验显示出我们方法相比现有的方法在合作以及竞争的环境下的优越性，在这种环境下，智能体群体能够发现复杂的物理和交流协调策略。

二， 相关工作

多智能体设置下，最简单的学习方法是独立使用可学习的智能体。这曾经被文献[34]使用Q-learning尝试，但是在实际中效果并不好。正如我们将要展示的那样，独立学习的policy gradient方法也表现不佳。一个问题是，在训练过程中，每个智能体的policy都会发生变化，从而导致非固定的环境，并妨碍经验的重复应用（expericen replay）。以前的工作试图通过输入其他智能体的policy参数来解决这个问题，将迭代索引显式地添加到重放缓冲区，或使用重要性采样[9]。以前深入的Q-learning方法已经在文献[33]中进行了研究，以训练相互竞争的Pong智能体。

智能体之间的相互作用的本质可以是合作的，竞争的，或者两者兼而有之。很多算法只针对某一种特定的交互方式进行了设计。大多数研究是合作的设置，如乐观和滞后的Q函数更新策略[15,21,25]，其中假设其他智能体的行为是为了提高集体回报。另一种方法是通过共享policy的参数间接达成合作[12]，但这需要同质化智能体的能力。这些算法通常不适用于竞争或竞争合作的混合设置。参见[26,4]了解有关多智能体学习方法和应用的调研。

与我们的工作同时，[7]提出了一个类似的想法，使用policy gradient的方法以及集中的critic，并在星际争霸的微观控制任务上测试了他们的方法。他们的方法在以下方面与我们有所不同：（1）他们为所有的智能体只学习了一个单一的中央critic，而我们为每个智能体都学习了一个集中的critic，这允许具有不同奖励函数的智能体，包括在竞争环境下（2）我们考虑了智能体之间有明确通信的环境，（3）他们将周期性policy与前馈critic结合起来，而我们的实验则是使用前馈policy（虽然我们的方法适用于周期性policy），（4）我们学习的是连续的policy，而他们学习的是离散的。

最近的工作集中在学习智能体之间的基础协作通信协议以解决各种任务[29,8,24]。但是，这些方法通常只适用于以下情况，也即智能体之间的通信是通过专用的，可微分的通信通道进行的。

我们的方法需要明确地建模其他智能体的决策过程。这种建模的重要性已经被强化学习[3,5]和认知科学群体所认识到[10]。 [13]强调了对其他智能体决策过程鲁棒的重要性，就像其他人一样通过建立贝叶斯决策模型。我们也吸收了这种鲁棒性的考量，通过要求智能体与任何其他智能体的可能的policy的集成进行交互来实现，这提高了智能体的训练过程中的稳定性和训练后的鲁棒性。

三， 研究背景

马尔可夫博弈 在这项工作中，我们考虑马尔可夫决策过程的多智能体扩展（MDPs），称为部分可观察马尔可夫博弈[19]。 N N 个智能体的马尔可夫博弈定义为描述所有智能体的可能配置的一组状态 S S ，动作 A1,...,AN A 1 , . . . , A N 和每个智能体的观测值 O1,...,ON O 1 , . . . , O N 。当选择action时，每个智能体使用随机policy πθi：Oi×Ai↦[0,1] π θ i ： O i × A i ↦ [ 0 , 1 ] ，根据状态转移函数产生下一个状态 T：S×A1×...×AN↦S2 T ： S × A 1 × . . . × A N ↦ S 2 。每个智能体都根据状态和动作获得reward， ri：S×Ai↦R r i ： S × A i ↦ R ，并收到与各自状态相关的观测值： oi:S↦Oi o i : S ↦ O i 。初始状态由分布 ρ ρ 确定： S↦[0,1] S ↦ [ 0 , 1 ] 。每个智能体旨在最大化自己的总预期回报 Ri=∑Tt=0γtrti R i = ∑ t = 0 T γ t r i t ，其中 γ γ 是折扣因子， T T 是时间范围。

Q-Learning和深度Q网络（DQN） Q-Learning和DQN [23]是很流行的强化学习，并已被应用于多智能体环境[8,35]。 Q-Learning利用的动作值函数 Qπ(s,a)=E[R|st=s,at=a] Q π ( s , a ) = E [ R | s t = s , a t = a ] 来生成policy π π 。这个Q函数数可以递归地重写为 Qπ(s,a）=Es′[r(s,a)+γEa′∼π[Qπ(s′,a′)]] Q π ( s , a ） = E s ′ [ r ( s , a ) + γ E a ′ ∼ π [ Q π ( s ′ , a ′ ) ] ] 。 DQN通过最小化损失来学习到最优policy对应的动作值函数 Q∗ Q ∗

                                 L(θ)=Es,a,r,s′[(Q∗(s,a|θ)−y)2]                                                                   L ( θ ) = E s , a , r , s ′ [ ( Q ∗ ( s , a | θ ) − y ) 2 ] ，其中 y=r+γmaxa′Q¯∗(s′,a′) y = r + γ m a x a ′ Q ¯ ∗ ( s ′ , a ′ )

其中Q是目标Q函数，其参数用最新的 θ θ 的周期性地更新，这有助于稳定训练。稳定DQN的另一个重要组成部分是使用一个经验重放缓冲区 D D ，它包含元组 (s,a,r,s′) ( s , a , r , s ′ ) 。Q学习可以直接应用于多智能体设置，让每个智能体学习一个独立的最优函数 Qi Q i [34]。但是，因为智能体随着学习的进展独立地更新他们的policy，从任何一个智能体的角度来看，环境都会变得不固定，这违反了Q学习收敛所需的马尔可夫假设。另一个在[9]中观察到的困难是，经验重放缓冲区不能用于这样的多智能体设置，因为一般来说，当 πi≠π′i π i ≠ π i ′ 时， P(s′|s,a,π1,...,πN)≠P(s′|s,a,π′1,...,π′N) P ( s ′ | s , a , π 1 , . . . , π N ) ≠ P ( s ′ | s , a , π 1 ′ , . . . , π N ′ ) 。

策略梯度（PG）算法 策略梯度方法是各种RL任务的另一个选择。主要思想是直接调整策略的参数 θ θ 以便于通过沿 ∇θJ(θ) ∇ θ J ( θ ) 的方向进行前进来最大化目标 J(θ)=Es∼pπ,a∼πθ[R] J ( θ ) = E s ∼ p π , a ∼ π θ [ R ] 。运用先前定义的Q函数，策略的梯度可以如[32]一样写成：

                                             ∇J(θ)=Es∼pπ,a∼πθ[∇θlogπθ(a|s)Qπ(s,a)]                                                                                           ∇ J ( θ ) = E s ∼ p π , a ∼ π θ [ ∇ θ l o g π θ ( a | s ) Q π ( s , a ) ]

其中 pπ p π 就是状态分布。策略梯度定理启发了几个实际算法，它们经常在估计 Qπ Q π 的方式上不同。例如，可以简单地使用一个样本返回 Rt=∑Ti=tγi−tri R t = ∑ i = t T γ i − t r i ，这就是REINFORCE算法[37]。或者，也可以通过TD learning来学习真实动作值函数的近似函数 Qπ(s,a) Q π ( s , a ) [31];这个 Qπ(s,a) Q π ( s , a ) 被称为批评者，并演化出了各种各样的actor-critic算法[31]。

众所周知，策略梯度方法会有高方差梯度估计。这在多智能体设置中更加加剧了；因为智能体的reward通常取决于许多智能体的动作，只有智能体自己的动作（当智能体的优化过程中没有考虑到其他智能体的动作时）的reward表现出更多的可变性，从而增加了其梯度的方差。下面，我们展示一个简单的设定，在此设定下梯度更新往正确方向前进的概率随着智能体的数量呈指数下降。

命题1. 考虑具有二元行为的N个智能体： P(ai=1)=θi P ( a i = 1 ) = θ i ，其中 R(a1,...,aN)=1a1=...=aN R ( a 1 , . . . , a N ) = 1 a 1 = . . . = a N 。我们假设一个不知情的情景，其中智能体被初始化为 θi=0.5,∀i θ i = 0.5 , ∀ i 。然后，如果我们用策略梯度估计成本 J J 的梯度，我们有：

                                           P(<∇^J,∇J>>0)∝(0.5)N                                                                                       P ( < ∇ ^ J , ∇ J >> 0 ) ∝ ( 0.5 ) N

其中， ∇^J ∇ ^ J 是单样本的策略梯度估计，而 ∇J ∇ J 则是真实的梯度。

证明见附录。

基线的使用，由于前面提到的非平稳性问题，那些通常用于缓解高方差的价值函数基线，在多智能体的环境下是有问题的。

确定性策略梯度（DPG）算法 也可以将策略梯度框架扩展到确定性策略 μθ:S↦A μ θ : S ↦ A 。特别是在一定的条件下，我们可以把目标函数 J(θ)=Es∼pμ[R(s,a)] J ( θ ) = E s ∼ p μ [ R ( s , a ) ] 的梯度写成：

                                       ∇J(θ)=Es∼D[∇θμθ(a|s)∇aQμ(s,a)|a=μθ(s)]                                                                               ∇ J ( θ ) = E s ∼ D [ ∇ θ μ θ ( a | s ) ∇ a Q μ ( s , a ) | a = μ θ ( s ) ]

由于这个定理依赖于 ∇aQμ(s,a) ∇ a Q μ ( s , a ) ，它需要动作空间 A A （策略 μ μ 也一样）连续。

深度确定性策略梯度（DDPG）是DPG的变体，其中策略 μ μ 和批评 Qμ Q μ 用深度神经网络近似。 DDPG是一个off-policy策略算法，并从存储在整个训练过程中的重放缓冲中采样样本轨迹。 DDPG也使用了目标网络，如DQN [23]。

四， 方法

4.1 多智能体Actor Critic

我们在前面的章节中曾经论证过，朴素的policy gradient方法在简单的多智能体环境下表现不佳，这在第5节的实验中得到了验证。我们在本节中的目标是推导出一个在这样的环境下运行良好的算法。但是，我们希望算法在以下约束条件下运行：（1）学习的策略只能在执行时只能使用本地信息（即它们自己的观察结果），（2）与[24]不同，我们无需知道环境的可微分动力学模型（3）我们对智能体之间的通信方法不做任何结构上的假设（即，我们不假设一个可区分的通信渠道）。 一旦满足上述要求，那么将产生一个通用的多智能体学习算法，不仅可以应用于具有明确通信渠道的合作博弈，还可以应用竞争性博弈和只涉及主体之间物理交互的博弈。

与[8]类似，我们通过采用分散执行，集中训练的框架来实现我们的目标。 因此，我们允许策略使用额外的信息来简化训练，只要这些信息在测试时不被使用。 在Q-learning中是不可以这么做的，因为Q函数在训练和测试时通常不能包含不同的信息。 因此，我们提出了一个actor-critic策略梯度方法的简单扩展，critic增加了关于其他智能体策略的额外信息。

具体地说，考虑policy由 θ={θ1,...,θN} θ = { θ 1 , . . . , θ N } 参数化的具有N个智能体的博弈，令所有智能体策略的集合为 π={π1,...,πN} π = { π 1 , . . . , π N } 。 那么我们可以写出智能体 i i 的期望收益的梯度， J(θi)=E[Ri] J ( θ i ) = E [ R i ] 如下：

                                  ∇θjJ(θi)=Es∼pμ,ai∼πi[∇θilogπi(ai|oi)Qπi(x,a1,...,aN)]                                                                     ∇ θ j J ( θ i ) = E s ∼ p μ , a i ∼ π i [ ∇ θ i l o g π i ( a i | o i ) Q i π ( x , a 1 , . . . , a N ) ]

这里 Qπi(x,a1,...,aN) Q i π ( x , a 1 , . . . , a N ) 是一个集中的动作值函数，它将所有智能体的动作 a1,...,aN a 1 , . . . , a N ，加上一些状态信息 x x 作为输入，然后输出智能体 i i 的 Q Q 值。 在最简单的情况下， x x 可以包含所有智能体的观测值， x=(o1,...,oN) x = ( o 1 , . . . , o N ) ，但是如果允许的话，我们也可以包含附加的状态信息。 由于每个 Qπi Q i π 是分开学习的，智能体可以有任意的奖励方式，包括在竞争环境中相互冲突的奖励。

我们可以将上述想法扩展到确定性策略。 如果我们现在考虑 N N 个策略 μθi μ θ i ，参数为 θi θ i （缩写为 μi μ i ），那么梯度写成：

                                   ∇θiJ(μi)=Ex,a∼D[∇θiμi(ai|oi)∇aiQμi(x,a1,...,aN)|ai=μi(oi)]                                                                       ∇ θ i J ( μ i ) = E x , a ∼ D [ ∇ θ i μ i ( a i | o i ) ∇ a i Q i μ ( x , a 1 , . . . , a N ) | a i = μ i ( o i ) ]

经验重放缓冲区 D D 包含元组 (x,x′,a1,...,aN,r1,...,rN) ( x , x ′ , a 1 , . . . , a N , r 1 , . . . , r N ) ，记录了所有智能体的经验。集中的动作值函数 Qμi Q i μ 按如下方式更新：

                L(θi)=Ex,a,r,x′[(Qμi(x,a1,...,aN)−y)2],y=ri+γQμ′i(x′,a′1,...,a′N)|a′j=μ′j(oj)                                 L ( θ i ) = E x , a , r , x ′ [ ( Q i μ ( x , a 1 , . . . , a N ) − y ) 2 ] , y = r i + γ Q i μ ′ ( x ′ , a 1 ′ , . . . , a N ′ ) | a j ′ = μ j ′ ( o j )

其中 μ′={μθ′1,...,μθ′N} μ ′ = { μ θ 1 ′ , . . . , μ θ N ′ } 是具有延迟参数 θ′i θ i ′ 的目标策略集合。 如第5节所示，我们发现具有确定性策略的集中式critic在实践中运作良好，我们称之为多智能体深度确定性策略梯度（MADDPG）。 我们在附录中提供了完整的算法描述。

MADDPG背后的一个主要动机是，如果我们知道所有智能体采取的行动，即使策略发生变化，环境也是稳定的，因为对于任何 πi=π′i π i = π i ′ ，有 P(s′|s,a1,...,aN)=P(s′|s,a1,...,aN,π′1,...,π′N) P ( s ′ | s , a 1 , . . . , a N ) = P ( s ′ | s , a 1 , . . . , a N , π 1 ′ , . . . , π N ′ ) 。 只要我们没有像大多数传统的RL方法那样，明确地以其他智能体的行为作为条件，那么就没关系。

注意到我们在方程6中需要用到其他智能体的策略进行更新。知晓其他智能体的观测值和策略并不是特别严苛的假设; 如果我们的目的是训练智能体展现出在模拟环境下的复杂通信行为，那么这些信息通常可供所有智能体使用。 但是，如果有必要的话，我们可以放松这个假设，通过从观测中学习其他智能体的策略——我们将在4.2节描述了一个这样做的方法。

4.2 推理其他智能体的策略

为了去掉式6要求的需要知道其他智能体策略的假设，每个智能体可以额外保有一个与智能体 j j 的真实策略 μj μ j 有关的近似值 μ^ϕji μ ^ ϕ i j ，（其中 ϕ ϕ 是近似值的参数；此后简写为 μ^ji μ ^ i j ）。 这个近似策略通过最大化智能体 j j 的动作对数概率加上一个熵正则化项来进行学习：

                                           L(ϕji)=−Eoj,aj[logμ^ji(aj|oj)+λH(μ^ji)]                                                                                       L ( ϕ i j ) = − E o j , a j [ l o g μ ^ i j ( a j | o j ) + λ H ( μ ^ i j ) ]

其中 H H 是策略分布的熵。用近似的策略，方程6中的 y y 可以用如下计算的近似值 y^ y ^ 代替：

                                       y^=ri+γQμ′i(x′,μ^′1i(o1),...,μ′i(oi),...,μ^′Ni(oN)),                                                                               y ^ = r i + γ Q i μ ′ ( x ′ , μ ^ i ′ 1 ( o 1 ) , . . . , μ i ′ ( o i ) , . . . , μ ^ i ′ N ( o N ) ) ,

其中 μ^′ji μ ^ i ′ j 表示近似策略 μ^ji μ ^ i j 的目标网络。注意到式7可以完全以在线方式进行优化：在更新 Qμi Q i μ ，集中Q函数之前，我们从重放缓冲区取出每个智能体 j j 的最新的样本，执行一个梯度步骤来更新 ϕji ϕ i j 。 还要注意的是，在上面的等式中，我们直接将每个智能体的行为对数概率输入到Q中，而不是采样。

4.3 策略集成的智能体

如前所述，多智能体强化学习中的一个反复的问题是由于智能体不断变化的策略而导致的环境非平稳性。竞争环境下尤其如此，因为智能体可以通过过度适应竞争对手的行为而获得很强的策略。
这样的策略是不可取的，因为它们很脆弱，当竞争对手改变策略时就可能会失败。

为了获得对竞争智能体策略变化更鲁棒的多智能体策略，我们提出了对 K K 个不同的子策略进行汇总。在每个回合的博弈中，我们为每个智能体随机地选择一个特定的子策略执行。假设策略 μi μ i 是 K K 个不同子策略的集合，子策略 k k 由 μθ(k)i μ θ i ( k ) 表示（表示为 μ(k)i μ i ( k ) ）。对于智能体 i i ，我们最大化集成的目标值：

                                       Je(μi)=Ek∼unif(1,K),s∼pμ,a∼μ(k)i[Ri(s,a)]                                                                               J e ( μ i ) = E k ∼ u n i f ( 1 , K ) , s ∼ p μ , a ∼ μ i ( k ) [ R i ( s , a ) ]

由于不同的子策略将在不同的博弈回合中执行，因此我们为智能体 i i 的每个子策略 μ(k)i μ i ( k ) 维护一个重播缓冲区Di（k）。因此，我们可以导推出集成的目标值关于 θ(k)i θ i ( k ) 的梯度如下：
                        ∇θ(k)iJe(μi)=1KEx,a∼D(k)i[∇θ(k)iμ(k)i(ai|oi)∇aiQμi(x,a1,...,aN)|ai=μ(k)i(oi)]                                                 ∇ θ i ( k ) J e ( μ i ) = 1 K E x , a ∼ D i ( k ) [ ∇ θ i ( k ) μ i ( k ) ( a i | o i ) ∇ a i Q μ i ( x , a 1 , . . . , a N ) | a i = μ i ( k ) ( o i ) ]

五， 实验

为了实施我们的实验，我们采用[24]中提出的 grounded communication environment，它由N个代理和L个地标组成，存在于一个具有连续空间和离散时间的二维世界中。智能体可以在环境中采取物理动作，并将通信行为传播给其他智能体。与[24]不同，我们并不假定所有的智能体都有相同的动作和观察步伐，或者根据相同的策略 π π 行事。我们也考虑了双方既合作（所有的智能体必须最大化共享的回报）又竞争（智能体有相互冲突的目标）的游戏。一些环境需要智能体之间的显式的通信才能获得最好的回报，而在其他环境中，智能体只能执行物理动作。我们将每个环境的详细信息提供如下：

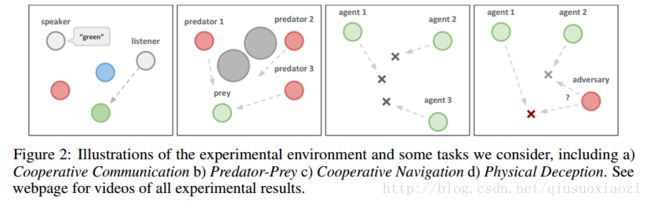
5.1 实验环境

合作交流 这个任务由两个合作的智能体组成，一个说话者和一个听众，他们被放置在三个具有不同颜色的地标的环境中。在每个回合中，听众必须导航到特定颜色的地标处，并根据其到正确地标的距离获得奖励。然而，虽然听众可以观察地标的相对位置和颜色，但它不知道它必须导航到哪个地标。相反，说话者的观察由正确的界标颜色组成，并且它可以在每个时间步骤产生一个由听众观察到的通信输出。因此，说话者必须学会根据听众的动作输出地标的颜色。虽然这个问题相对比较简单，但是正如我们在5.2节中展示的那样，它对传统的RL算法提出了很大的挑战。

合作导航 在这种环境下，智能体必须通过物理行动协作抵达 L L 个地标。智能体观察其他智能体和地标的相对位置，并根据智能体与每个地标的接近程度进行集体奖励。换句话说，智能体必须“覆盖”所有的地标。此外，智能体占据显着的物理空间，并在相互碰撞时受到惩罚。我们的智能体学着推断他们必须覆盖的地标，并在避开其他智能体的同时移动到那里。

远离 这个场景由 L L 个地标组成，包括一个目标地标， N N 个知道目标地标的合作智能体，根据他们与目标的距离给予奖励， M M 个敌对智能体必须阻止合作智能体到达目标。敌对智能体通过将智能体从地标上推开，暂时占据地标来实现这一点。虽然敌对智能体也是根据他们与目标地标的距离给予奖励，但是他们不知道正确的目标；这必须从（其他）智能体的行动中推断出来。

物理欺骗 在这里， N N 个智能体合作到达 N N 个目标地标。他们根据任何智能体到目标的最短距离得到奖励（所以只有一个智能体需要达到目标地标）。然而，一个单个的敌人也希望达到目标地标；这个问题的关键是对手不知道哪个地标是正确的。
因此，以对手距离为目标而受到惩罚的合作智能体，学着分散并占据所有地标，以欺骗对手。

捕食 在这种经典捕食猎物博弈的变体中， N N 个较慢的合作智能体必须围绕一个随机生成的环境追赶更快的对手，而 L L 个大地标阻碍了道路。每当合作智能体与对手发生冲突时，追捕的智能体就会得到奖励，而对手（也就是被捕食的智能体）则受到惩罚。捕食智能体可以观测到猎物智能体的相对位置和速度，以及地标的位置。

隐蔽的沟通 这是一个敌对的通信环境，在这个环境中，一个说话者智能体（’Alice’）必须把一个消息传递给一个监听智能体（’Bob’），而这个智能体必须在另一端重建消息。然而，一个敌对的智能体（Eve）也在观察这个信道，并且想要重构这个信息 - Alice和Bob是基于Eve的重构而受到惩罚的，因此Alice必须使用随机生成的，只有Alice和Bob知道的密钥来编码她的信息。这与[2]中考虑的密码环境相似。

5.2 与传统RL算法的比较

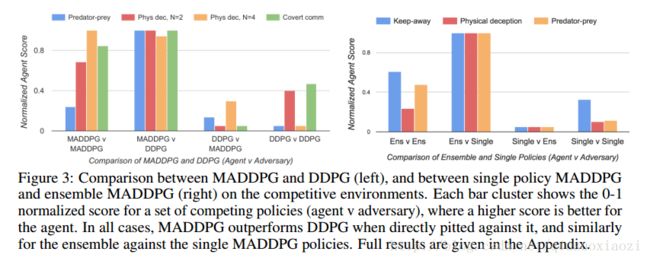
我们实现了我们的MADDPG算法，并在5.1节中介绍的环境中进行评估。除非另有说明，否则我们的策略是一个每层64个单元的双层ReLU MLP。为了支持离散的通信消息，我们使用GumbelSoftmax估计器[14]。为了评估竞争环境中学到的策略的质量，我们将MADDPG智能体与DDPG智能体进行对比，并比较智能体和对手在环境中取得的成功。我们训练我们的模型直到收敛，然后通过平均1000次迭代来进行各种度量的评估。我们在附录提供了所有环境下的结果（包括超参数）的表格和实验细节，并在这里对其进行总结。

我们首先考察合作交流情形。尽管任务简单（演讲者只需要学会输出观察结果），传统的RL方法，如DQN，Actor-Critic，TRPO的一阶实现和DDPG都不能学习到正确的行为（通过听众是否与目标地标距离很近来评估）。在实践中，我们观察到聆听者能学会忽略说话者，并简单地移动到所有观察到的地标的中间。我们绘制了图4中各种方法的25000回合以上的学习曲线。

我们猜想在这个（和其他）多智能体设置中传统RL方法失败的主要原因是缺少一致的梯度信号。例如，如果说话者在错误的方向上移动时发出正确的信号，则说话者受到惩罚。随着时间步长的增加，这个问题变得更加严重：我们观察到，传统的策略梯度方法可以学习什么时候听众的目标是简单地在一个单独的时间步骤中重构观察者，还是是否智能体和地标是固定并均匀分布的。这表明许多以前提出的短时间范围场景的多智能体方法（例如[16]）可能无法适用于更复杂的任务。

相反，MADDPG的智能体可以通过集中的批评者更容易地学习到协调的行为。在协作通信环境下，MADDPG能够可靠地学习到正确的倾听者和发言者的策略，​​并且倾听者经常（84.0％的时间）能够成功导航到目标。

类似的情况出现在物理欺骗任务上：当合作智能体接受MADDPG训练时，当 L=2 L = 2 时，在 94 94 的时间里，他们能够成功地欺骗对手（图5）。此外，对手的成功率还是相当低的，特别是当对手用DDPG训练时（ L=2 L = 2 时为 16.4％ 16.4 ％ ）。这与合作的DDPG智能体在任何情况下无法欺骗MADDPG对手的行为形成了鲜明的对比，甚至在 L=4 L = 4 时也欺骗不了其他DDPG智能体。

虽然合作导航和捕食者 - 猎物任务在成功和失败之间没有明显的分界，但在这两种情况下，MADDPG智能体都胜过了DDPG智能体。在协作导航中，MADDPG智能体与每个地标的平均距离比DDPG稍小，但由于易于协调，与DDPG智能体相比，每回合平均碰撞次数（ N=2 N = 2 时）几乎只有一半。同样，MADDPG捕食者在追逐DDPG猎物方面（ 16.1 16.1 次碰撞/回合）要比反向捕获（ 10.3 10.3 次碰撞/回合）要成功得多。

在隐蔽的通信环境中，我们发现，在重构爱丽丝的信息方面，使用MADDPG和DDPG进行训练的Bob表现超出了Eve。然而，使用MADDPG训练的Bob与DDPG相比，相对成功率更高（52.4％对比25.1％）。此外，只有使用MADDPG进行训练的Alice对她的消息进行编码之后使得Eve实现近乎瞎蒙乱猜的，随机的重构精度。学习曲线（附录中显示了一个样本图）显示，由于环境的竞争性而导致的振荡往往不能用共同的分散RL方法来克服。我们强调，我们不使用任何[2]中要求的密码学环境的技巧，包括修改Eve的损失函数，交替地训练智能体和对手，或者使用花哨的“混合和变换”前馈与卷积架构。

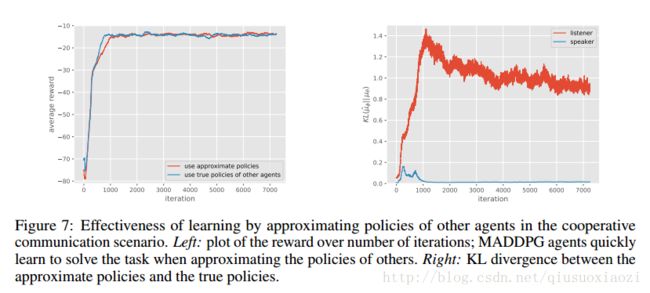
5.3 学习其他智能体策略的影响

我们评估了学习其他智能体在协作通信环境中的策略的有效性，遵循与以前的实验相同的超参数，并设置方程（1）中的 λ=0.001 λ = 0.001 。结果如图7所示。我们观察到，尽管没有完全拟合其他智能体的策略（特别是讲话者所学习的近似听众的策略与真实策略有相当大的差距），但是通过近似策略能够达到与使用真实政策相同的成功率，且不会导致收敛显著放慢。

5.4 训练集成策略的影响

我们专注于策略集合在竞争环境中的有效性，包括远离，合作导航和捕食者 - 猎物环境。我们选择 K=3 K = 3 的子策略用于远离和合作的导航环境， K=2 K = 2 用于捕食者-猎物环境。为了提高收敛速度，我们要求合作智能体在每一回合应该有相同的策略，对敌人也如此。为了评估这种方法，我们衡量了集成策略和单一策略在智能体和对手角色的表现。结果显示在图3的右侧。我们观察到，集成策略的智能体比单一政策的智能体要更加强大。尤其是，集成策略的智能体与单一策略的对手的得分（左二栏条形图）对比于角色调换后的情形（第三个左栏条形图），集成智能体的领先优势更甚。

六， 结论及未来工作展望

我们提出了一个多智能体策略梯度算法，其中智能体根据所有智能体的观测和动作来学习一个集中的critic。 从实验上看，我们的方法在各种协作和竞争的多智能体环境中胜过了传统的RL算法。 我们可以通过训练一系列集成策略的智能体，进一步提高我们方法的性能，我们相信这种方法广泛适用于任何多智能体算法。我们方法的一个缺点是，Q的输入空间随智能体个数 N N 线性增长（取决于 x x 中包含的信息）。在实践中，这可以通过，比如使用一个仅考虑一个智能体某邻域内的其他智能体的模块化Q函数来缓解。我们把这个留到未来研究。

附录部分未翻译，请参考原文