集成学习之boosting，Adaboost、GBDT 和 xgboost（三）

AdaBoost算法的解释——前向分步法与提升树(GBDT)

可以认为AdaBoost算法是模型为加法模型，损失函数为指数函数、学习算法为前向分步算法时的二类分类学习方法。

前向分步算法：

考虑加法模型$f(x)=\sum _{m=1}^M{\beta }_{m}b(x;{\gamma }_m)$ —— (式1)
其中$b(x;{\gamma }_m)为基函数，{\gamma }_m为基函数的参数，{\beta }_m为基函数的系数。$显然式1 是个加法模型。
在给定训练数据和损失函数$L(y,f(x))$的条件下，学习加法模型$f(x)$称为经验风险极小化即损失函数极小化问题：

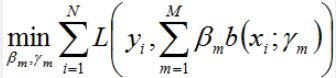
通常这是一个复杂的优化问题。前向分步算法求解这一优化问题的想法是：因为学习的是加法模型，如果能够从前往后求解，每一步只学习一个基函数及其系数，逐步逼近优化目标函数，那么就可以简化优化的复杂度。

具体的，每一步只需优化如下损失函数：

给定训练数据集$T=(x_1,y_1),(x_2,y_2)\dots \dots (x_N,y_N)$损失函数$L(y,f(x))$和基函数的集合{$b(x;{\gamma }_m)$},学习加法模型$f(x)$的前向分步算法如下：
输入：训练数据集$T=(x_1,y_1),(x_2,y_2)\dots \dots (x_N,y_N)$；损失函数$L(y,f(x))$和基函数的集合{$b(x;{\gamma }_m)$}
输出：加法模型$f(x)$

1. :初始化$f_0(x)=0$
   2)：对m=1,2……M:
   (a):极小化损失函数
   $({\beta }_m,{\gamma }_m)=argmin\sum _{i=1}^{N}L(y_i,f_{m-1}(x_i)+\beta b(x_i;\gamma ))$
   得到参数${\beta }_m,{\gamma }_m$
   (b)更新，$f_m(x)=f_{m-1}(x)+{\beta }_{m}b(x;{\gamma }_m)$
   3)得到加法模型$f(x)=f_M(x)=\sum _{m=1}^M{\beta }_{m}b(x;{\gamma }_m)$

这样，前向分步算法将同时求解从m=1到M的所有参数${\beta }_m,{\gamma }_m$的优化问题简化为逐次求解各个${\beta }_m,{\gamma }_m$的优化问题。

提升树

提升树是以分类树与回归树为基本分类器的提升方法。提升树被认为是统计学习中性能最好的方法之一。
提升树模型
提升方法实际是采用加法模型（即基函数的线性组合）与前向分步算法。**以决策树为基函数的提升方法称为提升树。**对分类问题决策树是二叉分类树，对回归问题决策树是二叉回归树。
提升树模型可以表示成决策树的加法模型：
$f_M(x)=\sum _{m=1}^{M}T(x;{\odot }_m)$,其中$T(x;{\odot }_m)表示决策树；{\odot }_m表示决策树的参数;M为树的个数$

提升树算法：

提升树采用前向分步算法，首先确定初始提升树$f_0(x)=0$,第m步的模型是
$f_m(x)=f_{m-1}+T(x;{\odot }_m)$
其中，$f_{m-1}$是当前模型，通过经验风险最小化确定下一颗决策树的参数${\odot }_m$
${\odot }_m=argmin\sum _{i=1}^{N}L(y_i,f_{m-1}(x_i)+T(x;{\odot }_m))$
由于树的线性组合可以很好的拟合数据，即使数据中的输入与输出之间的关系很复杂也是如此，所以提升树是一个高功能的学习算法。

下面讨论针对不同问题的提升树学习算法，其主要区别在于使用的损失函数不同
包括用平方误差损失函数的回归问题，用指数损失函数的分类问题呢，以及用一般损失函数的一般决策问题。

对于二类分类问题，提升树算法只需将AdaBoost算法中的基本分类器限制为二类分类器即可，可以说这时的提升树算法是AdaBoost算法的特殊情况。

下面介绍回归问题的提升树。

已知一个训练数据集$T=(x_1,y_1),(x_2,y_2),\dots \dots (x_N,y_N)$,前面已经讨论了回归树的问题
如果将输入空间划分为$J$个互不相交的区域$R_1,R_2\dots \dots R_J$，并且在每个区域上确定输出的场景$c_j$,那么树可以表示为：
$T(x;\odot )=\sum _{j=1}^J{c}_{j}I(x\in R_j)$
其中 ，参数$\odot =(R_1,c_1),(R_2,c_2)\dots （R_J,c_J）$表示树的区域划分和各区域上的常数。J是回归树的复杂度即叶子结点个数。

回归问题的提升树使用以下前向分步算法：
$f_0(x)=0$
$f_m(x)=f_{m-1}(x)+T(x;{\odot }_m),m=1,2\dots \dots M$
$f_M(x)=\sum _{m=1}^{M}T(x;{\odot }_m)$
在前向分步算法的第m步，给定当前模型$f_{m-1}(x)$,需要求解
${\odot }_m=argmin\sum _{i=1}^{N}L(y_i,f_{m-1}(x_i)+T(x;{\odot }_m))$得到
${\odot }_m$,即第m颗树的参数。
当采用平方误差损失函数时，$L(y,f(x))=(y-f(x){)}^2$其损失变为：
$L(y,f_{m-1}(x)+T(x;{\odot }_m))$
$=[y-f_{m-1}(x)-T(x;{\odot }_m){]}^2$
$=[r-T(x;{\odot }_m){]}^2$
这里$r=y-f_{m-1}(x)$ 是当前模型拟合数据的残差。所以对回归问题的提升树算法来说，只需要简单的拟合当前模型的残差。

【回归问题的提升树算法】：
输入：训练数据集
输出：提升树$f_M(x)$
1)初始化$f_0(x)=0$
2）对m=1,2，……M
a）按照$r=y-f_{m-1}(x)$计算残差：$r_{mi}=y_i-f_{m-1}(x_i)$是个向量
b)拟合残差$r_{mi}$学习一个回归树，得到$T(x;{\odot }_m)$
c)更新$f_m(x)=f_{m-1}+T(x;{\odot }_m)$
3)得到回归问题提升树
$f_M(x)=\sum _{m=1}^{M}T(x;{\odot }_m)$
（每棵回归树的获得都和前面提到的回归树构建算法一样）

梯度提升：
提升树利用加法模型与前向分步算法实现学习的优化过程，当损失函数时平方损失和指数损失时，每一步优化很简单。但对一般的损失函数而言，往往每一步优化不那么容易。
针对这一问题，提出了梯度提升算法（gradient boosting）.这是利用最速下降法的近似方法，其关键是利用损失函数的负梯度在当前模型的值
$-[\frac{\phi L(y,f(x_i))}{\phi f(x_i)}{]}_{f(x)=f_{m-1}(x)}$
作为回归问题提升树算法中残差的近似值，拟合一个回归树
(损失函数的负梯度在当前模型的值)（残差）

【梯度提升算法】：
输入：训练数据集$T$,损失函数$L(y,f(x))$
输出：回归树 $f(x)$
(1)初始化
$f_0(x)=argmin\sum _{i=1}^{N}L(y_i,c)$
(2) 对于m=1,2,……M
(a)对i=1,2,……N,计算
$r_{mi}=-\frac{\phi L(y,f(x_i))}{\phi f(x_i)}{]}_{f(x)=f_{m-1}(x)}$
(b)对$r_{mi}$拟合一个回归树，得到第m颗树的叶子结点区域$R_{mj},j=1,2\dots \dots J$
©对j=1,2……J,
计算$c_{mj}=argmin\sum _{x_i\in R_{mj}}L(y_i,f_{m-1}(x_i)+c)$
(d)更新$f_m(x)=f_{m-1}(x)+\sum _{j=1}^J{c}_{mj}I(x\in R_{mj})$
(3)得到回归树
$f(x)=f_M(x)=\sum _{m=1}^M\sum _{j=1}^J{c}_{mj}I(x\in R_{mj})$

算法第1步初始化：估计使损失函数极小化的常数值，它是只有一个根节点的树。
第2步a）计算损失函数的负梯度在当前模型的值，将它作为残差的估计，
第2步b)估计回归树叶子结点区域，以拟合残差近似值。
第2步c)利用线性搜索估计叶子结点区域的值，使得损失函数极小化。
第2步d）更新回归树
第3步得到输出最终模型f（x)