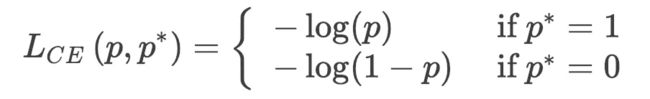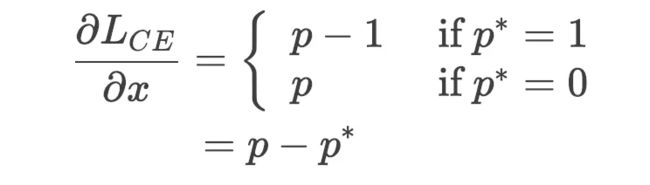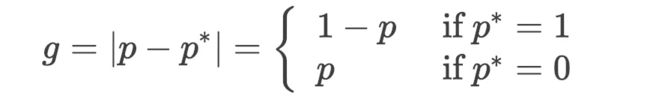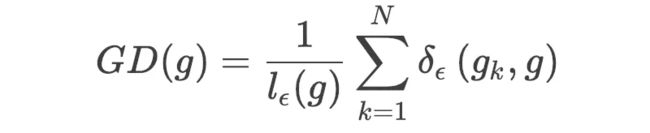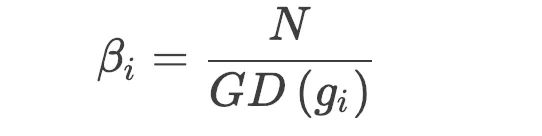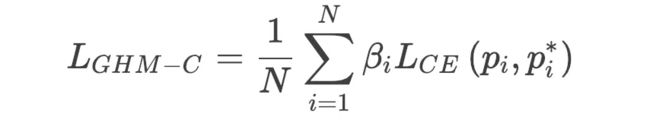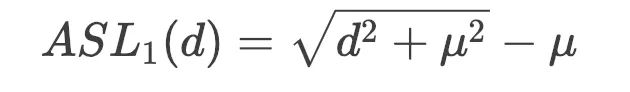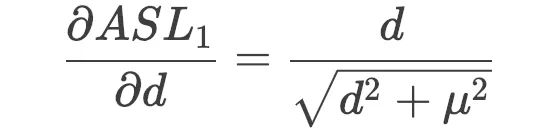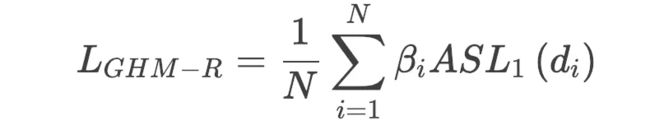Gradient Harmonizing Mechanism

目标检测方法分为两大阵营，一类是以Faster RCNN为代表的两阶段检测的方法，一类是以SSD为代表的单阶段检测方法。两阶段方法在检测精度更出色，单阶段检测方法的Pipline则更简洁，速度更快，但是精度不如两阶段检测方法，一个原因是单阶段的检测方法受限于正负样本和简单困难样本的不均衡问题，导致训练效果不佳。

为了解决这种不均衡的问题，有研究者提出了在线困难样本挖掘的方法(OHEM)，但是这个方法一方面不够高效，另一方面它只选择topN而丢弃了太多样本。后来，何凯明等提出了Focal Loss来改进cross-entropy loss, 取得了不错的效果，但是focal loss 的选择相对麻烦，因为它引入了两个超参数需要细致选择。

本文在前面研究的基础上，从梯度分布的角度，进一步指出了单阶段检测中不均衡性的本质，提出了梯度均衡化的策略来改善训练过程。

对于一个样本，如果它能很容易地被正确分类，那么这个样本对模型来说就是一个简单样本，模型很难从这个样本中得到更多的信息，从梯度的角度来说，这个样本产生的梯度幅值相对较小。而对于一个分错的样本来说，它产生的梯度信息则会更丰富，它更能指导模型优化的方向。对于单阶段分类器来说，存在着大量的负样本，可以很容易地正确分类，少量的正样本通常是困难样本。因此正负样本的不均衡性本质是简单困难样本的不均衡性。

更进一步，单个简单样本的梯度对于整个梯度的贡献很小，但是当存在大量的简单样本时，它们对梯度的贡献就不可忽略，甚至可以大于困难样本的贡献，因此导致训练过程不高效，模型没法学习到有用的信息。

基于此，作者指出难度不同样本的不均衡性可以在梯度模长的分布上体现出来。通过对梯度分布的研究，作者提出了一种梯度均衡策略可以有效地改进单阶段检测器的性能。

Gradient Harmonizing Mechanism

问题描述

对于一个候选框，它的真实标签是 , 预测的概率是，采用二元交叉熵损失： 

假设是模型输出，使得 , 那么上述的交叉熵损失对的导数是：

那么梯度的模定义为：

g的值代表了这个样本的困难程度和它对整体梯度的贡献。

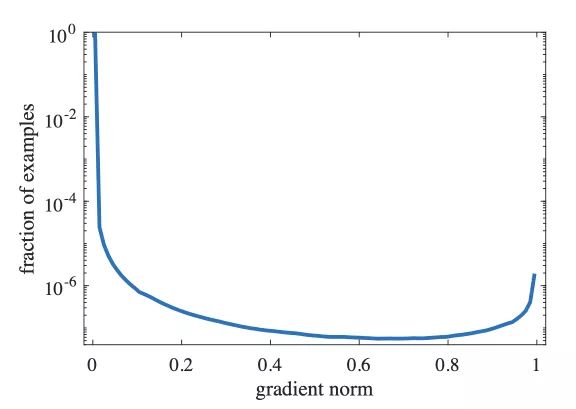
下图是一个收敛模型的梯度模长的分布，可以看出简单样本的数量很大，使得它对梯度的整个贡献很大，另一个需要的地方是，在梯度模较大的地方仍然存在着一定数量的分布，说明模型很难正确处理这些样本，作者把这类样本归为离群样本，因为他们的梯度模与整体的梯度模的分布差异太大，并且模型很难处理，如果让模型强行去学习这些离群样本，反而会导致整体性能下降。

均衡化策略

Gradient Density 
为了解决上述的梯度分布不均匀的问题，作者提出了一种均衡化的策略。大概的思路是对于梯度分布切bin，统计每一个bin内的样本数量，得到每个bin的分布，进行分布的均衡化。具体地，基于这个bin内的样本数量和这个bin的长度，可以定义梯度密度，它表示某个单位区间内样本的数量: 

要归一化整个梯度的分布，可以使用梯度密度的导数作为归一化的参数。所有对梯度进行的调整，都可以等价地变换到损失函数上，具体地，使用对样本的损失进行加权。 

GHM-C Loss
基于归一化的参数，改进cross-entropy 得到新的分类损失GHM-C Loss：

下图对比了不同损失函数下的梯度模长的分布。可以看出，之前提到的简单样本的权重得到了较大幅度地降低，离群样本也得到了一定程度的降权。使用经过改善之后的损失函数使得训练过程更加高效和鲁棒。

GHM-R Loss 

对于检测框的回归，通常都是使用 smooth L1损失： 

其中，smooth L1 损失对的梯度为：

注意到所有有较大∣d∣的样本的梯度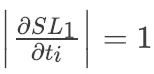，这会带来一个问题就是对于这些样本来说没有区分度，基于此作者提出了一个改进的smooth L1 loss, 称为ASL1：

这个损失函数处处可导：

定义梯度的模长为：

那么沿着上面关于分类损失的均衡化策略，同样可以得到GHM-R Loss：