Huffman树（哈夫曼树）、哈夫曼编码、最优前缀码、前缀码

目录

基本概念：

哈夫曼树的构造

哈夫曼树的应用——哈夫曼编码

附：前缀码

---

基本概念：

需要了解的一些基概念：

路径：结点序列满足是的双亲。

路径长度：路径的分支数。L=k-1

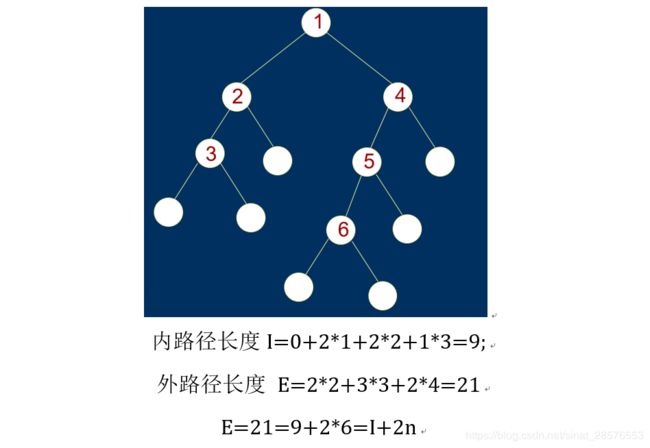
扩充二叉树：在一般二叉树中，将原来的每个空指针都指向一个特殊的结点——外结点，这样的二叉树称为扩充二叉树。

内结点——原来二叉树中的结点。

结点个数S=内结点个数+1

树的内路径长度：从根结点到各个内结点的路径长度之和。，I是二叉树的内路径长度；是一个内结点的路径长。

树的外路径长度：从根结点到各个外结点的路径长度之和。, E是二叉树的外路径长度；是一个外结点的路径长。

 

举例：

                                                                     

结点的权：有时为了表示某种含义，赋予结点一个数值。

结点加权路径长度：从根结点到该结点的路径长度与权值之积即。

树的加权路径长度：假设树的叶子有权，树中所有加权叶子结点的加权路径长度之和。【树的加权路径长度，树的带权路径长度，树的路径长度，WPL:Weighted Path Length of Tree】

其中为叶子结点的个数，为第个叶子结点的权值，为第个叶子结点的路径长度。

 

举例：

例如下图所示的具有不同带权路径长度的二叉树。                            

 

问题1：什么样的带权树路径长度最小？

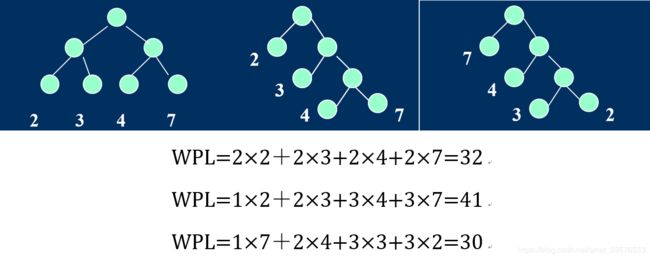
例如：给定一个权值序列{2,3,4,7}，可构造的多种二叉树的形态。

 

问题2：树的带权路径长度最小的是什么树？

Huffman树（最优二叉树） ：假设有个数据元素，它们的权值, ,….. ，以它们为叶子构造具有个叶子的二叉树（很多棵）加权长度最小的二叉树称为Huffman树。

特点：权值大的应该尽可能靠近根！

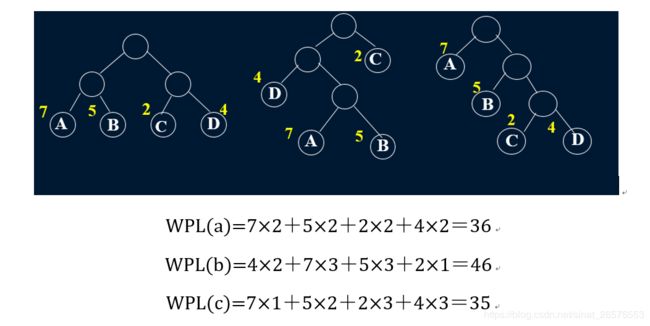
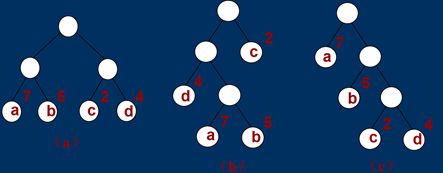
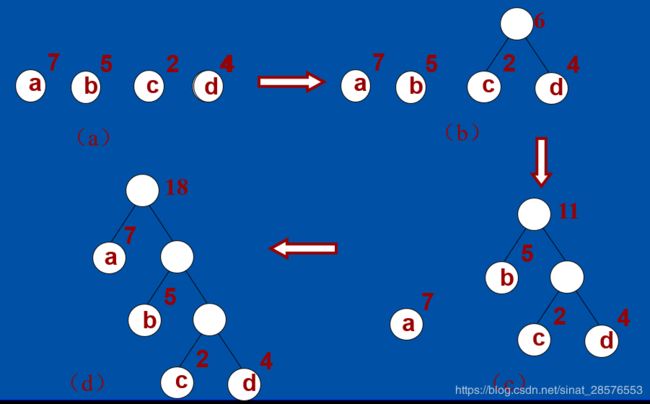
如图：三棵带权二叉树均是由分别带权7、5、2、4的4个叶子a、b、c、d构造而成，求下列二叉树的带权路径长度。

如果用WPL表示带权路径长度，则图中所示图（a）：WPL＝7×2+5×2+2×2+4×2＝36。

图（b）：WPL＝7×3+5×3+2×l+4×2＝46。

图（c）：WPL＝7×l+5×2+2×3+4×3＝35。

，其中（c）的WPL最小,其为哈夫曼树。

 

哈夫曼树的构造

基本思想：选择权值小的叶子离根距离远些。

算法：

第一步：以每个结点作为根，构造只有一个根结点的n棵二叉树，根的权值就是结点的权。

第二步：在所有二叉树中选择根的权值最小的两棵二叉树作为左右子树构造一棵新的二叉树，根的权值等于其左右子树的根的权值之和。

第三步：去掉选中的二叉树、加入新生成的二叉树。

第四步：重复2、3步，直至只剩下一棵树为止。  

 

举例：

 

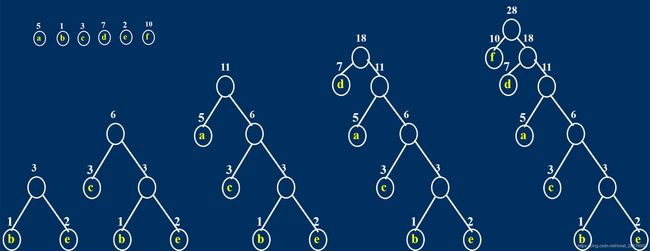
例如：有a、b、c、d、e，f 6个字符,它们的权值分别为5，1，3，7，2，10，求构造哈夫曼树。

过程如下：

 

 

哈夫曼树的应用——哈夫曼编码

 

电报是进行快捷、远距离通讯的重要手段

实现电报通讯的两个要素：

1、一套编码，可以将电文编码为待发送的电文，还可以把收到的电文，译码为原电文。

2、发送的电文尽可能短、节省线路费用。

 

编码原则：

首先，译码要唯一，即对字符进行编码后，能够唯一地翻译成原来的字符。

其次，各个字符的编码要尽可能短，只有这样才能使编码短。

注意：达到其一，很容易！    

      

当前，在主要的远距离通信手段电报通讯中，需要将要传送的文字转换成二进制的0、l组成的字符串，才能传送出去，该过程称为编码。接收方收到一系列字符串后，再把它还原成文字，即为译码。如何对不同的报文进行编码和译码才能使其报文长度达到最短，同时又能准确地对其进行编码和译码？

 

(1)每个字符使用相同长度的编码

例如，需传送的电文为“ACDACAB”，其间只用到了四个字符，则只需两个字符的串便足以分辨。令“A，B，C，D”的编码分别为“00”，“01”，“10”，“11”，则电文的二进制代码串为：“0010l10010000l”，总码长14位。接收方按两位一组进行分割，便可译码。

该方法的缺点：对出现频率不同的字符使用相同长度的编码不可能使报文长度达到最短。

 

(2)不同字符使用不同长度的编码

如果对每个字符设计长度不等的编码，且让电文中出现次数较多的字符采用尽可能短的编码，则传送电文的总长便可减少。上例电文中“A”和“C”出现的次数较多，我们可以再设计一套编码方案，即“A”，“B”，“C”，“D”的编码分别为“0”，“01”，“l”，“11”，此时电文“ACDACAB”的二进制代码串为：“011101001”，总码长为9位，显然是缩短了。

该方法的缺点：对出现频率不同的字符使用不同长度的编码可使报文长度达到最短。但是，接收方收到该代码串后无法进行译码。

若要设计长度不等的编码，必须是任一个字符的编码都不是另一个字符的编码的前缀，这种编码称为前缀编码。

 

编码的方法：哈夫曼编码的方法——不定长编码方式

前缀码：任何一个字符的编码都不是另外字符编码的前缀。

构造方法：用被编码的字符作为叶子，构造二叉树，然后在二叉树的左分支上标“0”，右分支标“1”（或反过来），每个字符的编码就是从根到该字符叶子所经路径上的0，1序列.

 

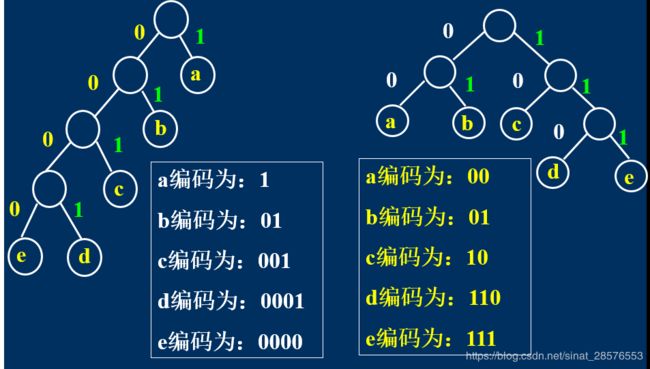
例如：有a、b、c、d、e 5个字符。

 

为什么这样构造的是前缀码？

反证法：假设不是前缀码，即一个字符编码是另一个字符编码的前缀，则从树上可以看出，从该结点又有分支发出，于是就不是叶子结点，矛盾。

如：001是0010的前缀

 

编码最短的方法——哈夫曼树（创建最优前缀码）

要使电文的编码长度最短，应该使频率高的字符，编码应该短，可以使用频率作为权值，构造编码字符为叶子的哈夫曼树（二叉树），使用频率高的字符，离根近，编码短，从而，电文编码后达到最短（而且是前缀码）。

 

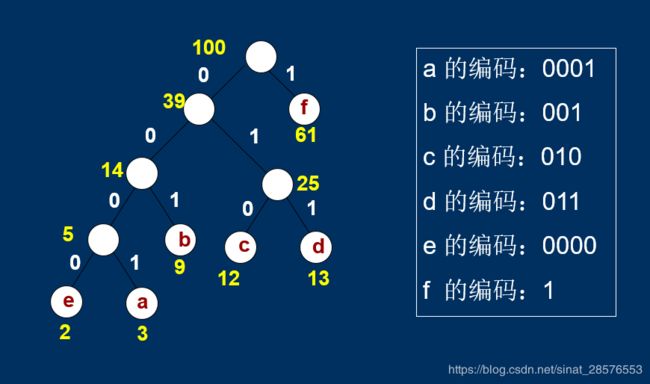
举例: 已知某系统在通信联络中只出现6个字符a、b、c、d、e、f，其在报文中出现的概率分别为0.03、0.09、0.12、0.13、0.02、0.61。试对其设计哈夫曼树，并给出哈夫曼编码及报文编码总长度。

 其报文编码总长度=(2+3)×4+(9+12+13)×3+61=183

 

附：前缀码

前置码（Prefix code），又译前缀码，是一种编码系统。这种编码系统通常是可变长度码，在其中的每个码字，都具备“前置性质”（prefix property），也就是说，在编码中的每个码字，都不能被其他码字当成前置部位。举例而言，编码字 {9, 55} 具备了前置性质，但编码字{9, 5, 59, 55}就不具备，因为其中的"5"，是"59"及"55"的前置字。这也被称为无首码的代码（prefix-free codes，PFC，无前缀码）。