基于Zynq的光流法软硬件协同设计与实现
基于Zynq的光流法软硬件协同实现
一、 前言
光流场(Optical Flow Field)[1]是指图像中所有像素点构成的一种二维(2D)瞬时速度场,其中的二维速度矢量是景物中可见点的三维速度矢量在成像表面的投影。通过光流场计算能够在相机运动以及不知道场景信息的情况下检测出运动对象。因此光流场计算方法(即光流法)在模式识别、计算机视觉以及图像处理等领域具有极其重要的基础地位。基于光流可以实现在军事航天、交通监管、信息科学、气象、医学等多个领域的重要应用。例如利用光流场可以非常有效的对图像目标进行检测和分割,这对地对空导弹火控系统的精确制导,自动飞行器精确导航与着陆,战场的动态分析,军事侦察的航天或卫星图片的自动分析系统,医学上异常器官细胞的分析与诊断系统,气象中对云图的运动分析,城市交通的车流量进行监管都具有重要价值。
光流在是由于场景中前景目标本身的移动、相机的运动,或者两者的共同运动所产生的。对光流算法的研究,真正提出有效光流计算方法还归功于Horn和Schunck [5]在1981年创造性地将二维速度场与灰度相联系,引入光流约束方程的算法,是光流算法发展的基石。在此基础上出现了大量的方法来解决这一问题:变分光流法,如Combing-Brightness-Gradient [6]、Combing-Local-Global [7];局部差分法,如Lucas-Kanade [2]、Farneback [10]; 基于特征的方法,如Wills [11]; 基于匹配的方法,如Anandan [12];基于频域的方法,如Heeger [13]; 以及基于相位的光流法:Fleet [14]。其中,变分光流法以其透明建模、旋转的不变性、稠密光流场和高质量光流场 [8] [9]成为了光流计算的首选。下面以变分光流法为主线,从计算效果和计算性能两个方面来阐述。
在研究提高光流场计算效果的过程中,Horn和Schunck [5]根据同一个运动物体的光流场具有连续、平滑的特点, 提出一个附加约束条件,将光流场的整体平滑约束转换为一个变分的问题;为了处理分段平滑的和不连续的光流场,Enkelmann [12]在Horn和Schunck的模型上引入了二次的平滑项约束; Weickert和Schnorr [15]在平滑项上引入了鲁棒性的非二次的平滑项约束以减少外部影响;同样地,在也有了非二次的数据项约束;在光照不均衡的情况下,灰度守恒不能很好的计算光流,为此Brox等人 [7]提出了梯度守恒。Lucas-Kanade [2]局部光流法的鲁棒性更好,而全局光流法计算出的是稠密光流法,因此,Bruhn等人 [7]提出了CLG的光流能量模型;为了处理较大位移的运动模型,Brox等人[8] [16]引入了一种非线性的能量守恒的能量方程。
在研究提升光流场计算性能的过程中,Black和Anandan [17]提出了由粗到精的金字塔多级结构的计算方法;Bruhn和Weickert [18]提出了多尺度的解决方法;Gwosdek [19]提出了一种线性的多尺度红黑超松弛计算方法。随着CUDA技术的发展,基于GPU的光流计算系统 [20]也受到了更多关注。由于细粒度并行支持、硬件的可重构特性及更适合嵌入式系统中实现等原因,基于FPGA的光流系统 [21] [22] [23]的高性能实现受到了最多的关注。
目前,限制光流法广泛应用的最大难题在于计算耗时,实时性差。比如常用的KLT光流法[2][3],当要处理的图像分辨率为1024*768,特征点数为1000时,在主频3GHz的P4处理器下每秒钟只能处理约2-3帧图像[4]。而稠密光流法[5][6][7],其因需要上千次迭代才能得到最优解,在现有的硬件架构下,计算相当耗时,几秒钟甚至更长时间才能处理完一幅图像,显然远远无法满足实时处理的需要。随着异构芯片的发展,Chun [24]等人认为异构芯片有优势打破传统硬件单一体系结构的局限,因此,这为光流场的实时计算提供了可能。Xilinx [25]在2012年率先推出了基于Zynq-7000的体系结构的异构芯片,集成了ARM和FPGA到一块芯片。Zynq-7000 系列器件将处理器的软件可编程能力与 FPGA 的硬件可编程能力实现完美结合,以低功耗和低成本等系统优势实现无以伦比的系统性能、灵活性、可扩展性。
本项目通过分析与研究变分光流法计算效率、硬件加速方法及最佳软硬件协作方式,在Zedboard实现上对光流场的实时计算。其中变分光流法的模型是基于Horn-Schunck [5]。如图1所示,项目实现的基本流程是:1) 先对光流算法的基本理论进行分析,包括算法的工作流程、计算复杂性、可并行性和软硬件模块的划分。2)关键接口层实现,特别是ARM与FPGA之间大数据通信的并行访问机制、高级语言对硬件结构化的描述。 3)系统设计接口层实现,比如ARM控制FPGA的IP核的初始化、配置和启动,以及软硬件协同的设计,最终基准数据测试。
二、光流算法介绍
本项目采用的光流算法是基于Horn-Schunck [5]的模型, 与Lucas- Kanade [2]光流算法相比,它算出的光流更稠密,能够精确到每一个像素点;但是它因需要求解欧拉-拉格朗日方程需要成大量的迭代,因此计算光流的时间相当耗时,比如在Zedboard的单核ARM上处理640x480的图片序列需要24.14s才能完成,这表明在传统单架构的嵌入式平台上很难满足光流场实时计算的要求。
1. 基于Horn-Schunck模型的光流算法
1.1 光流的约束条件
光流 的假设条件认为图像序列,在时间t 的某一像素点与在时间t+1的这一像素点的偏移量保持不变,即 。这就是灰度值守恒假设,通过Taylor展开,就能得到光流的约束条件(OFC): ,其中下标表示图像的梯度。
1.2 Horn-Schunck 模型
1981年,Horn和Schunck根据同一个运动物体的光流场具有连续、平滑的特点, 提出一个附加约束条件,将光流场的整体平滑约束转换为一个变分的问题。它的能量方程如下:
其中数据项表示灰度值守恒约束,平滑项表示光流平滑约束。
1.3 Euler-Lagrange方程
根据Horn-Schunck能量方程,可以推导出离散的欧拉-拉格朗日方程如下:
其中, 表示图像像素点的坐标, 表示一个像素点的上下左右四个方向的相邻的像素点,当然,在图像的边界会少于四个元素。
1.4 超松弛迭代 (SOR)
根据上面的欧拉-拉格朗日方程,不难推到出迭代方程。这里选用收敛速度最快的超松弛算法(SOR),光流的初始值是,迭代方程如下:
其中, w是迭代的权重因子, k 是迭代的次数, 是光流的计算的权值, 表示第 个像素点的上和左的相邻像素点,表示第 个像素点的下和右的相邻像素点。
2 工作流程介绍
根据上面的理论分析,可以把光流法的计算划分为四个阶段:预处理阶段(P1)、梯度计算阶段(P2)、运动模型构造阶段(P3)和迭代阶段(P5),如图2所示。
2.1 预处理阶段(P1)
这一阶段是平滑处理的图像序列,它的作用是用来减少图像噪音和外部的影响,通常用卷积来实现的。这一阶段是一个通用的图像操作。
2.2 梯度计算阶段(P2)
这一阶段是用来计算平滑好的图像的梯度,包括水平梯度、垂直梯度和时间梯度。计算梯度通常也是通过卷积来实现的。
2.3 运动模型构造阶段(P3)
这一阶段是根据计算出来的梯度来构造运动模型的信息。根据超松弛公式可以推出需要构造五个运动模型的信息,即J11、J12、J13、J22、J23。它的操作就是矩阵乘法。
2.4 迭代阶段(P4)
这一阶段就是通过超松弛算法计算光流的结果,每一次迭代完了需要把光流的信息更新一遍,再作为初始值进行下一次迭代。这一阶段的操作是根据迭代公式来实现的。
图 1 算法的工作流程
2.3 软件的执行时间
软件的实验平台是在Zedboard上ARM Cortex-A9处理器上来测试的,其中包括2个32KB 一级缓存和512KB的共享二级缓存,以及512MB的内存空间,采用的测试集下载自http://vision.middlebury.edu/flow/data/。Horn-Schunck光流算法是通过ANSI C实现的。其中迭代的次数设为100次。
基于Horn-Schunck模型的稠密光流法在软件上的执行时间如表1所示,不难发现,随着图像的不断变大,所需要的执行时间不断增大;其中迭代部分(P4)占到很大的时间比例。
Images
Size
Modules[s]
Total Time [s]
P1
P2
P3
P4
Yosemite
316x252
0.25
0.11
0.03
4.40
4.85
Venus
420x380
0.52
0.21
0.05
9.99
10.85
RubberWhale
584x388
0.74
0.29
0.08
14.41
15.63
Grove2
640x480
1.00
0.40
0.10
22.49
24.14
表1 软件执行算法的时间
三、并行性分析
在分析了各个模块及整个光流算法的软件执行时间,有必要从任务并行、数据并行和流水线并行给出它们的并行性分析,进行软硬件协同划分。3.1 任务并行
任务并行就是把处理数据粗粒度地划分为各个模块,每一个模块的相应数据都能够独立处理。在理想状况下,在有足够硬件资源的情况下,并行化的HS工作流程如图3所示。
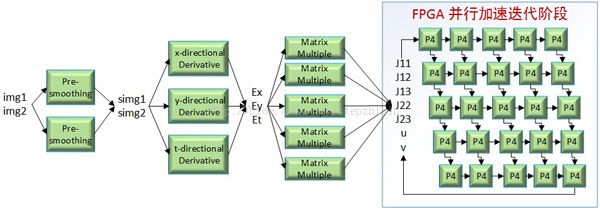
图3 任务并行化的HS光流计算
具体地说,两张要处理的图片(img1和img2)经过两个并发进行的平滑后得到平滑后的图片(simg1和simg2);然后通过水平、垂直和时间梯度的三个任务的并发计算同时得到Ex、Ey和Et;然后通过五个矩阵乘法器得到模型运动的信息(J11、J12、J13、J22和J23);最后再送给迭代模块。
3.2 数据并行
数据并行就是处理的数据进行细粒度地划分,也就是具体到模块内部。预处理阶段(P1)和梯度计算阶段(P2)通过卷积来运算,运动模型构造阶段(P3)通过简单的矩阵相乘,这三个模块的才做很通用,没有太大的数据相关性,因此特别适合做数据并行。然而,迭代阶段(P5)的数据并行性不是很好,它的数据相关性很大,在硬件设计时,如何消除这一数据相关性是关键。
3.3 流水线并行
流水线并行特别适合FPGA处理,在HS光流算法中,如何衔接各个模型间的计算节点,特别是迭代部分的结算节点成了制约流水线关键的一个因素。

图4 光流场计算的模块间的流水线
如图4所示,P4模块需要迭代100次,然而前面的P1、P2、P3模块处理完成的数据如果P4来不及处理的哇,就会造成大量的数据丢失,因此需要存到外部空间,才能让数据不会丢失,这就制约了流水线的性能,是整个流水系统陷入了恶性循环中。
四、基于Zynq的系统设计
在分析了算法的并行性后,下面将从硬件设计、软件设计与系统的优化等角度来说明如何在Zedboard上实现与优化复杂的图像算法的加速机制。
4.1 流水线设计
根据上一章的流水线并行性的分析,可以知道迭代模块是破坏流水性能下降的一个关键点,降低或者消除它的影响成为一个关键点。从流水线的角度,可以通过拉长流水线的级数,来增加流水线的性能;也就是在迭代内部,使用多份P4模块来缓冲从P3级进来的数据,减少了外部迭代的次数,如图5所示。

图5 流水线的优化1
从通信量的角度,光流场的计算需要迭代,需要高速并行访问存储器的结构,因此,数据位宽的大小对通信量有很大的影响。比如迭代的起始点放在P4上,需要256-bit的数据位宽即(J11, J12, J13, J22, J23, u, v),这样会对存储器的读写速率有很高的要求,然而一旦存储器达不到,也同样会堵塞数据流的操作。因此,选择合适的迭代起始点也是一个很重要的因素。如图6所示,如果把迭代的起始点放在P1模块,只需要128-bit的数据位宽即(img1,img2,u, v),相比较图5的流水线结构,它的通信量会下降一半。

图6 流水线的优化2
4.2 迭代系统的设计
在优化完算法的流水线后,流水线与存储器的接口需要进一步优化。在Zedboard的PL端FPGA与DDR的通信方式是基于AXI总线协议的,PL端通用AXI VDMA来读写DDR的数据,具体的硬件结构图如图7表示。
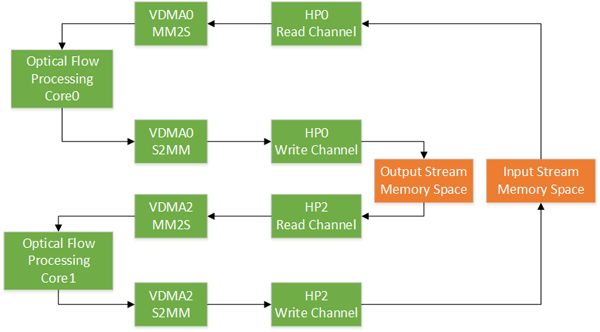
图7 迭代系统的硬件结构图
数据流从HP0口通过VDMA0的MM2S端流到光流算法的IP核,经过流水线处理后写到VDMA0的S2MM端,从VDMA0的S2MM端把数据流写到输出数据区;接着VDMA1的MM2S从HP2口读更新好的值,送给光流算法的IP核处理,处理完的数据由VDMA1的S2MM写入输入数据区;这样流水线的输入输出数据才能与DDR高效地流起来。
4.3 光流算法IP核的设计
根据第三章的并行性分析可知,在光流场计算的内部,迭代阶段的并行性不是很好,具体地表现为每产生一个像素点的光流新值都会去更新,也就是一个像素点与之相邻的上下左右四个像素点的光流值有数据依赖性,因此,消除数据相关性会大大地提高算法的并行性。在设计FPGA的IP核时,采用改进的奇偶超松弛迭代法,能够有效地消除光流的数据相关性。如图8所示,红颜色表示奇数层的迭代,等奇数层的迭代完成之后偶数层再迭代,这样大大提高了算法的并行性。
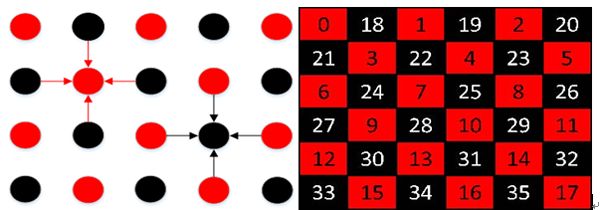
图8 奇偶机制的数据相关性
光流算法的IP核是使用Xilinx的高层综合语言(HLS)来实现的,它能快速地把C、C++和SystemC三种高层次的软件语言转化为VHDL或者Verilog的硬件描述语言。
图8显示了简单的综合流程,从C/C++/SystemC设计开始。C/C++/SystemC 测试平台用于验证设计功能的正确性,同时还可用于RTL和C的协同仿真。协同仿真包括验证生成的RTL设计(.v或.vhd)功能,这要使用C/C++/SystemC测试平台而不是RTL测试平台或者采用e或Vera验证语言编写的测试平台。时钟周期约束设置了设计应该运行的目标时钟周期。设计将被映射到目标FPGA器件——Xilinx FPGA上,如图9所示。
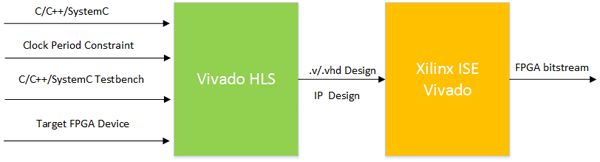
图9 采用Vivado HLS进行FPGA综合的流程
对于Vivado HLS中的许多高级特性而言,需要了解什么样的硬件架构,从而进行源代码的调整, 具体地开发手册可以参考[26]。为了适应不同图片的大小,增强IP核的通用性,综合硬件资源等方面的考虑,调用IP核中图片宽度最大支持到640,具体的光流算法的HLS设计可以参考我们的源代码。
4.4 FPGA的资源利用率
表2是在Zedboard下FPGA的资源利用率,其中光流计算的IP核中P5的硬件结构是2份,数据通路的工作频率是100MHZ,控制通路的工作频率是50MHZ。从表中可以看出,FPGA的资源已经消耗了一大半,如果在硬件资源足够的情况下,可以把P5做成更多的份数,这样可以减少外部迭代的次数,从而提高整个系统的吞吐率。
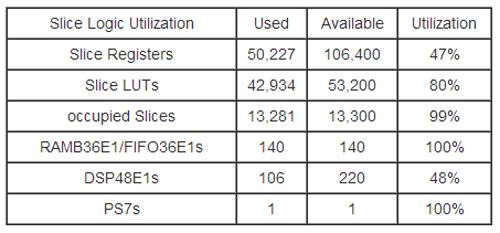
表2 FPGA的资源利用率
4.5 软硬件协同设计
在硬件结构的设计中,模块中需要软件去控制或者配置FPGA的IP核,这些信号线通过AXI4-lite总线映射到内存区域,也就是地址线。这样就使得硬件的可扩展性大大地增强。光流算法的IP核的地址控制信号如表3所示,通过地址信号线的寄存器的设置对FPGA的IP核进行软件配置、复位、启动。VDMA的IP核的控制可以参考[27] 。
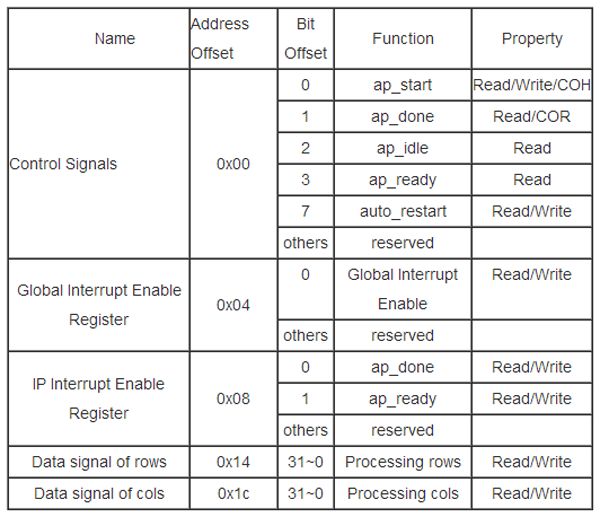
表3 光流计算的IP核的软件控制
Note: SC = Self Clear, COR = Clear on Read, TOW = Toggle on Write,
COH = Clear on Handshake
五、实验
5.1 迭代对时间的影响
不同的迭代次数对算法的执行效率有很大的影响,如图10所示, HSW表示软硬件协同的执行时间,对应于左边的时间标注; SW表示软件的执行时间,对应于右边的时间标注;测试图片大小为640x480。随着迭代次数的增加,不管是软件还是软硬件协同,系统的执行时间都会有相应的增长;但是软件的执行时间随着迭代次数的增加,上升的幅度比软硬件的执行时间要大得多。然而软硬件协同工作的方式的执行时间在同样的迭代次数下比纯软件操作要快35倍。
图10 迭代次数对执行时间的影响
5.2 不同图片大小对时间的影响
在通用CPU的环境中,如纯ARM处理器下,随着图片的不断增大,算法的执行效率会直线下降;在软硬件协同的情况下,FPGA对核心算法的进行加速运算,软件对FPGA内部的IP核进行控制,以及加载初始化数据与保存最种结果。从表4下可以看出,随着图片的变大,FPGA处理的部分增长的很小,ARM外围控制的时间显得就突出出来;但是软硬件协同执行的时间平均要比软件的执行时间快25倍左右,特别是对于大的图片,比如640x480的分辨率,软硬件协同的执行时间比纯软件执行要快35倍。对于光流算法,分辨率越大,计算出来的光流的细粒度也就越好,效果也就越准确。
Image
Size
SW Time [s]
HSW Time [s]
HW
SW
Real Time
Yosemite
316x252
4.84
0.26
0.12
0.38
Venus
420x380
10.99
0.26
0.23
0.49
RubberWhale
584x388
15.16
0.28
0.33
0.61
Grove2
640x480
24.18
0.29
0.42
0.71
表4 不同图片大小对时间的影响
5.3 软件和软硬件协同工作效果的比较
软件与软硬件协同工作的光流场计算效果如图11所示,实验效果表明,在同样的配置参数下,软硬件协同计算光流的效果与软件计算的光溜效果相差不大。在Yosemite图片中,底部出现了一些瑕疵点,原因是计算光流的IP核里面的一些数据还停留在流水线里,需要再添加几行的数据将其顶出来。
图11 软件与硬件效果图比较
六、实验
参考文献
[1] http://en.wikipedia.org/wiki/Optical_flow.
[2] Bruce D. Lucas and Takeo Kanade, An iterative image registration technique with an application to stereo vision, Proceedings of Imaging Understanding Workshop, 1981, pp. 121-130.
[3] Jianbo Shi and Carlo Tomasi, Good features to track, IEEE Conference on Computer Vision and Pattern Recognition, (CVPR 1994), pp. 593-600.
[4] M. P. Sudipta, N. Sinha, Jan-Michael Frahm and Y. Genc, Feature tracking and matching in video using programmable graphics hardware, Machine Vision and Applications, 2007, vol. 30, pp. 185-198.
[5] Berthold K.P. Horn and Brian G. Schunck, Determining optical flow, Artificial Intelligence (AI 1981), Volume 17, Issues 1-3, pp. 185-203.
[6] T. Brox, A. Bruhn, N. Papenberg, and J. Weickert, High accuracy optical flow estimation based on a theory for warping, 8th European Conference on Computer Vision (ECCV 2004), pp. 25-36.
[7] A. Bruhn, J. Weickert, and C. Schnorr, Lucas/kanade meets horn/schunck: Combining local and global optic flow methods, International Journal of Computer Vision (IJCV 2005), 61:3, pp. 211–231.
[8] J.L. Barron, D.J. Fleet, S.S. Beauchemin, Performance of optical flow Techniques, International Journal of Computer Vision (IJCV 1994), 12:1, pp.43-77.
[9] S. Baker, D. Scharstein, J. Lewis, S. Roth, M. J. Black, and R. Szeliski, A database and evaluation methodology for optical flow. International Journal of Computer Vision (IJCV 2011) 92, 1–31.
[10] G. Farneback. Very high accuracy velocity estimation using orientation tensors, parametric motion, and simultaneous segmentation of the motion field. In Proc. Eighth International Conference on Computer Vision (ICCV 2001), volume 1, pp.171–177.
[11] J. Wills, S. Agarwal, and S. Belongie. A feature-based approach for dense segmentation and estimation of large disparity motion. International Journal of Computer Vision (IJCV 2006), 68:2, pp.125–143.
[12] Anandan P, A computational framework and an algorithm for the measurement of visual motion, International Journal of Computer Vision (IJCV 1989) 2, pp. 283-310.
[13] Heeger D.J, Optical flow using spatiotemporal filters, International Journal of Computer Vision (IJCV 1990) 1, pp. 279-302.
[14] Fleet D.J. and Jepson A.D, Computation of component image velocity from local phase information, International Journal of Computer Vision (IJCV 1990), Vision 5, pp. 77-104.
[15] J. Weickert and C. Schnorr,CHNORR, A theoretical framework for convex regularizers in pde-based computation of image motion. International Journal of Computer Vision (IJCV 2001), 45: 3, pp. 245–264.
[16] Thomas Brox, Jitendra Malik, large displacement optical flow: descriptor matching in variational motion estimation, IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI 2011), pp. 500 - 513.
[17] M. J. Black and P. Anandan, The robust estimation of multiple motions: Parametric and piecewise smooth flow fields, Computer Vision and Image Understanding (CVIU 1996), 63:1, pp. 45–104.
[18] A. Bruhn and J. Weickert, A multigrid platform for real-time motion computation with discontinuity-preserving variational methods, International Journal of Computer Vision(IJCV 2006), 70, pp. 257–277.
[19] P. Gwosdek, A. Bruhn, and J. Weickert, Variational optic flow on the sony playstation 3. Real Time Image Proc ( RTIP 2010), 5.
[20] H. Grossauer and P. Thoman, Gpu-based multi-grid:real-time performance in high resolution nonlinear image processing. International Conference on Computer Vision System (ICVS 2008), pp.141–150.
[21] Zhilei Chai, Jianbo Shi, Improving KLT in embedded systems by processing oversampling video sequence in real-time, 5th International Conference on Reconfigurable Computing and FPGAs (Reconfig2011), pp. 297-302.
[22] J. L. Martin, A. Zuloaga, C. Cuadrado, J. Lazaro and U. Bidarte, Hardware implementation of optical flow constraint equation using FPGAs, Computer Vision and Image Understanding (CVIU 2005), pp. 462-490.
[23] R. Rustam, N. H. Hamid and F. A. Hussin, FPGA-based Hardware Implementation of Optical Flow Constraint Equation of Horn and Schunck, 2012 4th International Conference on Intelligent and Advanced Systems (ICIAS2012), pp. 790-794.
[24] E. S. Chung, P. A. Milder, J. C. Hoe, and K. Mai, “Single-Chip Hetero-
geneous Computing:Does the Future Include Custom Logic, FPGAs, and
GPGPUs,” in Proc. 43rd Annual IEEE/ACM International Symposium on
Microarchitecture, Atlanta, GA, Dec 4-8, 2010.
[25] Xilinx. [Online]. Available: http://www.xilinx.com/products/silicon-devices/soc/zynq-7000/index.htm