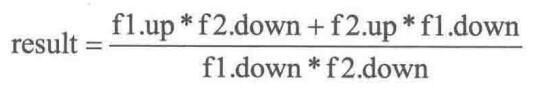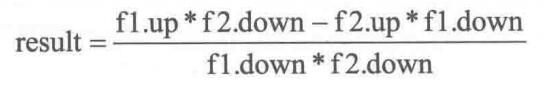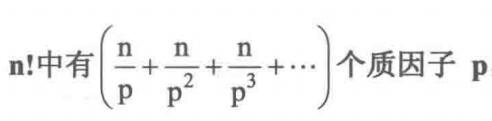PAT-考前总结
PAT 考前总结
1. C/C++ 基础
1. 1 类型
1.2 输入输出
1.2.1 scanf与cin的速度以及解决方案
scanf在输入上比cin要快,如果非要用cin,又要追求速度,可以使用
ios::sync_with_stdio(false);
使用C风格输入字符串不太用好,而cin输入输出字符串是很方便的。如果使用cin输入的字符串必须要使用scanf输出的话,可以使用c_str()函数,如:
#include
#include
string s;
cin >> s;
printf("%s", s.c_str());
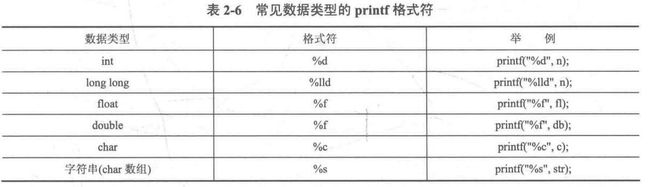
1.2.2 scanf与printf的格式
1.2.3 自定义输入输出流
在C下,可以使用sscanf()函数,如:
string s = "1 3";
int a, b;
sscanf(s, "%d%d", &a, &b); // a = 1, b = 3
在C++下,需要使用stringstream:
#include
stringstream ss;
ss.str("a 4");
char c;
int a;
ss >> c >> a;
// 注意
ss << "abc";
// 不是将abc给ss,而要使用
ss.str("内容");
1.3 使用STL
使用STL时,不要忘记:
using namespace std;
PS: 关于STL的详细使用见后面章节
1.4 一些常用函数
1.4.1 字符类型检查
在
1. `isalnum()`是字母或数字。
2. `isalpha()`是字母。
3. `isdigit()`是数字。
4. `isupper()`是大写字母。
5. `islower()`是小写字母。
6. `isblank()`是空格/tab键。
7. `isspace()`是空格/tab/回车。
1.4.2 字符串与整形的转换
1.4.2.1 stoi()函数
stoi接受string作为参数,数字范围int,溢出报错。
1.4.2.2 atoi()函数
atoi接受char*作为参数,数字范围int溢出只输出上/下界。
1.4.3 二分查找函数
二分查找的函数有 3 个: 参考:C++ lower_bound 和upper_bound
lower_bound(起始地址,结束地址,要查找的数值) 返回的是数值 第一个 出现的位置。
upper_bound(起始地址,结束地址,要查找的数值) 返回的是数值 最后一个 出现的位置。
binary_search(起始地址,结束地址,要查找的数值) 返回的是是否存在这么一个数,是一个bool值。
1.4.4 fill()与memset()
fill()的用法:
fill(vec.begin(), vec.end(), val);
其中val为要赋的值。
memset()的用法:
const int INF = 0x3f3f3f3f;
int a[1000];
memset(a, INF, sizeof(a));
注:memset()只推荐赋值0,1,inf。
(其中inf一般设为0x3f)
2. 基础算法
2.1 二分查找
在一个严格递增的序列A中找出给定的数x。
时间复杂度: O(logn)。
// 在数组A的[left, right]区间中二分查找x
int binarySearch (int A[], int left, int right, int x) {
int mid;
while(left <= right) {
mid = (left+right)/2;
if (A[mid] == x) {
return mid;
} else if (A[mid] < x) {
left = mid+1; // x在右子区间[mid+1, right]中
} else {
right = mid-1; // x在左子区间[left, mid-1]中
}
}
return -1; // 查找失败
}
2.2 快速排序
划分元素:
// 对区间[left, right]的元素进行划分,返回base
int Partition(int A[], int left, int right) {
int temp = A[left]; // 先保存好base
while(left < right) {
while(left < right && A[right] > temp) right--;
A[left] = A[right];
while(left < right && A[left] <= temp) left++;
A[right] = A[left];
}
A[left] = temp;
return left; // 返回相遇的下标
}
快排:
// 对数组A[]中[left, right]中的元素快速排序
void quickSort(int A[], int left, int right) {
if (left < right) {
// 将A按A[left]划分
int pos = Partition(A, left, right);
quickSort(A, left, pos-1); // 对左子区间快排
quickSort(A, pos+1, right); // 对右子区间快排
}
}
3. 数学问题
3.1 最大公约数与最小公倍数
3.1.1 最大公约数 gcd(a, b)
// 求解a与b的最大公约数
int gcd(int a, int b) {
if (b == 0) return a;
return gcd(b, a%b);
}
3.1.2 最小公倍数 lcm(a, b)
最小公倍数与最大公约数的关系如下:
若
gcd(a, b) = c,则lcm(a, b) = (a*b)/c。但由于a·b可能会溢出,所以采用a/c·b。
// 求解a与b的最小公倍数
int lcm(int a, int b) {
int c = gcd(a, b);
return a/c*b;
}
3.2 分数的表示与化简
3.2.1 分数的表示
存储为假分数,但约定:
1. 分母为非负数。
2. 若分数为0,则分子为0,分母为1。
3. 分子和分母没有除1之外的公约数。
定义:
struct Fraction {
int up, down;
};
3.2.2 分数的化简
分为三步:
1. 若分母为负数,将分子分母都变为相反数。
2. 若分子为0,将分母设为1。
3. 求出分子分母的最大公约数g,分子分母同除g。
代码:
// 对分数f进行约分
Fraction reduction(Fraction f) {
if (f.down < 0) {
f.down = -1*f.down;
f.up = -1*f.up;
}
if (f.up == 0) f.down = 1;
else {
int g = gcd(abs(f.up), abs(f.down));
f.up /= g;
f.down /= g;
}
return f
}
3.2.4 分数的四则运算
3.2.4.1 加法
计算公式:
代码:
// 分数a与b相加
Fraction add(Fraction a, Fraction b) {
Fraction res;
res.up = a.up*b.down + b.up*a.down;
res.down = a.down*b.down;
return reduction(res); // 返回约分后的
}
3.2.4.2 减法
计算公式:
代码:
// 分数a减去b
Fraction minu(Fraction a, Fraction b) {
Fraction res;
res.up = a.up*b.down - b.up*a.down;
res.down = a.down*b.down;
return reduction(res);
}
3.2.4.3 乘法
计算公式:
代码:
// 分数a乘以b
Fraction multi(Fraction a, Fraction b) {
Fraction res;
res.up = a.up*b.up;
res.down = a.down*b.down;
return reduction(res);
}
3.2.4.4 除法
计算公式:
代码:
// 分数a除以b
Fraction dicide(Fraction a, Fraction b) {
Fraction res;
res.up = a.up*b.down;
res.down = a.down*b.up;
return reduction(res);
}
3.2.4 分数的输出
1. 化简
2. 若分母为1,分数为整数,只输出整数。
3. 若分子绝对值大于分母,应输出带分数。
4. 1-3均不满足,按照真分数输出即可。
代码:
// 输出分数
void showFraction(Fraction a) {
a = reduction(a);
if(a.down == 1) {
// 整数
printf("%d", a.up);
} else if {
// 带分数
printf("%d %d/%d", a.up/a.down, abs(a.up)%a.down, a.down);
} else {
// 真分数
printf("%d/%d", a.up, a.down);
}
}
3.3 素数
3.3.1 素数的判断
// 判断n是否为素数
bool isPrime(int n) {
if (n <= 1) return false; // 特判,人为规定
int sqr = sqrt(1.0*n);
for(int i = 2; i < sqr; i++) {
if (n%i == 0) return false; // n不为素数
}
return true;
}
3.3.2 素数表的获取
代码如下:
const int maxn = 1000; // 表长
int prime[maxn], pNum = 0; // 存放所有素数的表,与素数个数
int p[maxn] = {0}; // p[i] 为素数,则p[i] = false
void getPrime() {
for(int i = 2; i < maxn; i++) {
if (p[i] == false) {
// i是素数,筛去i的倍数
for(int j = i+i; j < maxn; j += i) {
p[j] = true;
}
}
}
}
复杂度为:O(nloglogn)。
3.3.3 质因子分解
先定义一个存放质因子的结构体:
struct Factor{
int x, cnt; // x为质因子,cnt为其个数
};
下面的代码将数字n质因数分解,返回分解结果:
// 质因数分解
Factor res[10]; // 对于int类型的n,开十位够了。
Factor factorization(int n) {
int sqr = sqrt(n), num = 0;
// 遍历小于sqr的质因子,判断是否为n的因子
for(int i = 0; i < sqr; i++) {
if (n % prime[i] == 0) {
res[num].x = prime[i];
res[num].cnt = 0;
while(n%prime[i] == 0) {
res[num].cnt=+;
n /= prime[i];
}
}
num++;
}
if (n != 1) {
fac[num].x = n;
fac[num++].cnt = 1;
}
}
3.4 大整数运算
3.4.1 大整数的存储
使用数组(int型与string型皆可),整数的高位存在数组的高位,整数的地位存在数组的低位(这种情况下输入为字符串的数字要先反转一下)。
定义:
struct bign {
int d[1000];
int len;
bign() {
memset(d, 0, sizeof(d));
}
};
字符串到大整数的转换:
逆着赋值即可。
大整数的比较,类似于字符串的比较。
3.4.2 大整数的运算
3.4.2.1 高精度加
模拟竖式计算加法,按位相加并加上进位即可。
实现:
// 大整数a与b相加,返回结果
bign add(bign a, bign b) {
bign res;
int carry = 0;
for(int i = 0; i < a.len || i < b.len; i++) {
int temp = a.d[i] + b.d[i] + carry; // 对应位数相加,再加上进位
res.d[res.len++] = temp%10; // 个位数为该位结果
carry = temp/10; // 十位数为进位
}
if (carry != 0) { // 若还有进位,赋给最高位
res.d[res.len++] = carry;
}
return res;
}
3.4.2.2 高精度减
同样模拟竖式计算即可。但在开始相减之前,确保被减数大于减数,若小于先标记负号,再用减数减去被减数。
具体步骤为:从各位开始每位相减,先比较被减位与减位的大小,若被减位较小,将高位减一,被减位加十再相减。最后高位可能会有多余的零,需要重新调整len。
实现:
// 大整数a与b相减,返回结果
bign sub(bign a, bign b) {
bign res;
for(int i = 0; i < a.len || i < b.len; i++) {
if (a.d[i] < b.d[i]) {
a.d[i+1]--;
a.d[i] += 10;
}
res.d[res.len++] = a.d[i] - b.d[i];
}
while(res.d[res.len] == 0 && res.len >= 2) {
res.len++;
}
return res;
}
高精与低精的乘除这里忽略。
3.5 拓展欧几里得算法
拓展欧几里得定义为:给定两个非零整数a、b,求一组整数解(x,y),使得ax+by = gcd(a, b)。
求解如下:
// 求解拓展欧几里得,并返回gcd(a, b)
int exGcd(int a, int b, int &x, int &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
int g = exGcd(b, a%b, x, y);
int temp = x;
x = y;
y = temp - a/b*y;
return g;
}
3.6 组合数
3.6.1 关于n!的一个问题
求n!中有多少个质因子p?
答案是:
代码实现:
// 计算n!中有多少个质因子p
int cal(int n, int p) {
int res = 0;
while(n) {
res += n/p;
n/=p;
}
return res;
}
3.6.2 组合数的计算
组合数的定义式为:
若直接通过定义式计算,即使使用long long类型也只能接受n <= 20的数。
方法二:通过递推公式计算。递推公式是指:从n个数中选出m个数,可以分为两种方案之和:
1. 最后一个数不选,那么为从n-1个数中选m个数。
2. 最后一个数选择,那么为从n-1个数中选m-1个数。
即:
第一直觉就是使用递推计算,但参考斐波那契,应该记录计算结果防止重复计算。
实现:
long long res[67][67] = {0};
long long cal(long long n, long long m) {
if (m == n || m == 0) return 1;
if (res[n][m] != 0) return res[n][m];
return res[n][m] = cal(n-1, m) + cal(n-1, m-1); // 赋值并返回
}
4. STL
注:STL各种容器的使用均需要
using namespace std;
4.1 vector-向量
4.1.1 定义
vector name; // 一维
vector< vector > name; // 二维
注意在写二维时,两个尖括号需要有空格,否则在某些编译器下会将其当作位运算操作符。
4.1.2 访问
vector即可用下标访问,也可用迭代器访问。迭代器的定义如下:
vector::iterator it;
4.1.3 常用特殊操作
一些push_back()的函数就不在这里赘述了。写一些常用的操作:
-
合并/拼接两个vector
vec1.insert(vec1.end(), vec2.begin(), vec2.end()); -
删除一个元素
使用
erase(it)可以删除迭代器it处的数据,注意其返回值为被删除元素向后的下一个元素。也可以删除一个范围内的元素:
vec.erase(vec.begin()+3, vec.begin()+6);将会删除第三个位置到第6个位置的元素(左闭右开)。
4.1.4 左闭右开
vec.begin()是第一个元素,但vec.end()是最后一个元素之后的指针。
所以[vec.begin(), ve.end()]其实是左闭右开区间。
在某些函数传范围时大多也是左闭右开区间。
4.2 set-集合
set是一个内部有序且不含重复元素的容器。
4.2.1 定义
定义set,与vector类似,但set只能通过迭代器访问。
注:只有vector与string能通过下标访问。
4.2.2 常用函数
find(val)返回对应值为val的迭代器,若没找到将会返回s.end()。
4.3 string-串
要读入与输出整个字符串,只能用cin与cout。(也可用c_str()使用C风格输出)
4.3.1 常用函数
str1.find(str2)当str2是str1的字串时,返回str2第一次出现的位置,若不是返回string::npos。
if (str1.find(str2) != string::npos) {
// 找到str2
}
str1.replace(pos, len, str2)将str1从pos开始,长度为len的字串替换为str2。
4.4 map-映射
map可以将任何基本类型映射到任何基本类型。键与值也是唯一的。
4.4.1 定义
map mp; // 定义了int到string的映射。
4.4.2 访问
只能通过迭代器访问,对于迭代器it:
it->first; // 键
it->second; // 值
4.4.3 常用函数
find(key)函数返回键为key的迭代器,若没有返回end()。
删除可以通过迭代器或键值删除:erase(it) 或 erase(key),也可以传入区间删除。
此外,C++11标准中增加了unordered_map,使其不按key排序。
4.5 queue-队列
访问使用front()与back(),入队与出队使用push(val)与pop(),判空使用empty()。
4.5.1 优先队列
队首元素一定是当前队列中优先级最高的那一个。
4.5.1.1 访问
只能使用top()访问队首元素。
4.5.1.2 设置优先级
对于基本类型,优先队列默认是数字大的优先级越高。下面的两种定义是等价的:
priority_queue q;
priority_queue< int, vector, less > q;
其中参数vector是承载底层数据结构的容器,less是第一个参数的比较类表示数字大的优先级大,若要设置为数字小的优先级小,使用greater。
对于其他的数据结构,需要重载<。如,对下面的水果类设置价格高的优先级高:
struct fruit {
string name;
int price;
// 重载 <
friend bool operator < (fruit a, fruit b) {
return a.price < b.price;
}
};
注:只能重载小于号,不能重载大于号。
4.6 stack-栈
后进先出,与队列的访问区别在于栈顶使用top()函数获取。
4.6.1 出入栈序列合法性判定
对于给定入栈序列:1,2,3…
判断出栈序列是否合法。
// 判断入栈序列为a[]的情况下,出栈序列b[]是否合法
bool check(vector a, vector b) {
int index = 0;// 记录出栈
stack s;
for(int i = 0; i < a.size(); i++) {
s.push(a[i]);
while(!s.empty() && s.top() == b[index]) {
index++;
s.pop();
}
}
return s.size() == 0 ? true:false;
}
4.6.2 queue与stack的应用-中后缀表达式的转换与计算
对于中缀表达式a + b,其后缀表达式为a b +。当中缀表达式比较复杂时,要计算表达式的值,需要转化为后置表达式进行计算。
首先定义每个元素:
struct node {
double num;
char op;
bool flag; // true表示操作数,false表示操作符
};
将前缀表达式转为中缀表达式的步骤如下:
1. 将前缀表达式按照string读入,删除空格。从前至后遍历。
2. 定义两个栈q与s,分别存储后缀表达式与临时操作符。
3. 当遇到操作数时压入q。
4. 当遇到操作符时,比较s栈顶的操作符与当前操作符的优先级(乘除>加减)。
5. 若s栈顶操作符优先级高,就将其压入后缀表达式中。直到当前操作符高于栈顶操作符为止。
6. 若最后s中还有操作符,一一压入q中。
实现:
map op; // op['*'] = op['/'] = 2;op['+'] = op['-'] = 1
// 将string转化为后缀表达式
queue change(string str) {
for(string::iterator it = str.begin(); it != str.end(); it++) {
if (*it == ' ') str.erase(it);
}
node tmp;
stack s;
queue q;
for(int i = 0; i < str.size();) {
if (isdigit(str[i])) {
// 操作数
tmp.flag = true;
tmp.num = str[i++] - '0';
while(i < str.size() && isdigit(str[i])) {
tmp.num = tmp.num*10 + (str[i] - '0');
i++;
}
q.push(tmp);
} else {
// 操作符
tmp.flag = false;
tmp.op = str[i];
while(!s.empty() && op[str[i]] <= op[s.top().op]) {
q.push(s.top());
s.pop();
}
s.push(tmp);
i++;
}
}
while(!s.empty()) {
q.push(s.top());
s.pop();
}
return q;
}
计算后缀表达式的值的步骤如下:
1. 从q中依次出栈,临时放入栈s
2. 若当前出栈为操作数,直接压入s
3. 若当前出栈为操作符,从s中弹出两个操作数,做当前操作符的运算,将运算结果压入s
4. 最后s中只有一个数字,就是表达式的值
实现如下:
double cal(queue q) {
stack s;
node tmp;
double num1, num2;
while(!q.empty()) {
tmp = q.front();
q.pop();
if (tmp.flag) {
// 操作数
s.push(tmp.num);
} else {
// 操作符
num2 = s.top(); // 注意这里先读入的是第一个操作符
s.pop();
num1 = s.top();
s.pop();
if (tmp.op == '+') num1 = num1 + num2;
else if (tmp.op == '-') num1 = num1 - num2;
else if (tmp.op == '*') num1 = num1 * num2;
else num1 = num1 / num2;
s.push(num1);
}
}
return s.top();
}
练习:Codeup-1918-简单计算器
4.7 pair-对
pair可以定义一对元素。其定义于头文件
用法:
pair p;
make_prie(1, "hello");
p->first; // 第一个元素 1
p->second; // 第二个元素 hello
4.8 定义在algorithm下的常用函数
4.8.1 max(),min(),abs()
用法如下:
max(a, b)返回a与b中的最大值,反之min(a, b)返回最小值。
abs(x)返回x的绝对值,x必须为整数。浮点型的绝对值用math头文件下的fabs。
4.8.2 swap()
swap(x, y)交换x与y的值。
4.8.3 reverse()
reverse(it1, it2)可以将指针在[it1, it2)之间的元素反转。
4.8.4 next_permutation()
给出一个序列在全排列中的下一个排列。
示例:
#include
#include
using namespace std;
int main () {
int a[10] = {1, 2, 3};
// 求a[0]-a[2]之间元素的全排列
do {
printf("%d %d %d\n", a[0], a[1], a[2]);
} while(next_permutation(a, a+3));
}
4.8.5 fill()
见1.4.4。
4.8.6 sort()
排序函数,默认升序排序。
基本用法
vector v;
// 初始化v = {5, 6, 8, 2, 3, 9, 0}
sort(v.begin(), v.end());
// v = {0,2,3,5,6,8,9}
或用于数组
sort(a, a+5),将会对数组a的前5个数进行升序排序。
也可以自定义比较函数:
示例:
struct fruit{
string name;
int price;
};
vector f;
// 初始化一堆fruit到f中,现在想要按照价格降序排列,可以自定义cmp函数
bool cmp(fruit a, fruit b) {
return a.price > b.price;
}
sort(f.begin(), f.end(), cmp);
当排序要求有类似
优先按照x升序排列,若x相同,按照y降序排列时,可以在cmp函数中处理。逻辑一般为:
bool cmp (Type a,Type b) { if (a.x != b.x) return a.x < b.x; return a.y > b.y; }
4.8.7 lower_bound()与upper_bound()
二分查找函数,需要用在一个有序数组中。说明见1.4.3,下面是对数组与向量的用法:
lower_bound(a, a+10, val); // 数组
lower_bound(v.begin(), v.end(), val); // 向量
5. 高级算法与数据结构
5.1 链表
这里不赘述一些概念以及链表定义创建等操作,只介绍一些常用或实用的方法思路。
5.1.1 重建链/去除非链节点
在PAT以及其他OJ题目中,常会给你一些离散的节点与头节点,说这是一个链表,但不排除其中有非该链上的节点。这种时候我们需要先将这些节点先输入保存到vector中,然后再从头元素开始遍历链,将完整的链建立起来,去除非链节点。方法很简单,从头元素开始,一直向下一个元素找去,直到指向下一个元素的指针为空即可,将所有元素压入vector。
一般节点是给出地址,数据,下一个的地址。我们使用数组,将在地址为a的元素保存在数组下标为a处即可。
设节点为:
// 输入节点
struct node {
int add; // 地址
int data; // 保存的数据
int next; // 用int指向下一个节点在数组中的下标
};
假设输入为:
int head; // 头节点的下标(即头节点地址)
vector seq; // 给出的所有节点
vector list; // 实际的所有链上元素
重建链:
node p = seq[head];
while (p) {
list.push_back(p);
p = seq[p.next];
}
5.1.2 链表逆序
一般例如二分,逆序,删除,排序等函数如果在可以使用STl中的方法实现的情况下,不推荐自己写这样的函数实现,因为这样可能会提高代码复杂度与出错率。
对于链表的逆序,可以直接调用reverse(vec.begin(), vec.end());完成,当然区间也可以自己定义。
对于一定要自定义链表逆序的情况不太常见,这里只给出逆序步骤。(懒得写实现了)
下面为对头节点为h的链表,整个逆序的步骤:
1. 重新定义一个节点head作为新链的头节点,定义p指向新链的最后一个元素。
2. 对原链表遍历,对于每个节点n每次做以下操作:
- 保存节点n的父亲节点,将n的父亲节点的后继设置为n的后继。这样就将节点n从原链中拿出来了。
- 之后将节点n链到新节点最后面,即`p->next = n`。
3. 新链即为逆序后的链
5.2 BFS/DFS-深搜与广搜
深搜与广搜都是对于路径来说的,但并不局限于图这种明显是路径的数据结构,对于很多查找/搜索的问题,都可以用它们解决,因为查找本身就可以抽象为树或图。在写树、图等高级数据结构之前,先介绍这两种搜索方式。
下列实现均使用图完成,其他情况可以理解该搜索方式后自行实现。
5.2.1 DFS-深度优先搜索
5.2.1.1 定义
通俗来说就是每次遇到岔路都走进去,一条道走到黑,直到没路可走了才回到岔路口,再进入零一条岔路。对于所有岔路都如此处理。
5.2.1.2 实现
借助栈。这里使用邻接链表保存图,对于图的保存方式,可以查看 图。
// 遍历邻接链表mp表示的图,起点为s
void dfs(vector< vector >mp, int start) {
stack s;
s.push(start);
int temp;
while(!s.empty()) {
temp = s.top();
s.pop();
for(int i = 0; i < mp[temp].size(); i++) {
s.push(mp[temp][i]);
}
// 访问temp
}
}
5.2.2 BFS-广度优先搜索
5.2.2.1 定义
每到一个岔路口,先逐个进入岔路口看看这个岔路下还有哪些岔路,再回来尝试下一个岔路。
5.2.2.2 实现
实现借助队列。仍然使用邻接链表保存图。
// 从点start开始,广度优先遍历邻接链表保存的图mp
void bfs(vector< vector > mp, int start) {
int temp;
queue q;
q.push(start);
while(!q.empty()) {
temp = q.front();
q.pop();
for(int i = 0; i < mp[temp].size(); i++) {
q.push(mp[temp][i]);
}
// 访问temp
}
}
5.3 树与二叉树
5.3.1 二叉树
定义:
1. 要么二叉树没有根节点,是一颗空树。
2. 要么二叉树由根节点、左子树、右子树组成,且左右子树各是二叉树。
定义实现:
struct node {
int data; // 数据域
node *lchild; // 左子树
node *rchild; // 右子树
};
5.3.1.1 二叉树的遍历
先序遍历:
// 先序遍历二叉树
void preorder (node *root) {
if (!root) return; // 空树
printf("%d/n", root->data); // 访问该节点
preorder(root->lchild); // 访问左子树
preorder(root->rchild); // 访问右子树
}
中序遍历:
// 中序遍历二叉树
void inorder (node *root) {
if (!root) return; // 空树
preorder(root->lchild); // 访问左子树
printf("%d/n", root->data); // 访问该节点
preorder(root->rchild); // 访问右子树
}
后序遍历:
// 后序遍历二叉树
void postorder (node *root) {
if (!root) return; // 空树
preorder(root->lchild); // 访问左子树
preorder(root->rchild); // 访问右子树
printf("%d/n", root->data); // 访问该节点
}
可以看出,在递归遍历二叉树中先中后序只是访问节点的位置不同。
二叉树的层序遍历,即从根节点开始的bfs。
5.3.1.2 先中后序重建二叉树
来看这样一个问题:知道二叉树的先序遍历序列与中序遍历序列,能否推出原来的二叉树?
解析:由于先序遍历总是先输出根节点,那么先序遍历的第一个元素就是根节点,而中序遍历中,总是把左子树遍历完再访问根节点,然后再访问右子树。而由于我们从先序遍历中已经知道根节点是谁了,那在中序遍历序列中找到根节点的位置,就知道左子树序列与右子树序列了。这样我们就知道了左子树与右子树的先序与中序序列,然后递归的将左右子树再建立起来就建立起原来的二叉树了。
整个过程的图解可以看我的这篇文章:重建二叉树
实现方式:
vector pre, mid; // 先序与中序序列
int cur = 0;
int getIndex(int n) {
for(int i = 0; i < mid.size(); i++) {
if (mid[i] == n) return i;
}
returen -1;
}
// 使用先序与中序遍历序列重建二叉树,返回二叉树根节点
Node *create(int left, int right) {
if (lect > right) return NULL;
int rt = pre[cur];
int rootIndex = getIndex(rt);
cur++;
node *t = new Node;
t->data = rt;
if (lect != right) {
t->lchild = create(left, rootIndex - 1);
t->rchild = create(rootIndex + 1, right);
}
return t;
}
5.3.2 二叉搜索树
定义:
1. 要么二叉查找树是一颗空树。
2. 要么二叉查找树由根节点,左右子树组成。其中左右子树都是二叉查找树。并且左子树上所有节点都小于等于根节点,右子树上的节点都大于根节点。
5.3.2.1 建立
即将值插入二叉搜索树。
// 将x插入到根节点为root的二叉搜索树中
void insert(node* &root, int x) {
if (!root) {
root = new node;
root->data = x;
return;
}
if (x == root->data) {
// 值已存在,直接返回
return;
} else (x < root->data) { // 插入到左子树
insert(root->lchild, x);
} else { // 插入到右子树
insert(root->rchild, x);
}
}
5.3.2.2 查找
从根节点开始,每个节点与当前值比较,然后确定在左子树还是右子树中查找。
// 在以root为根的二叉搜索树中查找值为x的节点
void search(node *root, int x) {
if (!root) {
// 查找失败
printf("not found!");
return;
}
if (x == root->data) {
// 找到了
printf("found!");
return;
} else if (x < root->data) {
// 在左子树中查找
search(root->lchild, x);
} else {
// 在右子树中查找
search(root->rchild, x);
}
}
5.3.2.5 性质
对二叉搜索树进行中序遍历,结果是有序的。
5.3.2.4 AVL-平衡二叉树 [弃]
平衡二叉树是解决左右子树高度相差太大,导致二叉搜索树的平均查找长度不能达到理论的logn这一问题的方案。其主要思想为,每次元素插入时,总会查看当前二叉树的结构是否平衡(该概念自行了解),若不平衡就旋转调整二叉树,使其平衡。
由于PAT现已不考AVL,故具体实现与细节这里不再赘述。
5.3.3 哈夫曼树
哈夫曼树是解决树的最小带权路径长度的方案。对于一些离散的节点,构建哈夫曼树的思想是:
反复选择两个最小的元素,合并,将其两个合并后的根节点设置为他们权之和;重复选择合并直到只剩下一个元素。
其实现可以借助优先队列,每次弹出两个元素,生成新的根节点再入队,直到只剩下一个元素。
struct node {
int data;
node* lchild;
node* rchild;
friend bool operator < (node a, node b) { // 重载<,使优先队列为小根堆
return a.data > b.data;
}
};
// 由一系列离散的节点构建哈夫曼树
void hafman(vector list) {
priority_queue q; // 定义小顶堆
for (int i = 0; i < list.size(); i++) {
q.push(list[i]);
}
node root,temp, n1, n2;
while (q.size() > 1) {
n1 = q.top();
q.pop();
n2 = q.top();
q.pop();
temp.data = n1.data + n2.data;
temp->left = &(n1);
temp->right = &(n2);
q.push(temp); // 合并后的根节点再压入队列
}
root = q.top();
}
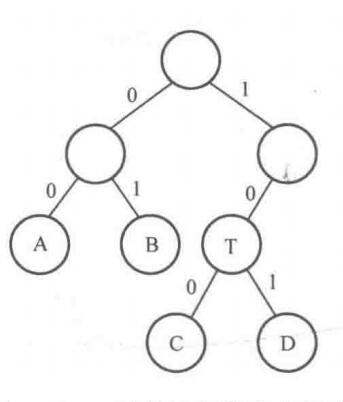
5.3.3.1 哈夫曼编码
哈夫曼编码是指,对于一颗二叉树上的所有节点,都可以用一个唯一的二进制序列来表示。其具体方法就是:从根节点开始到该节点的路径,从根节点开始,选择左子树就添加0,选择右子树就添加1,这样最后的序列就是该节点的序列。如:
中,C的哈夫曼编码就是100,D的哈夫曼编码是101。
5.4 图
5.4.1 最短路径
在PAT考试中,Dijkstra单源最短路就够用了,这里只介绍此算法,其他的后续再更新。
此算法使用稀疏数组表示图,设置数组d,d[i]表示从起点到点i的最小距离,初始化d中所有元素的值为最大值INF。
下面直接给出实现,具体思路可以看:数据结构图之最短路 Dijkstra
const int INF = 0x3f;
int mp[MAXN][MAXN];
int d[MAXN];
int used[MAXN];
int V; // 顶点数量
// 计算从点s开始到其他所有点的距离,保存到数组d中
void Dijkstra(int s) {
fill(d, d+V, INF);
fill(used, used+V, 0);
d[s] = 0;
for(int i = 0; i < V; i++) {
int v = -1;
for(int j = 0; j < V; j++) { // 找出没有使用的,距离最近的点
if ((v < 0 || d[j] < d[v]) && !used[j]) {
v = j;
}
}
if (v < 0) break; // 所有点使用完
for (int u = 0; u < V; u++) {
// 到点u的最短路径为当前值与s到v的距离加上v到u的距离的最小值
d[u] = min(d[u], d[v] + mp[v][u]);
}
}
}
5.4.2 连通分量
连通分量的求法依赖于图的遍历,具体方法为:设置used数组记录每个点是否使用。每次在used中找出一个没有使用过的点,通过该点进行图的遍历,将遍历到的点都记录已经使用,再重复此步骤,图的遍历的次数就是连通分量的个数。
图的遍历使用bfs或dfs或dijkstra都可以。
5.5 动态规划
同样PAT已经不再考,不详细介绍,有兴趣可见博文:从斐波那契到01背包,我理解的DP
6. 结语
由于目标是PAT,且作为笔记与模板,检验自己的数据结构知识的系统性,没有太多的涉及原理证明等过程,想要帮助理解可以看胡凡的《算法笔记》,在总结过程中我也大量借鉴了其代码与目录结构,甚至你可以将本文当作此书的有的放矢的精简的读书笔记。
写下这篇总结,希望在作为个人笔记的同时,也能给更多人带来帮助。
若有错误地方可以留言给我。