数据结构编程笔记十八：第七章 图 图的邻接矩阵存储表示及各基本操作的实现

上次我们介绍了赫夫曼的实现，这次介绍图这一章的第一个程序—— 图的邻接矩阵存储表示各基本操作的实现。

还是老规矩：

程序在码云上可以下载。
地址：https://git.oschina.net/601345138/DataStructureCLanguage.git

图相比于树真是麻烦不少：从一对多逻辑关系变成了多对多。各项操作的复杂度都有了很大的提升。

图究竟可以做哪些操作？先看看ADT定义：

ADT Graph {

    数据对象V：V是具有相同特性的数据元素的集合，称为顶点集。
    数据关系R：
            R = {VR}
            VR = {| v,w∈V 且 P(v,w), 表示从 v 到 w 的弧。
                        谓词 P(v,w) 定义了弧 的意义或信息。}
    基本操作P:
        CreatGraph(&G, V, VR);
        //初始条件：V是图的顶点集，VR是图中弧的集合。 
        //操作结果：按V和VR的定义构造图G。 

        DestroyGraph(&G);
        //初始条件：图G存在。 
        //操作结果：销毁图G。 

        LocateVex(G, u);
        //初始条件：图G存在，u和G中顶点有共同特征 
        //操作结果：若G中存在顶点u，则返回该顶点在图中位置；否则返回其它信息。

        GetVex(G, v);
        //初始条件：图G存在，v是G中某个顶点。 
        //操作结果：返回v的值。

        PutVex(&G, v, value);
        //初始条件：图G存在，v是G中某个顶点。 
        //操作结果：对v赋值value。

        FirstAdjVex(G, v); 
        //初始条件：若图G存在，v是G中的某个顶点。 
        //操作结果：返回v的第一个邻接点。若该顶点在G中没有邻接点，则返回空。

        NextAdjVex(G, v, w);
        //初始条件：图G存在， v是G中的某个顶点，w是v的邻接顶点。 
        //操作结果：返回v的（相对于w的）下一个邻接点。
                    若w是v的最后一个邻接点，则返回空。

        InsertVex(&G, v); 
        //初始条件：图G存在，v和图中的顶点有相同特征。 
        //操作结果：在图G中增添新顶点v。

        DeleteVex(&G, v);
        //初始条件：图G存在，v和w是G中的两个顶点 
        //操作结果：删除G中顶点v及其相关的弧。

        InsertArc(&G, v, w); 
        //初始条件：图G存在，v和w是G中的两个顶点。 
        //操作结果：在G中增添弧，若G是无向的，则还增添对称弧。

        DeleteArc(&G, v, w);
        //初始条件：图G存在，v和w是G中的两个顶点。  
        //操作结果：在G中删除弧，若G是无向的，则还删除对称弧。

        DFSTraverse(G, v, Visit());
        //初始条件：图G存在，Visit是顶点的函数。 
        //操作结果：对图进行深度优先遍历，在遍历过程中对每个顶点调用函数
                    Visit一次且仅一次。一旦Visit失败则操作失败。 

        BFSTraverse(G, v, Visit());
        //初始条件：图G存在，Visit是顶点的应用函数。 
        //操作结果：对图进行广度优先遍历，在遍历过程中对每个顶点调用函数
                    Visit一次且仅一次。一旦Visit失败则操作失败。 
}ADT Graph

书上介绍了图的四种存储结构，但我们只实现其中两种——邻接矩阵和邻接表，为图这一章后面的算法实现打好基础。

这一次先介绍图的邻接矩阵表示法——用矩阵表示顶点的邻接关系，用二维数组存储矩阵。就像这样：

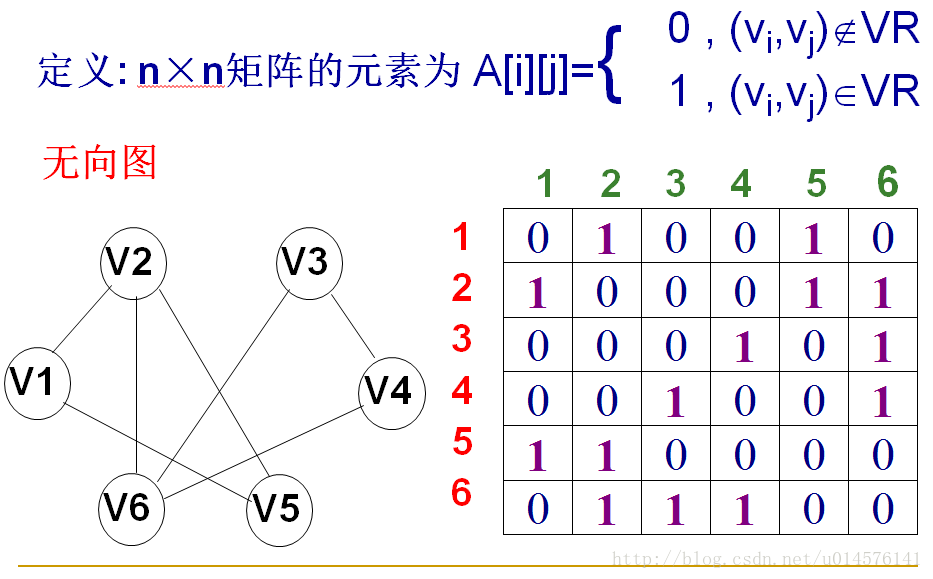
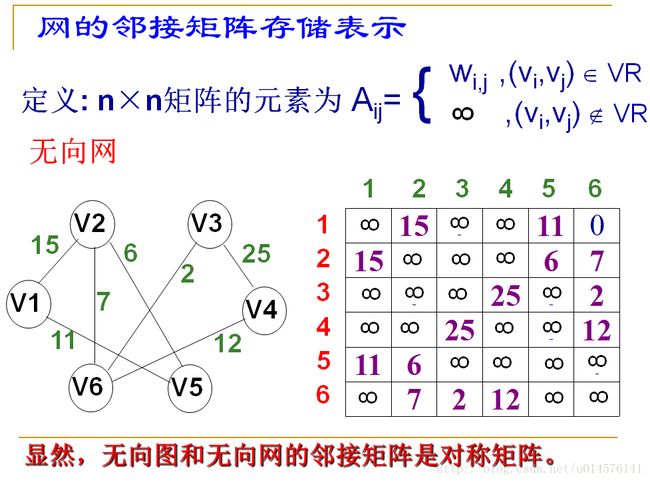
本次程序用到的源文件清单：
my_constants.h 各种状态码
MGraph.h 图的邻接矩阵存储结构表示定义
MGraph.cpp 基于邻接矩阵的基本操作实现
DFS_BFS_Traverse_MGraph.cpp 基于邻接矩阵的深度优先遍历和广度优先遍历算法实现
SqQueue.cpp 顺序队列（循环队列）的实现
基本操作及遍历测试.cpp 主函数，调用基本操作完成演示

注意：所有源文件需放在同一个目录下编译。

本次程序的广度优先遍历用到了队列，我使用了第三章的程序：循环队列。
循环队列在《数据结构编程笔记十：第三章 栈和队列 循环队列的实现》一文中有介绍。
具体程序我放在总结后面。如有需要请到那里查看。

需要注意的是：我对书上P161页的存储结构做了改造，去掉了info指针。
原因是：邻接矩阵中info指针完全没必要设置，因为无论是图还是网，adj这个数据域都已经足够存储所有有用信息了。adj可以不像邻接表一样存储邻接点，因为它已经隐含在邻接矩阵的列名中了。作者设置info指针的本意是指向存储网权值的内存空间。但是由于邻接矩阵中的adj本身就能存储网中的权值，也不会引起歧义，而且设置了info之后还会涉及很多内存的分配、释放和指针操作。为了使一个函数适用于四种图，需要根据图的不同类型对这个指针执行不同的操作。去掉info可以简化很多操作。

接下来一起看看源码实现吧！

源文件：my_constants.h

//************************自定义符号常量*************************** 

#define OVERFLOW -2         //内存溢出错误常量
#define OK 1                //表示操作正确的常量 
#define ERROR 0             //表示操作错误的常量
#define TRUE 1              //表示逻辑真的常量 
#define FALSE 0             //表示逻辑假的常量

//***********************自定义数据类型****************************

typedef int Status;        //指定状态码的类型是int 

源文件：MGraph.h

//-------------图的数组（邻接矩阵）存储表示

//一个输入的权值很难达到的最大值 ∞
#define INFINITY 65535

//最大顶点个数
#define MAX_VERTEX_NUM 20

//使用枚举类型定义图的四种基本类型 
typedef enum {

    //（有向图=0，有向网=1，无向图=2，无向网=3）
    DG, DN, UDG, UDN
} GraphKind;

//指定顶点关系类型为int 
typedef int VRType;

//指定顶点类型为int 
typedef int VertexType;

typedef struct ArcCell{

    //VRType是顶点关系类型。
    //对无权图，用1或0，表示相邻与否，对带权图，则为权值类型 
    VRType adj;

    //我修改了书上的定义删除了info指针。
    //原因是：info指针完全没必要设置，因为无论是图还是网，
    //        adj这个数据域都已经足够存储所有有用信息了。
    //        作者设置info指针的本意是指向存储网权值的内存空间。
    //        但是由于adj本身就能存储网中的权值，也不会引起歧义
    //        而且设置了info之后还会涉及很多内存的分配、释放和指针操作
    //        为了使一个函数适用于四种图，需要根据图的不同类型对这个指针
    //        执行不同的操作。去掉info可以简化操作。 

}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; 

typedef struct{

    //顶点向量:存储了图中所有的顶点 
    VertexType vexs[MAX_VERTEX_NUM];

    //邻接矩阵：存储了顶点之间的邻接关系以及权值 
    AdjMatrix arcs; 

    //图当前的顶点数和弧数
    int vexnum, arcnum;

    //图的种类标志 
    GraphKind kind;
}MGraph; 

源文件：MGraph.cpp

/*
    函数：LocateVex
    参数：MGraph G 图G（邻接矩阵存储结构） 
    返回值：若G中存在顶点v，则返回该顶点在图中位置；否则返回-1
    作用：顶点定位函数，在图G中查找顶点v的位置 
*/
int LocateVex(MGraph G, int v){

    //遍历邻接矩阵查找顶点v 
    for(int i = 0; i <= G.vexnum; ++i) { 

        //若找到结点返回i
        if(G.vexs[i] == v) {
            return i;
        }//if 
    }//for

    //否则返回-1，表示没有找到 
    return -1;
}//LocateVex

/*
    函数：CreateUDN
    参数：MGraph &G 图的引用 
    返回值：状态码，操作成功返回OK 
    作用：采用数组（邻接矩阵）表示法，构造无向网G
*/
Status CreateUDN(MGraph &G){

    //临时变量，从键盘接收顶点名称 
    VertexType v1, v2;

    //临时变量i用于保存顶点v1在图中的序号
    //临时变量j用于保存顶点v2在图中的序号 
    //临时变量w用于接收输入的权值 
    int w, i, j;

    //确定无向网的顶点数和边数 
    printf("请依次输入无向网G的顶点数，弧数，用逗号隔开\n");
    scanf("%d,%d", &G.vexnum, &G.arcnum);

    //从键盘输入各个顶点以构造各顶点向量 
    printf("请依次输入无向网G的顶点名称，用空格隔开\n"); 
    for(int i = 0; i < G.vexnum; ++i) { 
        scanf("%d", &G.vexs[i]);
    }//for

    //初始化邻接矩阵各存储单元的值为INFINITY，INFINITY表示两顶点不可达 
    for(int i = 0; i < G.vexnum; ++i) { 
        for(int j = 0; j < G.vexnum; ++j) { 
            G.arcs[i][j].adj = INFINITY;
        }//for 
    }//for

    //输入弧依附的顶点和权值，填充邻接矩阵  
    printf("请依次输入无向网G每条弧依附的两顶点名称及权值，输完一组按回车\n"); 
    for(int k = 0; k < G.arcnum; ++k){

        //输入弧依附的两顶点v1和v2 
        scanf("%d", &v1);
        scanf("%d", &v2);

        //输入弧上的权值 
        scanf("%d", &w);

        //确定v1,v2在G中的位置i,j 
        i = LocateVex(G, v1);
        j = LocateVex(G, v2);

        //保存权值到邻接矩阵的对应存储单元中 
        G.arcs[i][j].adj = w;

        //由于构造的是无向网，所以还需要置的对称弧 
        //技巧：结构体直接赋值相当于结构体中各个分量的对应拷贝 
        G.arcs[j][i] = G.arcs[i][j];
    }//for

    //操作成功 
    return OK; 
}// CreateUDN

/*
    函数：CreateUDG
    参数：MGraph &G 图的引用 
    返回值：状态码，操作成功返回OK 
    作用：采用数组（邻接矩阵）表示法，构造无向图G 
*/
Status CreateUDG(MGraph &G){

    //接收用户从键盘输入的顶点 
    VertexType v1, v2;

    //临时变量i用于保存顶点v1在图G中的序号
    //临时变量j用于保存顶点v2在图G中的序号  
    int i, j;

    //确定无向图的顶点数和边数，用作循环控制边界 
    printf("请依次输入无向图G的顶点数，弧数，用逗号隔开\n");
    scanf("%d,%d", &G.vexnum, &G.arcnum);

    //输入各顶点名称并构造各顶点向量 
    printf("请依次输入无向图G的顶点名称，用空格隔开\n"); 
    for(int i = 0; i < G.vexnum; ++i) {
        scanf("%d", &G.vexs[i]);
    }//for

    //初始化邻接矩阵所有存储单元的值为0，0表示两顶点之间不可达 
    for(int i = 0; i < G.vexnum; ++i) {
        for(int j = 0; j < G.vexnum; ++j) {
            G.arcs[i][j].adj = 0;
        }//for
    }//for 

    //输入弧依附的顶点，填充邻接矩阵  
    printf("请依次输入无向图G每条弧依附的两顶点名称，输完一组按回车\n"); 
    for(int k = 0; k < G.arcnum; ++k){

        //输入弧依附的两顶点v1和v2  
        scanf("%d", &v1);
        scanf("%d", &v2);

        //确定v1,v2在G中的位置i和j 
        i = LocateVex(G, v1);
        j = LocateVex(G, v2);

        //设置v1->v2的值为1，表示v1->v2是可达的 
        G.arcs[i][j].adj = 1;

        //由于构造的是无向图，所以还需要置的对称弧
        G.arcs[j][i] = G.arcs[i][j]; 
    }//for

    //操作成功 
    return OK; 
}// CreateUDG

/*
    函数：CreateDN
    参数：MGraph &G 图的引用 
    返回值：状态码，操作成功返回OK 
    作用：采用数组（邻接矩阵）表示法，构造有向网G 
*/
Status CreateDN(MGraph &G){

    //临时变量v1和v2用于接收从键盘输入的两顶点的值 
    VertexType v1, v2;

    //临时变量w用于保存用户输入的权值
    //临时变量i用于保存顶点v1在图中的位置
    //临时变量j用于保存顶点v2在图中的位置 
    int w, i, j;

    //确定有向网的顶点数和边数，用作循环控制边界 
    printf("请依次输入有向网G的顶点数，弧数，用逗号隔开\n");
    scanf("%d,%d", &G.vexnum, &G.arcnum);

    //输入顶点名称构造各顶点向量
    printf("请依次输入有向网G的顶点名称，用空格隔开\n"); 
    for(int i = 0; i < G.vexnum; ++i) { 
        scanf("%d", &G.vexs[i]);
    }//for 

    //初始化邻接矩阵各存储单元的值为INFINITY，INFINITY表示两顶点不可达 
    for(int i = 0; i < G.vexnum; ++i) { 
        for(int j = 0; j < G.vexnum; ++j) { 
            G.arcs[i][j].adj = INFINITY;
        }//for
    }//for

    //输入弧依附的顶点和权值，填充邻接矩阵 
    printf("请依次输入有向网G每条弧依附的两顶点名称及权值，输完一组按回车\n"); 
    for(int k = 0; k < G.arcnum; ++k) {

        //输入弧依附的两顶点v1和v2 
        scanf("%d", &v1);
        scanf("%d", &v2);

        //输入弧上的权值 
        scanf("%d", &w);

        //确定v1,v2在G中的位置 
        i = LocateVex(G, v1);
        j = LocateVex(G, v2);

        //保存权值到邻接矩阵的对应存储单元中      
        G.arcs[i][j].adj = w;
    }//for

    //操作成功 
    return OK; 
}// CreateDN

/*
    函数：CreateDG
    参数：MGraph &G 图的引用 
    返回值：状态码，操作成功返回OK 
    作用：采用数组（邻接矩阵）表示法，构造有向图G  
*/
Status CreateDG(MGraph &G){

    //临时变量v1和v2用于接收从键盘输入的两顶点的值 
    VertexType v1, v2;

    //临时变量i用于保存顶点v1在图中的位置
    //临时变量j用于保存顶点v2在图中的位置 
    int i, j;

    //确定有向网的顶点数和边数，用作循环控制边界 
    printf("请依次输入有向图G的顶点数，弧数，用逗号隔开\n");
    scanf("%d,%d", &G.vexnum, &G.arcnum);

    //输入顶点名称构造各顶点向量
    printf("请依次输入有向图G的顶点名称，用空格隔开\n"); 
    for(int i = 0; i < G.vexnum; ++i) { 
        scanf("%d", &G.vexs[i]);
    }//for

    //初始化邻接矩阵所有存储单元的值为0，0表示两顶点之间不可达  
    for(int i = 0; i < G.vexnum; ++i) {
        for(int j = 0; j < G.vexnum; ++j) {
            G.arcs[i][j].adj=0; 
        }//for
    }//for

    //输入弧依附的顶点，填充邻接矩阵 
    printf("请依次输入有向图G每条弧依附的两顶点名称，输完一组按回车\n"); 
    for(int k = 0; k < G.arcnum; ++k) { 

        //输入弧依附的两顶点v1和v2 
        scanf("%d", &v1);
        scanf("%d", &v2);

        //确定v1,v2在G中的位置i和j 
        i = LocateVex(G, v1);
        j = LocateVex(G, v2);

        //设置v1->v2的值为1，表示v1->v2是可达的
        G.arcs[i][j].adj = 1;
    }//for

    //操作成功 
    return OK; 
}// CreateDG

/*
    函数：CreateGraph
    参数：MGraph &G 图的引用 
    返回值：状态码，操作成功返回OK 
    作用：采用数组（邻接矩阵）表示法，构造图G
*/
Status CreateGraph(MGraph &G){

    //输入构造图的类型 
    printf("请输入您想构造的图的类型:有向图输入0,有向网输入1,无向图输入2,无向网输入3):");
    scanf("%d", &G.kind);

    //根据图的不同类型调用图的构造函数 
    switch(G.kind){
        case  DG:  return CreateDG(G);  //构造有向图G
        case  DN:  return CreateDN(G);  //构造有向网G
        case UDG:  return CreateUDG(G); //构造无向图G
        case UDN:  return CreateUDN(G); //构造无向网G
        default :  return ERROR;
    }//switch
}//CreateGraph

/*
    函数：DestroyGraph
    参数：MGraph &G 图的引用 
    返回值：状态码，操作成功返回OK 
    作用：销毁图G
*/
Status DestroyGraph(MGraph &G) {

    //若是网 
    if(G.kind % 2) {

        //重置邻接矩阵所有顶点之间不可达 
        for(int i = 0; i < G.vexnum; i++) {
            for(int j = 0; j < G.vexnum; j++) {
                G.arcs[i][j].adj = INFINITY;
            }//for 
        }//for 
    }//if
    else { //若是图 

        //重置邻接矩阵所有顶点之间不可达 
        for(int i = 0; i < G.vexnum; i++) {
            for(int j = 0; j < G.vexnum; j++) {
                G.arcs[i][j].adj = 0;
            }//for 
        }//for 
    }//else

    //重置顶点数为0
    G.vexnum = 0;

    //重置边数为0
    G.arcnum = 0;
}//DestroyGraph

/*
    函数：PrintAdjMatrix
    参数：MGraph G 图G
    返回值：状态码，操作成功返回OK 
    作用：打印某个图的邻接矩阵 
*/
Status PrintAdjMatrix(MGraph G){

    //输出左上角多余的空白 
    printf("      ");

    //输出邻接矩阵的上坐标（全部顶点） 
    for(int i = 0; i < G.vexnum; i++) {

        printf(" %3d ", G.vexs[i]);     
    }//for 

    printf("\n"); 

    //输出左上角多余的空白 
    printf("     +");

    //输出一条横线
    for(int i = 0; i < G.vexnum; i++) {
        printf("-----"); 
    }//for 

    printf("\n"); 

    //输出邻接矩阵的左坐标（全部顶点）和内容 
    for(int i = 0; i < G.vexnum; i++) {

        //输出邻接矩阵左边的坐标
        printf(" %3d |", G.vexs[i]);  

        for(int j = 0; j < G.vexnum; j++) {
            if(G.arcs[i][j].adj == INFINITY) {
                printf("  ∞ ");
            }//if 
            else {
                printf(" %3d ", G.arcs[i][j].adj);
            }//else
        }//for 
        printf("\n     |\n");
    }//for 
}//PrintAdjMatrix

/*
    函数：GetVex
    参数：MGraph G 图G
          int v v是G中某个顶点的序号
    返回值：返回v的值
    作用：得到序号为v的顶点值 
*/
VertexType& GetVex(MGraph G, int v) {

    //检查参数v是否合法：v是否越界 
    if(v >= G.vexnum || v < 0) { 
        exit(ERROR);
    }//if

    //返回序号为v的顶点值 
    return G.vexs[v];
}//GetVex

/*
    函数：PutVex
    参数：MGraph &G 图的引用 
          VertexType v v是G中某个顶点
          VertexType value 将序号为v的顶点的值修改为value 
    返回值：状态码，操作成功返回OK，否则返回ERROR 
    作用：修改序号为v的顶点值 
*/
Status PutVex(MGraph &G, VertexType v, VertexType value) {

    //k为顶点v在图G中的序号
    int k = LocateVex(G, v);

    //检查图中是否存在顶点v
    if(k < 0) { 
        return ERROR;
    }//if

    //将顶点v的值置为value 
    G.vexs[k] = value;

    //操作成功 
    return OK;
}//PutVex 


/*
    函数：FirstAdjVex
    参数：MGraph G 图G
          VertexType v 顶点v 
    返回值：若找到邻接点，返回邻接点的顶点位置，否则返回-1 
    作用：求顶点v在图G中的第一个邻接点
*/
int FirstAdjVex(MGraph G, VertexType v){

    //j表示不可达，在图中，0表示不可达，在网中INFINITY表示不可达 
    int j = 0;

    //v是顶点，不是序号！需要定位 
    //k就是顶点v在顶点数组中的序号 
    int k = LocateVex(G, v);

    //若是网，则INFINITY表示不可达 
    if(G.kind == DN || G.kind == UDN) {
       j = INFINITY;
    }//if

    //在顶点v对应的第k行查找第一个邻接点的序号i 
    for(int i = 0; i < G.vexnum; ++i) {

        //若找到顶点v的第一个邻接点则返回i
        //G.arcs[k][i].adj != j 表示顶点G.arcs[k][i]可达 
        if(G.arcs[k][i].adj != j) {
            return i;
        }//if 
    }//for

    //若未找到返回-1 
    return -1;
}//FirstAdjVex

/*
    函数：NextAdjVex
    参数：MGraph G 图G
          VertexType v 顶点v 
    返回值：若找到邻接点，返回邻接点的顶点位置，否则返回-1 
    作用：求顶点v在图G中相对于邻接点w的下一个邻接点
*/
int NextAdjVex(MGraph G, VertexType v, VertexType w){

    //j表示不可达，在图中，0表示不可达，在网中INFINITY表示不可达
    int j = 0;

    //k1是顶点v在顶点数组中的位序 
    int k1 = LocateVex(G, v);

    //k2是顶点w在顶点数组中的位序 
    int k2 = LocateVex(G, w);

    //若是网，则使用INFINITY表示不可达 
    if(G.kind == DN || G.kind == UDN) { 
        j = INFINITY;
    }//if

    //在图G中查找顶点v相对于顶点w的下一个邻接点的位置 
    for(int i= k2 + 1; i < G.vexnum; ++i) {

        //若找到则返回i 
        if(G.arcs[k1][i].adj != j) {
            return i;
        }//if
    }//for

    //若未找到返回-1
    return -1;
}//NextAdjVex

/*
    函数：InsertVex
    参数：MGraph &G 图的引用 
          VertexType v 顶点v 
    返回值：状态码，操作成功返回OK 
    作用：在图G中增添新顶点v
*/
Status InsertVex(MGraph &G, VertexType v) {

    //j表示不可达，在图中，0表示不可达，在网中INFINITY表示不可达
    int j = 0;

    //若是网，则使用INFINITY表示不可达 
    if(G.kind % 2) { 
        j = INFINITY;
    }//if

    //构造新顶点向量
    G.vexs[G.vexnum] = v;

    //初始化邻接矩阵 
    for(int i = 0; i <= G.vexnum; i++) {

        //初始化矩阵的每个存储单元为不可达 
        G.arcs[G.vexnum][i].adj = G.arcs[i][G.vexnum].adj = j;
    }//for

    //图G的顶点数加1
    G.vexnum++;

    //操作成功 
    return OK; 
}//InsertVex

/*
    函数：DeleteVex
    参数：MGraph &G 图的引用 
          VertexType v 顶点v 
    返回值：状态码，操作成功返回OK 
    作用：删除G中顶点v及其相关的弧
*/
Status DeleteVex(MGraph &G, VertexType v) {

    //m表示不可达，在图中，0表示不可达，在网中INFINITY表示不可达
    VRType m = 0;

    //若是网，则使用INFINITY表示不可达 
    if(G.kind % 2) {
        m = INFINITY;
    }//if

    //k为待删除顶点v的序号
    int k = LocateVex(G, v);

    //检查v是否是图G的顶点
    if(k < 0) { //v不是图G的顶点

        //操作失败 
        return ERROR;
    }//if

    //删除边的信息 
    for(int j = 0; j < G.vexnum; j++) { 

        //有入弧
        if(G.arcs[j][k].adj != m) {

            //删除弧
            G.arcs[j][k].adj = m; 

            //弧数-1
            G.arcnum--; 
        }//if

        //有出弧
        if(G.arcs[k][j].adj != m) {

            //删除弧
            G.arcs[k][j].adj = m; 

            //弧数-1
            G.arcnum--;
        }//if 
    }//for 

    //序号k后面的顶点向量依次前移
    for(int j = k + 1; j < G.vexnum; j++) {
        G.vexs[j-1] = G.vexs[j];
    }//for

    //移动待删除顶点之右的矩阵元素
    for(int i = 0; i < G.vexnum; i++) {
        for(int j = k + 1; j < G.vexnum; j++) {
            G.arcs[i][j - 1] = G.arcs[i][j];
        }//for
    }//for

    //移动待删除顶点之下的矩阵元素
    for(int i = 0; i < G.vexnum; i++) {
        for(int j = k + 1; j < G.vexnum; j++) {
            G.arcs[j - 1][i] = G.arcs[j][i];
        }//for
    }//for

    //图的顶点数-1
    G.vexnum--;

    //操作成功 
    return OK;
}//DeleteVex

/*
    函数：InsertArc
    参数：MGraph &G 图的引用 
          VertexType v 顶点v（弧尾） 
          VertexType w 顶点w（弧头） 
    返回值：状态码，操作成功返回OK 
    作用：在G中增添弧，若G是无向的，则还增添对称弧
*/
Status InsertArc(MGraph &G, VertexType v, VertexType w) {

    //弧尾顶点v在图中的序号v1 
    int v1 = LocateVex(G, v);

    //弧头顶点w在图中的序号w1 
    int w1 = LocateVex(G, w);

    //检查顶点v和顶点w在图中是否存在 
    if(v1 < 0 || w1 < 0) {  //v或w有一个不是图G中的顶点

        //操作失败 
        return ERROR;
    }//if 

    //弧或边数加1
    G.arcnum++;

    //如果是图G是网，还需要输入权值 
    //if(G.kind % 2) <=> if(G.kind % 2 != 0)
    if(G.kind % 2) {
        printf("请输入此弧或边的权值: ");
        scanf("%d", &G.arcs[v1][w1].adj);
    }//if
    else { // 图
        G.arcs[v1][w1].adj = 1;
    }//else 

    //如果是无向图或无向网还需要置对称的边 
    if(G.kind > 1) {
        G.arcs[w1][v1].adj = G.arcs[v1][w1].adj;
    }//if

    //操作成功 
    return OK;
}//InsertArc

/*
    函数：DeleteArc
    参数：MGraph &G 图的引用 
          VertexType v 顶点v（弧尾） 
          VertexType w 顶点w（弧头） 
    返回值：状态码，操作成功返回OK，操作失败返回ERROR 
    作用：在G中删除弧，若G是无向的，则还删除对称弧
*/
Status DeleteArc(MGraph &G, VertexType v, VertexType w) {

    //j表示不可达，在图中，0表示不可达，在网中INFINITY表示不可达
    int j = 0;

    //若是网，则使用INFINITY表示不可达 
    if(G.kind % 2) {
        j = INFINITY;
    }//if

    //弧头顶点v在图中的序号v1 
    int v1 = LocateVex(G, v);

    //弧尾顶点w在图中的序号w1 
    int w1 = LocateVex(G, w);

    //检查顶点v和顶点w在图中是否存在 
    if(v1 < 0 || w1 < 0) { //v或w有一个不是图G中的顶点
        return ERROR;
    }//if 

    //将顶点v与顶点w之间设为不可达 
    G.arcs[v1][w1].adj = j;

    //如果是无向图或网，还需要删除对称弧
    if(G.kind >= 2) {
        G.arcs[w1][v1].adj = j;
    }//if

    //弧数-1
    G.arcnum--;

    //操作成功 
    return OK;
}//DeleteArc

源文件：DFS_BFS_Traverse_MGraph.cpp

//-----------------------深度优先遍历DFS-----------------------------

//访问标志数组 
int visited[MAX_VERTEX_NUM];

//函数变量 
Status (*VisitFunc)(int v);

/*
    函数：Print
    参数：int v 被访问的顶点v 
    返回值：状态码，操作成功返回OK，操作失败返回ERROR 
    作用：元素访问函数
*/
Status Print(int v){

    //设置元素访问方式为控制台打印 
    printf(" %3d ", v);

    //操作成功 
    return OK;
}//Print

/*
    函数：DFSTraverse
    参数：MGraph G 图G
          int v 从序号为v的顶点出发 
    返回值：无
    作用：从第v个顶点出发递归地深度优先遍历图G
*/
void DFS(MGraph G, int v){

    //先将访问标志数组该元素的访问标志改为True，
    //含义是序号为v的顶点已被访问 
    visited[v] = TRUE;

    //访问第v个顶点
    VisitFunc(G.vexs[v]);

    //依次访问v的各个邻接顶点（向v的邻接点延伸） 
    for(int w = FirstAdjVex(G, G.vexs[v]); w >= 0; 
            w = NextAdjVex(G, G.vexs[v], G.vexs[w])){

        //对v的尚未被访问的邻接点w递归调用DFS 
        if(!visited[w]) { 
            DFS(G, w);
        }//if 
    }//for
}//DFS

/*
    函数：DFSTraverse
    参数：MGraph G 图G
          Status (*Visit)(int v) 函数指针，指向元素访问函数 
    返回值：无
    作用：对图G作深度优先遍历,调用Visit()函数访问结点
*/
void DFSTraverse(MGraph G, Status (*Visit)(int v)){

    //使用全局变量VisitFunc，使DFS不必设函数指针参数 
    VisitFunc = Visit;

    //预置标志数组visited所有值为FALSE 
    for(int v = 0; v < G.vexnum; ++v) { 
        visited[v] = FALSE;
    }//for

    //深度优先遍历主循环 
    //写成循环是为了保证在图分为多个连通分量时能对
    //每个连通分量进行遍历 
    for(int v = 0; v < G.vexnum; ++v) {

        //若该顶点未被访问，则调用DFS()访问该节点
        if(!visited[v]) {
            DFS(G, v); 
        }//if
    }//for 
}//DFSTraverse

//----------------广度优先遍历 (需要使用队列)BFS------------ 
//说明：队列的相关代码包含在"SqQueue.cpp"中，关于队列的详细方法请阅读该文件

/*
    函数：BFSTraverse
    参数：MGraph G 图G
          Status (*Visit)(int v) 函数指针，指向元素访问函数 
    返回值：无
    作用：按广度优先非递归遍历图G，使用辅助队列Q和访问标志数组visited
*/ 
void BFSTraverse(MGraph G, Status (*Visit)(int v)){

    int u;

    //广度优先遍历使用到遍历 
    SqQueue Q;

    //预置标志数组visited所有值为FALSE 
    for(int v = 0; v < G.vexnum; ++v) { 
        visited[v] = FALSE;
    }//for 

    //初始化辅助队列Q，得到一个空队列 
    InitQueue_Sq(Q);

    //广度优先遍历主循环 
    for(int v = 0; v < G.vexnum; ++v) {

        //v尚未访问
        if(!visited[v]){

            //设置v已经被访问 
            visited[v] = TRUE;

            //访问第v顶点
            Visit(G.vexs[v]);

            //v入队列
            EnQueue_Sq(Q, v);

            //队列不空 
            while(!QueueEmpty_Sq(Q)){

                //队头元素出队并置为u
                DeQueue_Sq(Q, u);

                //依次访问第u顶点的邻接顶点 
                for(int w = FirstAdjVex(G, G.vexs[u]); w >= 0;
                        w = NextAdjVex(G, G.vexs[u], G.vexs[w])){ 

                    //w为v尚未访问的邻接顶点
                    if(!visited[w]){ 

                        //设置第w顶点已被访问 
                        visited[w] = TRUE;

                        //访问第w顶点
                        Visit(G.vexs[w]); 
                    }//if 
                }//for 
            }//while 
        }//if
    }//for 

    //销毁循环队列 
    DestoryQueue_Sq(Q);
}//BFSTraverse

源文件：基本操作及遍历测试.cpp

//**************************引入头文件*****************************
#include    //使用了标准库函数 
#include   //使用了动态内存分配函数

#include "my_constants.h" //引入自定义的符号常量，主要是状态码 
#include "SqQueue.cpp"    //由于广度优先遍历要使用队列，插入删除少访问多，故引入顺序队列 
#include "MGraph.h"       //引入图的邻接矩阵表示法的基本定义 
#include "MGraph.cpp"     //引入图的主要操作
#include "DFS_BFS_Traverse_MGraph.cpp" //引入图的深度优先和广度优先遍历算法实现 


//----------------------主函数----------------------
int main(int argc, char *argv[]){

    printf("\n-------------图的邻接矩阵表示法基本操作测试程序--------------\n\n"); 

    //图G 
    MGraph G; 

    //临时变量，保存输入的顶点 
    VertexType v1, v2;

    //临时变量，保存输入的顶点数 
    int n;

    //图的创建
    printf("->测试图的创建：\n");
    CreateGraph(G);

    //打印邻接矩阵
    printf("\n->创建成功后图的邻接矩阵:\n\n"); 
    PrintAdjMatrix(G);

    //测试图的遍历（深度、广度） 
    printf("\n->测试图的遍历:\n");
    printf("->深度优先遍历结果：");
    DFSTraverse(G, Print);

    printf("\n->广度优先遍历结果：");
    BFSTraverse(G, Print);
    printf("\n");

    //测试插入顶点和边的操作 
    printf("\n->测试插入新顶点\n ");
    printf("->请输入顶点的值: ");
    scanf("%d", &v1);
    InsertVex(G, v1);

    printf("->测试插入边\n");
    printf("->插入与新顶点（有向图或网中的弧尾）有关的弧或边，请输入弧或边数: ");
    scanf("%d", &n);
    for(int k = 0; k < n; k++) {

        printf("->请输入另一顶点（弧头）的值: ");
        scanf("%d", &v2);

        //以v1为弧尾,v2为弧头插入弧 
        InsertArc(G, v1, v2);
    }//for

    printf("->插入顶点和弧后图的邻接矩阵:\n\n"); 
    PrintAdjMatrix(G);

    //测试删除顶点 
    printf("\n->删除顶点及相关的弧或边，请输入顶点的值: ");
    scanf("%d", &v1);
    DeleteVex(G, v1);

    printf("->删除顶点和弧后图的邻接矩阵:\n\n"); 
    PrintAdjMatrix(G);

    //测试销毁 
    printf("\n->测试销毁图： ");
    DestroyGraph(G); 
    printf("成功！\n");

    printf("演示结束，程序退出！\n");

    return 0;
} 

测试采用的是书上P174页的无向网。

运行输入的数据以及程序的输出如下：

-------------图的邻接矩阵表示法基本操作测试程序--------------

->测试图的创建：
请输入您想构造的图的类型:有向图输入0,有向网输入1,无向图输入2,无向网输入3):3
请依次输入无向网G的顶点数，弧数，用逗号隔开
6,10
请依次输入无向网G的顶点名称，用空格隔开
1 2 3 4 5 6
请依次输入无向网G每条弧依附的两顶点名称及权值，输完一组按回车
1 2 6
1 4 5
1 3 1
3 2 5
3 4 5
3 5 6
3 6 4
2 5 3
4 6 2
5 6 6

->创建成功后图的邻接矩阵:

         1    2    3    4    5    6
     +------------------------------
   1 |  ∞    6    1    5   ∞   ∞
     |
   2 |   6   ∞    5   ∞    3   ∞
     |
   3 |   1    5   ∞    5    6    4
     |
   4 |   5   ∞    5   ∞   ∞    2
     |
   5 |  ∞    3    6   ∞   ∞    6
     |
   6 |  ∞   ∞    4    2    6   ∞
     |

->测试图的遍历:
->深度优先遍历结果：   1    2    3    4    6    5
->广度优先遍历结果：   1    2    3    4    5    6

->测试插入新顶点
->请输入顶点的值: 7

->测试插入边
 ->插入与新顶点（有向图或网中的弧尾）有关的弧或边，请输入弧或边数: 2
->请输入另一顶点（弧头）的值: 2
请输入此弧或边的权值: 10
->请输入另一顶点（弧头）的值: 5
请输入此弧或边的权值: 15
->插入顶点和弧后图的邻接矩阵:

         1    2    3    4    5    6    7
     +-----------------------------------
   1 |  ∞    6    1    5   ∞   ∞   ∞
     |
   2 |   6   ∞    5   ∞    3   ∞   10
     |
   3 |   1    5   ∞    5    6    4   ∞
     |
   4 |   5   ∞    5   ∞   ∞    2   ∞
     |
   5 |  ∞    3    6   ∞   ∞    6   15
     |
   6 |  ∞   ∞    4    2    6   ∞   ∞
     |
   7 |  ∞   10   ∞   ∞   15   ∞   ∞
     |

->删除顶点及相关的弧或边，请输入顶点的值: 7
->删除顶点和弧后图的邻接矩阵:

         1    2    3    4    5    6
     +------------------------------
   1 |  ∞    6    1    5   ∞   ∞
     |
   2 |   6   ∞    5   ∞    3   ∞
     |
   3 |   1    5   ∞    5    6    4
     |
   4 |   5   ∞    5   ∞   ∞    2
     |
   5 |  ∞    3    6   ∞   ∞    6
     |
   6 |  ∞   ∞    4    2    6   ∞
     |

->测试销毁图： 成功！
演示结束，程序退出！

--------------------------------
Process exited with return value 0
Press any key to continue . . .

总结：就用这样一幅图总结吧，虽然不怎么美观。

                        图变网，加权值，改距离    有向变无向 ，置对称弧结点

                                       加权值  0,1变 ∞ 
                       有向图 <------------------------------> 有向网      
                          |            去权值  ∞变 0,1          | 
                          |                                      |
            去对称弧结点  |  置对称弧结点         去对称弧结点   |   置对称弧结点 
                          |                                      |
                          |            加权值  0,1变 ∞          |
                       无向图 <------------------------------> 无向网
                                       去权值  ∞变 0,1

下次的文章会介绍图的邻接表存储结构的以及基于这种存储结构基本操作的实现。感谢大家的关注，再见！

附：循环队列精简后的源码：

源文件：SqQueue.cpp

//广度优先遍历用到队列的实现 

#define MAXQSIZE 100        //队列的最大长度 
typedef int Status;
typedef int QElemType;

typedef struct {            //循环队列的C语言描述 

    QElemType *base;        //初始化动态分配存储空间
    int front;              //头指针，若队列不空，指向队头元素 
    int rear;               //尾指针，若队列不空，指向队尾元素的下一个位置 
}SqQueue; 

//----------------------循环队列的主要操作------------------------

/*
    函数：InitQueue_Sq
    参数：SqQueue &Q 循环队列引用 
    返回值：状态码，操作成功返回OK 
    作用：构建一个空队列 Q
*/
Status InitQueue_Sq(SqQueue &Q) {

    //申请内存空间，若失败则提示并退出程序
    //if(!(Q.base = (QElemType *)malloc(MAXQSIZE * sizeof(QElemType))))
    //相当于以下两行代码：
    //Q.base = (QElemType *)malloc(MAXQSIZE * sizeof(QElemType))
    //if(!Q.base)  <=>  if(Q.base == NULL)
    if(!(Q.base = (QElemType *)malloc(MAXQSIZE * sizeof(QElemType)))){
        printf("内存分配失败，程序即将退出！\n");
        exit(OVERFLOW);
    }//if

    //由于刚申请的空间没有元素入队，所以队列为空 
    //Q.front == Q.rear是队列为空的标志 
    Q.front = Q.rear = 0;

    //操作成功 
    return OK;
}//InitQueue_Sq

/*
    函数：DestoryQueue_Sq
    参数：SqQueue &Q 循环队列引用 
    返回值：状态码，操作成功返回OK 
    作用：销毁循环队列 Q
*/
Status DestoryQueue_Sq(SqQueue &Q) {

    //循环队列采用连续的存储空间，直接找到首地址释放空间即可 
    if(Q.base) { 
        free(Q.base);
    }//if

    //指针置空，释放掉指针变量本身占用的空间 
    Q.base = NULL;

    //队头和队尾指针归零，队列为空 
    Q.front = Q.rear = 0;

    //操作成功 
    return OK;
}//DestoryQueue_Sq

/*
    函数：QueueEmpty_Sq
    参数：SqQueue Q 循环队列Q 
    返回值：状态码，队列为空返回TRUE，否则返回FALSE 
    作用：判断循环队列 Q是否为空 
*/
Status QueueEmpty_Sq(SqQueue Q) {

    //Q.rear == Q.front是队列为空的标志 
    if(Q.rear == Q.front) { 
        return TRUE; 
    }//if 
    else {
        return FALSE;
    }//else  
}//QueueEmpty_Sq

/*
    函数：EnQueue_Sq
    参数：SqQueue Q 循环队列Q
          QElemType e 被插入元素e 
    返回值：状态码，操作成功返回OK，否则返回ERROR 
    作用：插入元素e为Q的新的队尾元素e  
*/
Status EnQueue_Sq(SqQueue &Q, QElemType e) {

    //由于循环队列使用顺序存储结构，插入时需要判断队列是否满
    //判断队列满的标志：(Q.rear + 1) % MAXQSIZE == Q.front
    if((Q.rear + 1) % MAXQSIZE == Q.front) {  //队列满

        //操作失败 
        return ERROR;
    }//if

    //把e插入到队尾 
    Q.base[Q.rear] = e;

    //每插入一个新队尾元素，尾指针增一
    Q.rear = (Q.rear + 1) % MAXQSIZE;

    //操作成功 
    return OK; 
}//EnQueue_Sq

/*
    函数：DeQueue_Sq
    参数：SqQueue Q 循环队列Q
          QElemType &e 带回被删除的元素e 
    返回值：状态码，操作成功返回OK，否则返回ERROR 
    作用：队列不空,则删除Q的队头元素,用e返回其值
*/
Status DeQueue_Sq(SqQueue &Q, QElemType &e) {

    //在空队列中执行出队操作没有意义，所以要先判断队列是否为空 
    //if(QueueEmpty_Sq(Q)) <=> if(QueueEmpty_Sq(Q) == TRUE)
    if(QueueEmpty_Sq(Q)) { //队列空 

        //操作失败 
        return ERROR;
    }//if

    //保存被删除元素的值 
    e = Q.base[Q.front];

    //每当删除队头元素时，头指针增1 
    Q.front = (Q.front + 1) % MAXQSIZE;

    //操作成功 
    return OK; 
}//DeQueue_Sq