2019独角兽企业重金招聘Python工程师标准>>> ![]()
前言
在一个遥远的国度,有一群毒贩。这些人以贩毒为生,每天贩卖各种毒品。有一天,毒贩们为了更好的服务于他们的客户(当然更本质的原因是为了更大的利润),他们决定统一各种毒品的零售价。这样他们的消费者就不会因为价格不同的原因而四处询价然后只和价格最低的人交易。毒贩之间也不会因为彼此价格不一致而导致用户流失甚至互相明争暗斗。毒贩都是很聪明的人,生活教会了他们很多。
第一个不可行的办法
由一个官方权威组织来统一定价当然是非常简单的措施。比如全体毒贩成立一个毒品物价局,然后由毒品物价局每天来公布各种毒品的价格。比如每天早上,毒品物价局在自己的网站来公布说冰毒5块钱,海洛因20块钱。这样毒贩们每天只要到物价局的网站上来查一下价格就知道自己的零售价了。非常简单、容易,而且不会出错。但是,贩毒这门生意可是不容许这样做的。这可是要掉脑袋的买卖,稍有不小心就会被禁毒的警察们发现。光明正大并且成立统一的组织并公开信息,这绝对是要不得的。这个点子行不通。另外一个原因是,毒贩们都是因为受不了现实生活的约束才走上这样一条自由的道路的。由一个不明来路的物价局来决定我的货的价格,凭什么呢?每个精明而又富有海盗精神的毒贩都绝不会接受这样的做法。如果这样我还做什么买卖,我还不如考公务员呢。毒贩们决定不仅需要统一价格,而且每个毒贩都必须具备定价权。如果毒贩小王认为冰毒卖5块钱最合适,那么这个市场上5块钱就是最适合的价格,其他人也应该卖5块钱。嗯,毒贩们都是大公无私的,他们不仅要自己利益最大化,也要所有同行的利益最大化。
第一个可行的办法
这怎么办呢?精明而又有创意的毒贩们想出了一个既安全又好用的办法。他们雇佣了一个脑子好使的人。这个脑子好使的人有好几项特异功能。比如,他他可以记住毒品的最新的价格而永远不会忘记,而且也不会记错。因为价格全部在他的脑袋里面,警察不会查到任何的证据。当然这只是他的特异功能之一。他还有其他的特异功能,后面用上的时候我们再说。有了这个脑子好使的人帮忙之后,毒贩们的工作变得轻松和愉快了起来。在想要知道某个货物的售价的时候,他们只需要打个电话给这个脑子好使的人问他最新的价格是多少。而如果某个毒贩认为某个毒品的价格需要修改的时候,他也只需要打电话把最新的价格告诉给这个脑子好使的人。这样其他所有的同行,也就能得知最新的价格,而不会受到任何的损失。
第二个可行的办法
这样的工作模式延续了一些日子。这段日子是一段黄金的岁月。毒贩们每天只需要和这个脑子好使的人打打电话就能解决以前靠打打杀杀才解决的难题。对与毒贩来说,这是一段非常轻松愉快的生活。每天工作完之后互相约着喝喝酒,打打高尔夫,好不快活。可是好日子总是不能延续多久。这样的工作模式也有缺陷。因为人不是机器,人都有要休息的时候。有一天这个脑子好使的人生病了没法工作,导致整个毒品网络直接崩溃了。还有一天这个脑子好使的人家里的电话坏了,导致所有的毒贩都不能联系到他,又是崩溃的一天。利润上的损失就不提了,更关键的是那些消费者。一天不吃饭可以,可是如果一天如果没有毒品那可是要命啊。有的毒贩甚至被他们平日里的消费者堵在家里堵了一天一夜差点酿成一些不可描述的事情,直到这个脑子好使的人又可以工作了之后又可以进行交易了这些消费者才喋喋不休的退去。因此,对于毒贩来说这必须立即想办法解决这样的难题。只有一个脑子好使的人的话,他可能会生病、会出现意外状况,甚至可能被警察抓走也可能自己不想干了偷偷逃走(相信毒贩们才不会给他这个机会的),当然作为一个普通人,他也时刻面临去见马克思的风险。于是毒贩们决定多雇佣几个脑子好使的人。这样即使有一个或几个人出现了什么意外的状况,不至于整个生意都没法做了。但是如果这样做,就会面临另外一个问题,那就是这几个脑子好使的人如果他们对于某个货物的价格不一致那么该怎么办呢?毒贩们在一起开会,一直开了3天3夜,这段时间他们不停的讨论以及询问身边的一些聪明的人,直到最后他们想到了一个办法解决这个问题。
他们这个办法是这样的:
1. 每个货物现在除了价格之外,还有一个价格的版本号。每个货物的价格的版本号就是一个数字,例如1 2 3 4 5 等等。会不断的增加。每个脑子好使的人,除了要记住这些货物的价格之外,还需要记住价格的版本号。这些脑子好使的人都是有特殊功能的人,多记忆这么一点点东西对他们来说不算什么。
2. 现在有了很多个脑子好使的人,如果这些人给出的价格不一样,那么就采用少数服从多数的原则。如果超过半数的脑子好使的人报出了同一个价格,那么我们就卖这个价格。
3. 当一个毒贩需要修改某个毒品的价格的时候,他还是只需要打电话给任意一个脑子好使的人。这个脑子好使的人需要把这个价格传递给他的其他的同事。因为这些脑子好使的人他们还有一个特异功能,那就是脑电波传输。无论彼此之间距离相隔多远,他们都能通过脑电波把消息传递给他们的同类。只不过有的时候,这种传递的方式不是那么靠谱。这些脑电波可能会因为一些诡异的原因消失。但是,公正的说在大多数时候是靠谱的,而且可以保证这些脑电波绝对不会在半路上被修改。
为了保证每个脑子好使的人脑子里的每一种货物的价格都是一致的,他们必须要遵照下面这种协议来发送这些脑电波,而且可能要发送很多轮的脑电波才能够完成一次价格的修改。
协议
协议如下:
现在有赵钱孙李王5个脑子好使的人。小赵现在收到了一个毒贩的请求,要将冰毒的价格修改为3块钱。
第一步: 小赵要给冰毒申请一个新的版本号,假设现在的版本号是4,那么他申请到的版本号可能是5。拿到这个版本号之后,他要向其他的脑子好使的人发送脑电波
”小钱:我要修改冰毒的价格,版本号是5。你的价格和版本号是多少?“
”小孙:我要修改冰毒的价格,版本号是5。你的价格和版本号是多少?“
”小李:我要修改冰毒的价格,版本号是5。你的价格和版本号是多少?“
”小王:我要修改冰毒的价格,版本号是5。你的价格和版本号是多少?“
第二步: 在收到上面的脑电波之后,收到的人要开始比较一下自己脑子里的冰毒的版本号和价格。假如自己脑子里的版本号是大于或者等于5,就不用响应这个请求。如果是小于5,那么就把5记住。然后要用脑电波回复这个请求:
例如:
小钱发出脑电波“小赵:我的冰毒的版本号是3,价格是2块钱”
小孙发出脑电波“小赵:我的冰毒的版本号是4,价格是5块钱”
第三步:小赵在如果能在预期的时间内收到2个及以上的回复(2个人加上自己能够构成一个多数派),那么他就可以继续后面的流程。小赵要根据别人的价格、版本号以及自己想要修改的价格来选择一个价格(是的,不一定是他想修改成的3块钱,这个选择比较复杂,先不讲)。然后小赵把这要修改的价格和版本号发给其他的多数派成员。比如在上一步中有小钱、小孙两个人回复了小赵。那么这一次只要发送给小钱、小孙这两个人。
“小钱,我要把冰毒的价格修改成3块钱,版本号是5”
"小孙, 我要把冰毒的价格修改成3块钱,版本号是5"
第四步:在小钱、小孙收到修改价格的脑电波的时候,首先要比较一下自己在第二步记住的版本号,如果是等于5的话。那么就需要回复小赵一条这样的脑电波:
“小赵,我同意版本号为5的冰毒价格修改,你改吧”
第五步:当小赵收到了他出第三步脑电波的所有人的回应之后,他把自己的冰毒价格修改成3块,然后把冰毒改成3块钱的决议发给其他的所有脑子好使的人。
”小钱:冰毒价格修改成3块,版本号是5“
”小孙: 冰毒价格修改成3块,版本号是5 “
”小李: 冰毒价格修改成3块,版本号是5 “
”小王: 冰毒价格修改成3块,版本号是5 “
第六步:所有人收到了这个价格改动成功的消息之后,默默记住。
遗留的问题
现在能够正常走完的协议讲完了,但还是遗留了两个问题:
1 在第三步中讲到了:小赵必须要在其他人的回复中根据别人的价格、版本号以及自己要修改的价格之间选择一个价格。如何进行这个选择呢?
2 这只是正常的能够走完的流程。如果中间除了一些差错导致流程不能走完怎么办?比如在第三步中,小赵收到的回复如果达不到多数派怎么办?第五步,如果小赵不能收到所有的回复怎么办?比如有脑电波丢失了怎么办?
我们先看第二个问题,如果没能走完正常的流程怎么办?办法就是立即继续开始下一轮的协议,一直到协议的六个步骤全部都能走完为止。为什么一定走到某一轮协议之后,一定能够达成协议呢?这也是一个复杂的问题,先不讲,后面再说。从小赵开始第一轮协议到完成最后一轮协议,我们把这些协议合在一起,成为一组协议流程。
回到第一个问题,如何选择一个合适的价格?这个价格是这样进行选择的,在一组协议流程中,小赵选择的这个价格,必须满足:在协议第二步返回的所有价格中(包括自己的价格),一个版本最新的并且版本是大于本组协议的第一轮的版本号的。如果是这一组协议流程的第一轮,可以任意选择价格(当然就选择自己想要改成的那个价格了)。
例如,在一组协议的第三轮,小赵在协议的第三步收到了这些脑电波:
小钱发出脑电波“小赵:我的冰毒的版本号是6,价格是2块钱”
小孙发出脑电波“小赵:我的冰毒的版本号是7,价格是5块钱”
这一轮协议的版本号是8,本来想要改成的价格是3块钱。小赵自己保存的版本号是6,价格是2块钱。这时,小赵需要提出的价格是5块钱。
可是,为什么要加上这样的限制呢? 这又是一个遗留的问题。为了解决这两个遗留的问题,让我们开始做数学题。不过数学题也非常简单,只要认真看,一定能明白。
数学原理
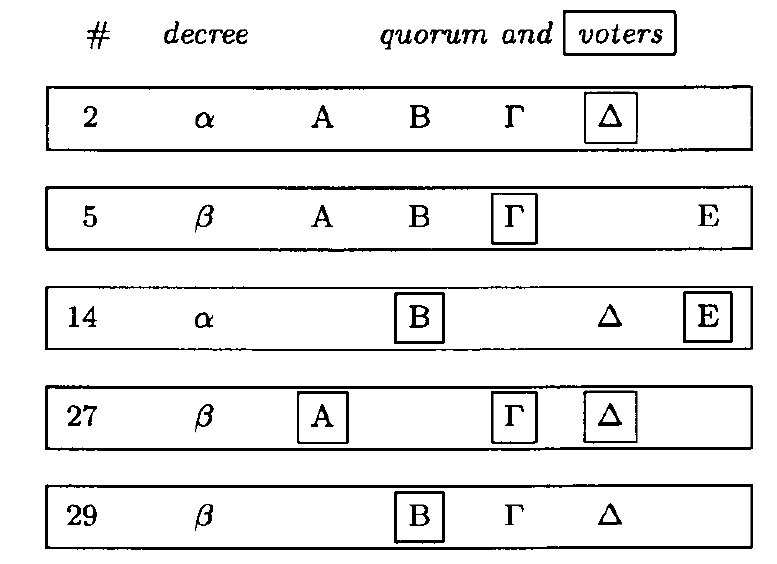
上图是一组协议流程的执行过程。每一行都是一轮协议流程。现在开始我们把一轮协议流程称为投票。上面图中的每一行由这些组成:
第一列: 投票的编号
第二列: 小写字母α β 待表决的决议(例如:某货物价格是3块钱)
其他列 :大写字母是指参与一轮投票的人,也就是投票的代表(例如: 那些脑子好使的人)
每一行都是一轮投票的结果,框中的大写字母是投赞成决议代表。 其余没有框中的表示不赞成的代表。例如第一行, A B Γ是不赞成的,Δ 是赞成的。
我们现在有5个代表,他们是 A B Γ Δ E,有两个决议被需要被表决α 或者 β。
(为什么这些都是希腊字母?因为这种方法是“希腊人”发明的)
每一轮投票都必须要有超过一半的代表参加表决(3个人就是多数了),只有所有参加这一轮表决的代表都赞成这个决议才能被通过。
这样的一组投票有3个基本性质:
1 每一轮的投票都有一个编号或者叫版本号,并且要不断增大
2 任意两轮的投票必须有一个相同的投票代表。
3 每一轮的投票的待表决的决议,必须要等同于参与这一轮的所有的代表的以前投过的赞成票中版本号最大的那一个决议。
这3个性质非常重要,后面一直会用到。前两个性质很简单,看性质3。举例来说:
上面的图中,第一行,投票的编号为2,因为它是这一组投票的第一轮,所以没有代表以前投过赞成票,所以可以任意选一个决议进行表决。
第二行,投票的版本号为5,它的代表A B Γ E 这四个人之前都没有投过赞成票,所以可以任意选一个决议进行表决。
第三行,投票的版本号为14, 它的代表为 B Δ E,这3个人中, Δ 在编号为2的投票中投过α的赞成票,所以这一轮的决议必须为α
第四行,投票的版本号为27,它的代表为 A Γ Δ,这3个人中,A没有投过赞成, Γ在第5轮中投过β的赞成票,Δ在第2轮中投过α的赞成票,所以这一轮的决议必须是β。
类似,第五行的决议必须为β。
因为这一组的投票有这3个基本性质,我们可以推出第一条引理:
引理: 如果满足这3个性质的一组投票,在一组成功的投票之后,所有的投票要进行表决的决议都是这一组成功投票的决议。
证明:因为有一组成功的投票的条件是它的所有的代表都投了赞成票,又因为性质2,任意两轮的投票都有一个相同的代表。所以这一轮 投票的下一组的决议必须等于这一组成功的投票。然后递归可知,后面每一轮投票的决议都相同。
然后可以得到两个定理:
定理1: 如果一组投票中有两组投票成立,那么这两组投票的决议相同。
证明:由引理我们可以知道,如果有一组投票成立,那么后面投票的决议会一直等于这一组成立的投票,所以后面如果有成立的投票,那么也一定等于之前成立的投票的决议。
由这条定理我们可以知道,满足了上面3个性质的一组投票,数据的一致性是有保证的。因为无论投多少次,成立的投票的决议一定是一样的。
定理2:一组投票只要一直投下去,就一定会出现一轮成立的投票。
证明: 反过来看,对于任何一组投票,那么假定有一轮投票,它的所有代表都投赞同票,并且它和之前的投票都有一个代表相同,并且不违背性质3.(这好像没有什么好证明的)
这条定理知道,我们一定会达成一个一致的状态。
回到我们遗留的问题
第一个问题,为什么反复的发起协议就一定能达成一致?
答:看定理2.
第二个问题,为什么在协议的第三步要按照这样的方式选择价格?
“这个价格是这样进行选择的,在一组协议流程中,小赵选择的这个价格,必须满足:在协议第二步返回的所有价格中(包括自己的价格),一个版本最新的并且版本是大于本组协议的第一轮的版本号的。如果是这一组协议流程的第一轮,可以任意选择价格(当然就选择自己想要改成的那个价格了)。”
答:这样的选择,是为了满足性质3
第二个问题,
完