第九章 Caché 算法与数据结构 二叉树

第九章 Caché 算法与数据结构 二叉树

二叉树

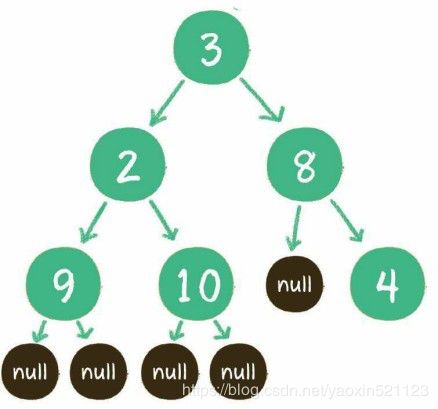
二叉树是树的一种特殊形式。二叉，顾名思义，这种树的每个节点最多有2个孩子节点。注意，这里是最多有2个，也可能只有1个，或者没有孩 子节点。

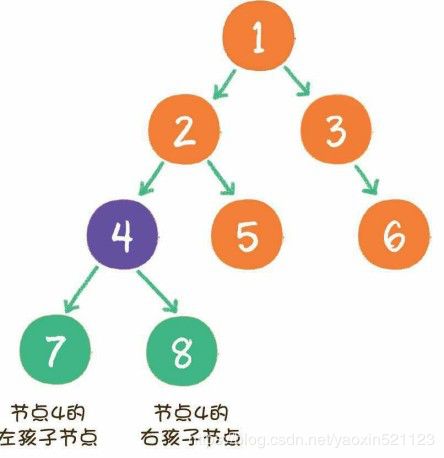
满二叉树

一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。

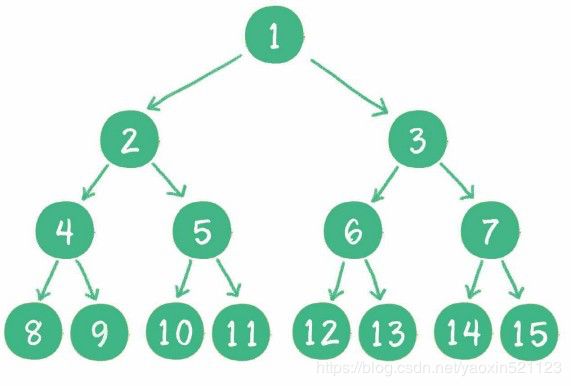
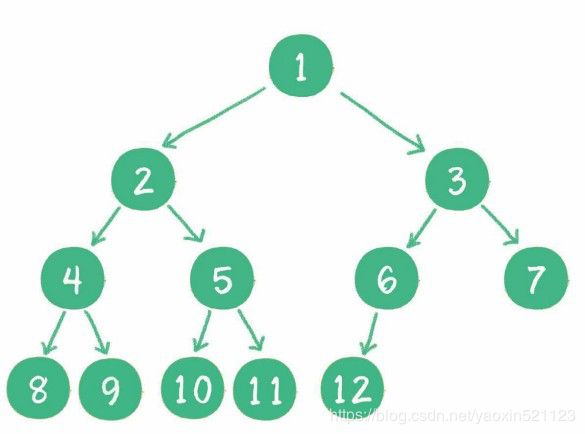
完全二叉树

对一个有n个节点的二叉树，按层级顺序编号，则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同，则这个二叉树为完全二叉树。

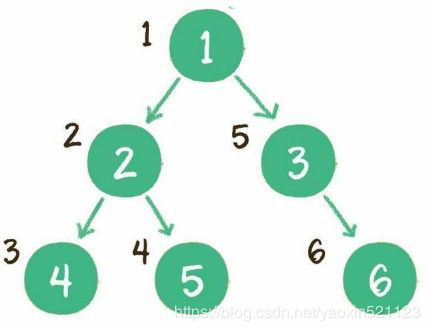
前序遍历

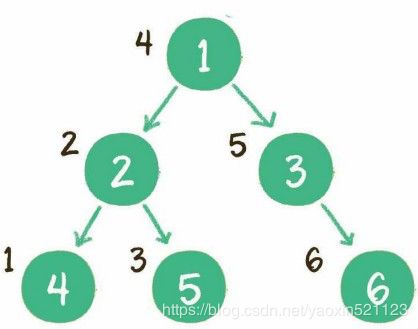
中序遍历

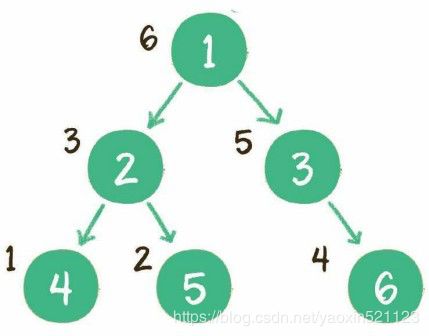
后序遍历

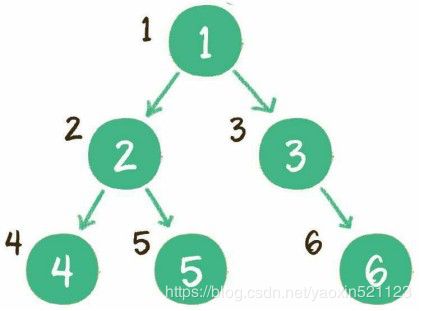
广度遍历

层序遍历，顾名思义，就是二叉树按照从根节点到叶子节点的层次关系，一层一层横向遍历各个节点。

完整实例

构建二叉树

节点类

Class PHA.YX.Arithmetic.BinaryTreeTraversal.Node Extends %RegisteredObject
{

Property leftChild As Node;

Property rightChild As Node;

Property data;

Method %OnNew(data) As %Status [ Private, ServerOnly = 1 ]
{
	s ..data = data
	Quit $$$OK
}

}

二叉树类

Class PHA.YX.Arithmetic.BinaryTreeTraversal Extends %RegisteredObject
{

Property index As %Integer [ InitialExpression = 0 ];

/// 构建二叉树
Method createBinaryTree(inputList As PHA.YX.Arithmetic.LinkedList) As PHA.YX.Arithmetic.BinaryTreeTraversal.Node
{
	#dim node as PHA.YX.Arithmetic.BinaryTreeTraversal.Node = ""
	q:inputList="" ""
	q:inputList.size()=0 ""
	s data = inputList.remove(0)
	s index = 0
	/* 这里的判空很关键。如果元素是空，说明该节点不存在，跳出这一层递归；如果元素非空，继续递归构建该节点的左右孩子。*/
	i data '= "null" d
	.s node = ##class(PHA.YX.Arithmetic.BinaryTreeTraversal.Node).%New(data)
	.s node.leftChild = ..createBinaryTree(inputList)
	.s node.rightChild = ..createBinaryTree(inputList)
	q node
}

/// 二叉树前序遍历
Method preOrderTraversal(node As PHA.YX.Arithmetic.BinaryTreeTraversal.Node)
{
	
	q:node="" ""
	w node.data,!

	d ..preOrderTraversal(node.leftChild)
	d ..preOrderTraversal(node.rightChild)
}

/// 二叉树中序遍历
Method inOrderTraversal(node As PHA.YX.Arithmetic.BinaryTreeTraversal.Node)
{
	q:node="" ""
	
	d ..inOrderTraversal(node.leftChild)
	w node.data,!
	d ..inOrderTraversal(node.rightChild)
}

/// 二叉树后序遍历
Method postOrderTraversal(node As PHA.YX.Arithmetic.BinaryTreeTraversal.Node)
{
	q:node="" ""
	d ..postOrderTraversal(node.leftChild)
	d ..postOrderTraversal(node.rightChild)
	w node.data,!
}

Method levelOrderTraversal(root As PHA.YX.Arithmetic.BinaryTreeTraversal.Node)
{
	#dim queue as PHA.YX.Arithmetic.LinkedQueue = ##class(PHA.YX.Arithmetic.LinkedQueue).%New()
	d queue.addQueue(root)
	while('queue.isEmpty())
	{
		#dim node as PHA.YX.Arithmetic.BinaryTreeTraversal.Node = queue.deleteQueue()
		w node.data,!
		if (node.leftChild'="")
		{
			d queue.addQueue(node.leftChild)
		}
		if (node.rightChild'="")
		{
			d queue.addQueue(node.rightChild)
		}
	}
}

}

调用

/// w ##class(PHA.YX.Arithmetic).BinaryTreeTraversal()
ClassMethod BinaryTreeTraversal()
{
	#dim inputList as PHA.YX.Arithmetic.LinkedList =##class(PHA.YX.Arithmetic.LinkedList).%New()
	d inputList.insert(0,3)
	d inputList.insert(1,2)
	d inputList.insert(2,9)
	d inputList.insert(3,"null")
	d inputList.insert(4,"null")
	d inputList.insert(5,10)
	d inputList.insert(6,"null")
	d inputList.insert(7,"null")
	d inputList.insert(8,8)
	d inputList.insert(9,"null")
	d inputList.insert(10,4)
	//d inputList.output()
	#dim mBinaryTreeTraversal as PHA.YX.Arithmetic.BinaryTreeTraversal = ##class(PHA.YX.Arithmetic.BinaryTreeTraversal).%New()
	#dim treeNode as PHA.YX.Arithmetic.BinaryTreeTraversal.Node = mBinaryTreeTraversal.createBinaryTree(inputList)
	w "前序遍历：",!
	d mBinaryTreeTraversal.preOrderTraversal(treeNode)
	w "中序遍历：",!
	d mBinaryTreeTraversal.inOrderTraversal(treeNode)
	w "后序遍历：",!
	d mBinaryTreeTraversal.postOrderTraversal(treeNode)
	w "广度优先遍历：",!
	d mBinaryTreeTraversal.levelOrderTraversal(treeNode)
	q ""
}

DHC-APP>w ##class(PHA.YX.Arithmetic).BinaryTreeTraversal()
前序遍历：
3
2
9
10
8
4
中序遍历：
9
2
10
3
8
4
后序遍历：
9
10
2
4
8
3
广度优先遍历：
3
2
8
9
10
4