利用R语言如何聚类
利用R语言如何聚类
这篇文章主要介绍几种聚类方法并将其优劣对比,参考《R语言与数据挖掘,最佳实践和经典案例》
本篇文章以让采用鸢尾花数据进行分析.首先要从iris数据集中移除species属性,在下面的代码中,簇的数目设置为3
1、k-means聚类
K-means聚类也称为快速聚类,k-means聚类涉及两个主要方面的问题。:第一,如何测试样本的“亲疏程度”;第二,如何进行聚类。通常,“亲疏程度”的测度有两个角度:第一,数据间的相似程度;第二,数据间的差异程度。衡量相似程度一般可采用简单相关系数或等级相关系数,差异程度一般通过某种距离来测度。k-means聚类方法采用第二个测度角度。k-means聚类的基本思想是先将样本空间分割成随意的若干类,然后计算所有样本点到各类中的距离,由于初始聚类结果是在空间随意分割的基础上产生的,因此无法确保所给出的聚类解满足上述要求,所以要经过多次反复。聚类数目确定本身并不简单,太大或太小都会失去聚类的意义。由于距离是k-means聚类的基础,因此也要注意:1、当聚类变量值有数量级上的差异时,一般通过标准化处理消除变量的数量级差异。2、聚类变量之间不应该有较强的线性相关关系。
iris2 <- iris
iris2$Species <- NULL
kmeans.result <- kmeans(iris2, 3)
将聚类结果与species进行比较
table(iris$Species,kmeans.result$cluster)
1 2 3
setosa 0 50 0
versicolor 48 0 2
virginica 14 0 36
绘制所有簇以及簇中心,值得注意的是多次运行得到的k-means聚类结果可能不同,因为初始的簇中心是随机选择的
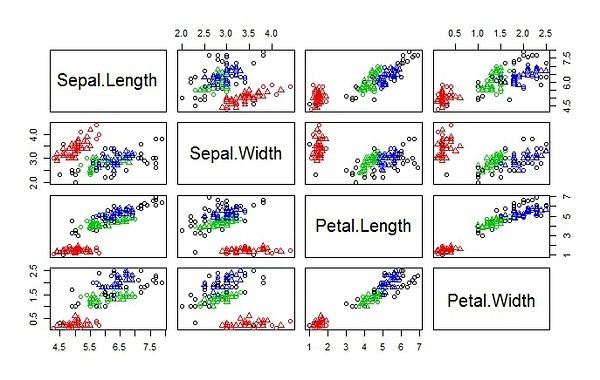
plot(iris2[c("Sepal.Length", "Sepal.Width")], col = kmeans.result$cluster)
points(kmeans.result$centers[,c("Sepal.Length", "Sepal.Width")], col = 1:3, pch = 8, cex=2)
2、k-medoids聚类
又被称为K-中心点聚类。函数pam()和pamk()都可以进行k-medoids聚类,k-medoids聚类与k-means聚类类似,主要区别是k-means聚类选择簇中心表示聚类簇,而k-medoids聚类选择靠近簇中心的对象表示聚类簇,在含有离群点的情况下,k-medoids聚类的鲁棒性更好,不像k-means聚类容易受极值影响。
library(fpc)
iris2 <- iris
iris2$Species <- NULL
pamk.result <- pamk(iris2)
pamk.result$nc #簇个数
[1] 2
table(pamk.result$pamobject$clustering, iris$Species)
setosa versicolor virginica
1 50 1 0
2 0 49 50
plot(iris2[c("Sepal.Length", "Sepal.Width")], col = pamk.result$pamobject$clustering)
points(pamk.result$pamobject$medoids[,c("Sepal.Length", "Sepal.Width")], col = 1:3, pch = 8, cex=2)
图中可以看到聚类分为两簇,这是因为pamk()函数会调用pam()函数或clara()函数根据最优平均阴影官渡估计的聚类簇个数来划分数据。
layout(matrix(c(1,2),1,2)) # 每页两张图
plot(pamk.result$pamobject)
layout(matrix(1)) #改回每页一张图
上图右边的图像显示了两个簇的阴影,当si的值较大时(接近1)表明相应的观测点能够正确的划分到相似性较大的簇中,从上面的例子我们可以看出两个簇的si均值分别为0.81和0.62.划分结果很好。
接下来使用函数pam(),并设置k=3.
library(cluster)
pam.result <- pam(iris2, 3)
table(pam.result$clustering, iris$Species)
setosa versicolor virginica
1 50 0 0
2 0 48 14
3 0 2 36
layout(matrix(c(1,2),1,2)) # 每页两张图
plot(pam.result)
layout(matrix(1)) #改回每页一张图
从上面看似乎函数pam()得到的聚类结果更好,因为pam()人工设置识别出三个不同的簇,而pamk()则是利用启发方法识别簇个数。所以很难说谁好谁坏。
3.层次聚类
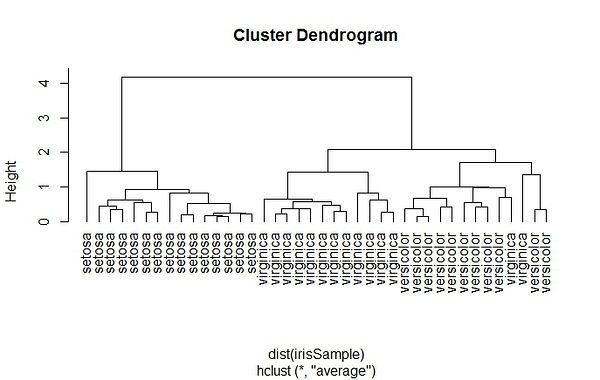
层次聚类是另一种主要的聚类方法,也被称为系统聚类,它具有一些十分必要的特性使得它成为广泛应用的聚类方法。层次聚类的主要思想是:首先每个观测点自成一类;然后,度量所有的观测点彼此间的紧密程度,将其中最亲密的观测点聚成一个小类,形成n-1类,接下来再次度量剩余的观测点和小类间的亲密程度,并用当前最亲密的观测点或小类聚成一类;重复上述过程,不断将观测点与小类聚成大类。层次聚类也可以理解为生成一系列嵌套的聚类树来完成聚类。单点聚类处在树的最底层,在树的顶层有一个根节点聚类。根节点聚类覆盖了全部的所有数据点。首先,我们随机抽取一个40条记录的样本,与之前相同,从数据样本中剔除species属性。
idx <- sample(1:dim(iris)[1], 40)
irisSample <- iris[idx,]
irisSample$Species <- NULL
hc <- hclust(dist(irisSample), method="ave")
plot(hc, hang = -1, labels=iris$Species[idx])
# 修剪树使之分为3类
rect.hclust(hc, k=3)
groups <- cutree(hc, k=3)
4.基于密度的聚类
基于密度的聚类优势在于可以返现任意形状的簇,并且对噪声数据不敏感,相比之下,k-means算法更倾向于发现球状的且大小相近的簇,这里我们用到的是DBSCAN算法,还有OPTICS算法以及.DENCLUE算法,这两个算法我也在学习当中,下面以DBSCAN算法为例,说明其算法思想,首先明确其输入值为待聚类数据集,半径E与亲密度阀值MinPts(假设取3):
1.从数据集当中选择一个未处理的样本P,以这个样本为中心,半径E做圆,如果圈入点个数为3,满足阀值MinPts,将圈内4个点形成一个簇,称该对象为核心对象。圈内的3个点与该对象P为直接密度可达,标记为类1同样的道理考察其他样本点,递归该对象P直接密度可达的所有对象代替P回到第一步。
2.如果圈入点个数为2,不满足阀值MinPts,将其设定为边界对象,然后继续考察其他点。如果还有没被标记的对象,则从中任选一个作为p,回到第一步。当所有的点都被考察后,这个过程就结束了。
3.最后一步将各点归类,类中的所有对象都是密度相连的。得到一个类后,同样我们可以得到另一个类
优点:
1. 对噪声不敏感。
2. 能发现任意形状的聚类。
缺点:
1. 聚类的结果与参数有很大的关系。
2. DBSCAN用固定参数识别聚类,但当聚类的稀疏程度不同时,相同的判定标准可能会破坏聚类的自然结构,即较稀的聚类会被划分为多个类或密度较大且离得较近的类会被合并成一个聚类
library(fpc)
iris2 <- iris[-5] # 与之前相同,从数据样本中剔除species属性
ds <- dbscan(iris2, eps=0.42, MinPts=5)
# compare clusters with original class labels
table(ds$cluster, iris$Species)
setosa versicolor virginica
0 2 10 17
1 48 0 0
2 0 37 0
3 0 3 33
上面的数据表中1到3为识别出来的3个聚类簇,0表示噪声数据或利群点,即不属于任何簇的对象。
plot(ds, iris2)
plot(ds, iris2[c(1,4)])
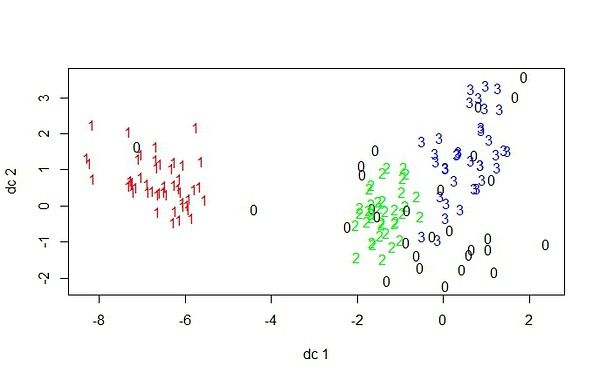
fpc包还提供了另一个展示聚类分析的函数plotcluster(),值得一提的是,数据将被投影到不同的簇中
plotcluster(iris2, ds$cluster)
5基于模型的聚类——EM算法
EM算法也成为期望最大化算法,在是使用该算法聚类时,将数据集看作一个有隐形变量的概率模型,并实现模型最优化,即获取与数据本身性质最契合的聚类方式为目的,通过‘反复估计’模型参数找出最优解,同时给出相应的最有类别级数k。
> library('mclust')
> EM<-Mclust(iris[,-5])
> summary(EM,parameters=T)
----------------------------------------------------
Gaussian finite mixture model fitted by EM algorithm
----------------------------------------------------
Mclust VEV (ellipsoidal, equal shape) model with 2 components:
log.likelihood n df BIC ICL
-215.726 150 26 -561.7285 -561.7289
Clustering table:
1 2
50 100
Mixing probabilities:
1 2
0.333332 0.666668
Means:
[,1] [,2]
Sepal.Length 5.0060021 6.261996
Sepal.Width 3.4280046 2.871999
Petal.Length 1.4620006 4.905993
Petal.Width 0.2459998 1.675997
Variances:
[,,1]
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 0.15065097 0.13080108 0.020844624 0.013091029
Sepal.Width 0.13080108 0.17604544 0.016032479 0.012214539
Petal.Length 0.02084462 0.01603248 0.028082603 0.006015675
Petal.Width 0.01309103 0.01221454 0.006015675 0.010423651
[,,2]
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 0.4000437 0.10865439 0.3994013 0.14368238
Sepal.Width 0.1086544 0.10928074 0.1238902 0.07284378
Petal.Length 0.3994013 0.12389025 0.6109012 0.25738947
Petal.Width 0.1436824 0.07284378 0.2573895 0.16808166
我们可以看到最优类别级数为2,各类分别含有50,100
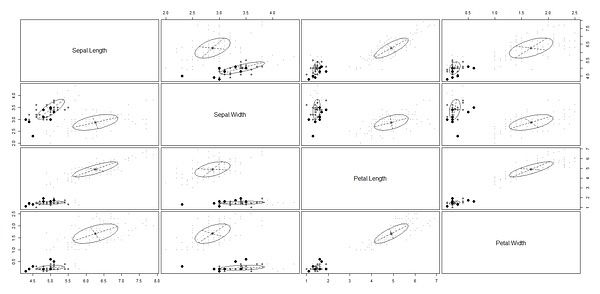
plot(EM,what='classification')
值得一提的是clustMD()包也是可以实现基于模型的聚类——EM算法的,而且对数据集包含离散变量、连续变量、二进制变量、有序变量甚至是NA值都可以成功聚类。
本文提到的算法只是聚类算法中的一小部分,未来会不断更新。
另外 这篇文章中提到一些聚类方法的比较,非常值得学习
本篇文章以让采用鸢尾花数据进行分析.首先要从iris数据集中移除species属性,在下面的代码中,簇的数目设置为3
1、k-means聚类
K-means聚类也称为快速聚类,k-means聚类涉及两个主要方面的问题。:第一,如何测试样本的“亲疏程度”;第二,如何进行聚类。通常,“亲疏程度”的测度有两个角度:第一,数据间的相似程度;第二,数据间的差异程度。衡量相似程度一般可采用简单相关系数或等级相关系数,差异程度一般通过某种距离来测度。k-means聚类方法采用第二个测度角度。k-means聚类的基本思想是先将样本空间分割成随意的若干类,然后计算所有样本点到各类中的距离,由于初始聚类结果是在空间随意分割的基础上产生的,因此无法确保所给出的聚类解满足上述要求,所以要经过多次反复。聚类数目确定本身并不简单,太大或太小都会失去聚类的意义。由于距离是k-means聚类的基础,因此也要注意:1、当聚类变量值有数量级上的差异时,一般通过标准化处理消除变量的数量级差异。2、聚类变量之间不应该有较强的线性相关关系。
iris2 <- iris
iris2$Species <- NULL
kmeans.result <- kmeans(iris2, 3)
将聚类结果与species进行比较
table(iris$Species,kmeans.result$cluster)
1 2 3
setosa 0 50 0
versicolor 48 0 2
virginica 14 0 36
绘制所有簇以及簇中心,值得注意的是多次运行得到的k-means聚类结果可能不同,因为初始的簇中心是随机选择的
plot(iris2[c("Sepal.Length", "Sepal.Width")], col = kmeans.result$cluster)
points(kmeans.result$centers[,c("Sepal.Length", "Sepal.Width")], col = 1:3, pch = 8, cex=2)
2、k-medoids聚类
又被称为K-中心点聚类。函数pam()和pamk()都可以进行k-medoids聚类,k-medoids聚类与k-means聚类类似,主要区别是k-means聚类选择簇中心表示聚类簇,而k-medoids聚类选择靠近簇中心的对象表示聚类簇,在含有离群点的情况下,k-medoids聚类的鲁棒性更好,不像k-means聚类容易受极值影响。
library(fpc)
iris2 <- iris
iris2$Species <- NULL
pamk.result <- pamk(iris2)
pamk.result$nc #簇个数
[1] 2
table(pamk.result$pamobject$clustering, iris$Species)
setosa versicolor virginica
1 50 1 0
2 0 49 50
plot(iris2[c("Sepal.Length", "Sepal.Width")], col = pamk.result$pamobject$clustering)
points(pamk.result$pamobject$medoids[,c("Sepal.Length", "Sepal.Width")], col = 1:3, pch = 8, cex=2)
图中可以看到聚类分为两簇,这是因为pamk()函数会调用pam()函数或clara()函数根据最优平均阴影官渡估计的聚类簇个数来划分数据。
layout(matrix(c(1,2),1,2)) # 每页两张图
plot(pamk.result$pamobject)
layout(matrix(1)) #改回每页一张图
上图右边的图像显示了两个簇的阴影,当si的值较大时(接近1)表明相应的观测点能够正确的划分到相似性较大的簇中,从上面的例子我们可以看出两个簇的si均值分别为0.81和0.62.划分结果很好。
接下来使用函数pam(),并设置k=3.
library(cluster)
pam.result <- pam(iris2, 3)
table(pam.result$clustering, iris$Species)
setosa versicolor virginica
1 50 0 0
2 0 48 14
3 0 2 36
layout(matrix(c(1,2),1,2)) # 每页两张图
plot(pam.result)
layout(matrix(1)) #改回每页一张图
从上面看似乎函数pam()得到的聚类结果更好,因为pam()人工设置识别出三个不同的簇,而pamk()则是利用启发方法识别簇个数。所以很难说谁好谁坏。
3.层次聚类
层次聚类是另一种主要的聚类方法,也被称为系统聚类,它具有一些十分必要的特性使得它成为广泛应用的聚类方法。层次聚类的主要思想是:首先每个观测点自成一类;然后,度量所有的观测点彼此间的紧密程度,将其中最亲密的观测点聚成一个小类,形成n-1类,接下来再次度量剩余的观测点和小类间的亲密程度,并用当前最亲密的观测点或小类聚成一类;重复上述过程,不断将观测点与小类聚成大类。层次聚类也可以理解为生成一系列嵌套的聚类树来完成聚类。单点聚类处在树的最底层,在树的顶层有一个根节点聚类。根节点聚类覆盖了全部的所有数据点。首先,我们随机抽取一个40条记录的样本,与之前相同,从数据样本中剔除species属性。
idx <- sample(1:dim(iris)[1], 40)
irisSample <- iris[idx,]
irisSample$Species <- NULL
hc <- hclust(dist(irisSample), method="ave")
plot(hc, hang = -1, labels=iris$Species[idx])
# 修剪树使之分为3类
rect.hclust(hc, k=3)
groups <- cutree(hc, k=3)
4.基于密度的聚类
基于密度的聚类优势在于可以返现任意形状的簇,并且对噪声数据不敏感,相比之下,k-means算法更倾向于发现球状的且大小相近的簇,这里我们用到的是DBSCAN算法,还有OPTICS算法以及.DENCLUE算法,这两个算法我也在学习当中,下面以DBSCAN算法为例,说明其算法思想,首先明确其输入值为待聚类数据集,半径E与亲密度阀值MinPts(假设取3):
1.从数据集当中选择一个未处理的样本P,以这个样本为中心,半径E做圆,如果圈入点个数为3,满足阀值MinPts,将圈内4个点形成一个簇,称该对象为核心对象。圈内的3个点与该对象P为直接密度可达,标记为类1同样的道理考察其他样本点,递归该对象P直接密度可达的所有对象代替P回到第一步。
2.如果圈入点个数为2,不满足阀值MinPts,将其设定为边界对象,然后继续考察其他点。如果还有没被标记的对象,则从中任选一个作为p,回到第一步。当所有的点都被考察后,这个过程就结束了。
3.最后一步将各点归类,类中的所有对象都是密度相连的。得到一个类后,同样我们可以得到另一个类
优点:
1. 对噪声不敏感。
2. 能发现任意形状的聚类。
缺点:
1. 聚类的结果与参数有很大的关系。
2. DBSCAN用固定参数识别聚类,但当聚类的稀疏程度不同时,相同的判定标准可能会破坏聚类的自然结构,即较稀的聚类会被划分为多个类或密度较大且离得较近的类会被合并成一个聚类
library(fpc)
iris2 <- iris[-5] # 与之前相同,从数据样本中剔除species属性
ds <- dbscan(iris2, eps=0.42, MinPts=5)
# compare clusters with original class labels
table(ds$cluster, iris$Species)
setosa versicolor virginica
0 2 10 17
1 48 0 0
2 0 37 0
3 0 3 33
上面的数据表中1到3为识别出来的3个聚类簇,0表示噪声数据或利群点,即不属于任何簇的对象。
plot(ds, iris2)
plot(ds, iris2[c(1,4)])
fpc包还提供了另一个展示聚类分析的函数plotcluster(),值得一提的是,数据将被投影到不同的簇中
plotcluster(iris2, ds$cluster)
5基于模型的聚类——EM算法
EM算法也成为期望最大化算法,在是使用该算法聚类时,将数据集看作一个有隐形变量的概率模型,并实现模型最优化,即获取与数据本身性质最契合的聚类方式为目的,通过‘反复估计’模型参数找出最优解,同时给出相应的最有类别级数k。
> library('mclust')
> EM<-Mclust(iris[,-5])
> summary(EM,parameters=T)
----------------------------------------------------
Gaussian finite mixture model fitted by EM algorithm
----------------------------------------------------
Mclust VEV (ellipsoidal, equal shape) model with 2 components:
log.likelihood n df BIC ICL
-215.726 150 26 -561.7285 -561.7289
Clustering table:
1 2
50 100
Mixing probabilities:
1 2
0.333332 0.666668
Means:
[,1] [,2]
Sepal.Length 5.0060021 6.261996
Sepal.Width 3.4280046 2.871999
Petal.Length 1.4620006 4.905993
Petal.Width 0.2459998 1.675997
Variances:
[,,1]
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 0.15065097 0.13080108 0.020844624 0.013091029
Sepal.Width 0.13080108 0.17604544 0.016032479 0.012214539
Petal.Length 0.02084462 0.01603248 0.028082603 0.006015675
Petal.Width 0.01309103 0.01221454 0.006015675 0.010423651
[,,2]
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 0.4000437 0.10865439 0.3994013 0.14368238
Sepal.Width 0.1086544 0.10928074 0.1238902 0.07284378
Petal.Length 0.3994013 0.12389025 0.6109012 0.25738947
Petal.Width 0.1436824 0.07284378 0.2573895 0.16808166
我们可以看到最优类别级数为2,各类分别含有50,100
plot(EM,what='classification')
值得一提的是clustMD()包也是可以实现基于模型的聚类——EM算法的,而且对数据集包含离散变量、连续变量、二进制变量、有序变量甚至是NA值都可以成功聚类。
本文提到的算法只是聚类算法中的一小部分,未来会不断更新。
另外 这篇文章中提到一些聚类方法的比较,非常值得学习