贪心算法之哈夫曼编码
目录
- 哈夫曼编码简介
- 举例以及详细说明
- 代码块
- 测试结果
哈夫曼编码简介
二叉树中有一种特别的树——哈夫曼树(最优二叉树),其通过某种规则(权值)来构造出一哈夫曼二叉树,在这个二叉树中,只有叶子节点才是有效的数据节点(很重要),其他的非叶子节点是为了构造出哈夫曼而引入的!
哈夫曼编码是一个通过哈夫曼树进行的一种编码,一般情况下,以字符:‘0’与‘1’表示。编码的实现过程很简单,只要实现哈夫曼树,通过遍历哈夫曼树,规定向左子树遍历一个节点编码为“0”,向右遍历一个节点编码为“1”,结束条件就是遍历到叶子节点!因为上面说过:哈夫曼树叶子节点才是有效数据节点!
举例以及详细说明
一、对给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,…,Ti,…,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。(为方便在计算机上实现算 法,一般还要求以Ti的权值Wi的升序排列。)
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步,直到集合F中只有一棵二叉树为止。
简易的理解就是,假如我有A,B,C,D,E五个字符,出现的频率(即权值)分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树,即取1,2构成新树,其结点为1+2=3,如图:

虚线为新生成的结点,第二步再把新生成的权值为3的结点放到剩下的集合中,所以集合变成{5,4,3,3},再根据第二步,取最小的两个权值构成新树,如图:

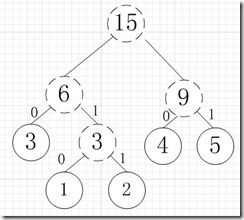
所以各字符对应的编码为:A->11,B->10,C->00,D->011,E->010
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩,加密解密等场合。
代码块
#include