分块算法介绍(分块入门练习-1)
前言
之前只了解分块,但没有深入学习.但之前集训时遇到http://codeforces.com/gym/100960/problem/G,当时现场树状数组没有调出来,赛后写出后上网搜其他方法,发现了一个奇妙的分块方法,便决定抽空深入学习一下这种优化的暴力——分块.
关键名词:
- 区间：一段连续子序列
- 区间操作：对某个区间进行同类型相同规模的操作
- 块：将一个数列划分为连续的块分块算法一般保证前
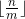块大小均为
,最后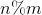
个元素单独为一个块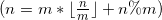
- 整块：在一个区间操作时，完整包含于区间的块
- 不完整的块：在一个区间操作时，只有部分包含于区间的块，即区间左右端点所在的两个块
- 即处理一个区间时,根据之前分好的块可以分为 不完整-完整-不完整 三块进行处理,
- 一般会对完整区块维护一定的属性如:区间加
![=>tag[x]](http://img.e-com-net.com/image/info8/29db8a2ab4ed4e89891f3d66f2a7cb78.gif)
, 区间排序后的序列![=>val\_\ blg[which\_\ block][size]](http://img.e-com-net.com/image/info8/32a557b4041a4ac98474eb10dcec039a.gif)
等
变量说明:
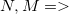数列大小,操作数(包括修改与询问)![blg[i],block=>](http://img.e-com-net.com/image/info8/c7ca86a194184fae83bc43c6ae56e948.gif)
第
个元素所属区间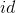
,块的大小(描述了序列与块之间的联系)![val[i],tag[block\_id]=>](http://img.e-com-net.com/image/info8/de95ec8fb0ab4a1c805afddd362ca3df.gif)
第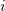
个元素的值,第
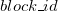个区间维护的属性(这里用最常见的
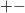操作作为代表)
练习 分块九题
题解 练习-2 练习-3
入门题-1
给出一个长为 
的数列，以及 个操作，操作涉及区间加法，单点查值。
数据范围:
一道经典的支持区间操作的数据结构的模板题.
分块的处理则是将涉及的每个整块进行打包(利用![tag[]](http://img.e-com-net.com/image/info8/072c44c41baa4fcab089759c2b791721.gif){kind=small}
),从而进行优化
设每个块的大小为
,则每次区间操作涉及 不完整-完整-不完整 三个部分耗费的时间为
,
表示枚举的消耗,
表示打包处理一个块的消耗
而
,所以最坏情况下每次操作耗费时间粗略记为
,一般认为渐近意义上
相同,所以一般块大小
比较合适(根据不同题目可选择不同的块,在渐近意义下是较优的,可以在调试过程中调整块大小比较时间以近一步优化时间常数)
针对本题,一个元素最终值为![val[i]+tag[blg[i]]](http://img.e-com-net.com/image/info8/a35b55706c054bd680f782ca0513a7a2.gif){kind=small}
,涉及的分块主要在于区间加操作,时间复杂度为
#include
#include
#include
#include
#include
using namespace std;
using LL = long long;
LL getint();
int N, M;
LL block, val[500005], blg[500005], tag[1005];
void add(int l, int r, int key);
int main(){
N = getint(), block = sqrt(N);
int i;
for(i = 1; i <= N; i++)
val[i] = getint();
for(i = 1; i <= N; i++)
blg[i] = (i - 1) / block + 1;
for(i = 1; i <= N; i++){
int op, x, y, key;
op = getint(), x = getint();
y = getint(), key = getint();
if(op == 0){
add(x, y, key);
}else
printf("%lld\n", val[y] + tag[blg[y]]);
}
return 0;
}
void add(int l, int r, int key){
int i, top;
for(i = l, top = min(blg[l] * block, 1LL * r); i <= top; i++)
val[i] += key;
if(blg[l] != blg[r])
for(i = (blg[r] - 1) * block + 1; i <= r; i++)
val[i] += key;
for(i = blg[l] + 1; i <= blg[r] - 1; i++)
tag[i] += key;
}
LL getint(){
LL res = 0, mark = 1;
char ch = getchar();
while(ch<'0' || ch>'9'){
if(ch == '-') mark = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
res = 10 * res + ch - '0', ch = getchar();
return mark * res;
}
入门题-2
给出一个长为n的数列，以及n个操作，操作涉及区间加法，询问区间内小于某个值x的元素个数。
数据范围:
有了上一题的分析,可以看出,分块其实是优化的暴力,其通过维护一段区间的某个属性进而优化时间
于是在进行选择分块策略时,主要解决以下几个问题:
- 针对不完整块如何进行处理?
- 完整的块如何进行处理?
- 需要对每个块维护哪些信息?如何进行预处理?
- 如何合并答案?
针对这一题,考虑对每个块维护2个属性![tag[],val\_blg[]](http://img.e-com-net.com/image/info8/e8152f9d08f049509963d62e3581a8e6.gif){kind=small}
,维护区间加与该区间排序后的序列(针对![val[]](http://img.e-com-net.com/image/info8/22b3fecccb1a4023a009748301b91401.gif){kind=small}
排序)
首先考虑
操作,对于不完整的块进行枚举而完整的块进行二分查找即可,时间
对于
操作,完整的块仅维护即可,而不完整的块枚举维护后对该块进行重新排序即可,时间
可以看出取不一定最优,但可以在渐近意义上逼近最优的值,故一般默认(不同题目会调整大小优化常数).
#include
#include
#include
#include
#include
#include
using namespace std;
using LL = long long;
int N;
LL block, val[50005], blg[50005], tag[1005];
vector val_blg[1005];
void add(int, int, int);
int query(int, int, int);
int main(){
ios::sync_with_stdio(false);
cin >> N, block = sqrt(N);
int i;
for(i = 1; i <= N; i++)
cin >> val[i];
for(i = 1; i <= N; i++)
blg[i] = (i - 1) / block + 1, val_blg[blg[i]].push_back(val[i]);
for(i = 1; i <= blg[N]; i++)
sort(val_blg[i].begin(), val_blg[i].end());
for(i = 1; i <= N; i++){
int op, x, y, key;
cin >> op >> x >> y >> key;
if(op == 0) add(x, y, key);
else cout << query(x, y, key * key) << endl;
}
return 0;
}
void reset(int block_id);
void add(int l, int r, int key){
int i, top;
for(i = l, top = min(blg[l] * block, 1LL * r); i <= top; i++)
val[i] += key;
reset(blg[l]);
if(blg[l] != blg[r]){
for(i = (blg[r] - 1) * block + 1; i <= r; i++)
val[i] += key;
reset(blg[r]);
}
for(i = blg[l] + 1; i <= blg[r] - 1; i++)
tag[i] += key;
}
int query(int l, int r, int key){
int i, top, res = 0;
for(i = l, top = min(blg[l] * block, 1LL * r); i <= top; i++)
if(val[i] + tag[blg[i]] < key) res++;
if(blg[l] != blg[r])
for(i = (blg[r] - 1) * block + 1; i <= r; i++)
if(val[i] + tag[blg[i]] < key) res++;
for(i = blg[l] + 1; i <= blg[r] - 1; i++)
res += lower_bound(val_blg[i].begin(), val_blg[i].end(), key - tag[i]) - val_blg[i].begin();
return res;
}
void reset(int x){
int i, top;
val_blg[x].clear();
for(i = (x - 1) * block + 1, top = min(x * block, 1LL * N); i <= top; i++)
val_blg[x].push_back(val[i]);
sort(val_blg[x].begin(), val_blg[x].end());
}
入门题-3
给出一个长为n的数列，以及n个操作，操作涉及区间加法，询问区间内小于某个值x的前驱（比其小的最大元素）。
数据范围:
上述第二题的一种变式,一样的数据结构的扩张,在操作时先枚举每个块(包括完整与不完整)的
的前驱,在整合比较得到答案
也可以使用set维护
#include
#include
#include
#include
#include
#include
using namespace std;
using LL = long long;
int N;
LL block, val[100005], blg[100005], tag[1205];
vector val_blg[1205];
void add(int l, int r, int key);
LL query(int l, int r, int key);
int main(){
ios::sync_with_stdio(false);
int i;
cin >> N, block = sqrt(N);
for(i = 1; i <= N; i++) cin >> val[i];
for(i = 1; i <= N; i++){
blg[i] = (i - 1) / block + 1;
val_blg[blg[i]].push_back(val[i]);
}
for(i = 1; i <= blg[N]; i++)
sort(val_blg[i].begin(), val_blg[i].end());
for(i = 1; i <= N; i++){
int op, x, y, key;
cin >> op >> x >> y >> key;
if(op == 0) add(x, y, key);
else cout << query(x, y, key) << endl;
}
return 0;
}
void reset(int blg_id);
void add(int l, int r, int key){
int i, top;
for(i = l, top = min(blg[l] * block, 1LL * r); i <= top; i++)
val[i] += key;
reset(blg[l]);
if(blg[l] != blg[r]){
for(i = (blg[r] - 1) * block + 1; i <= r; i++)
val[i] += key;
reset(blg[r]);
}
for(i = blg[l] + 1; i <= blg[r] - 1; i++)
tag[i] += key;
}
LL query(int l, int r, int key){
int i, top, x;
vector tmp;
for(i = l, top = min(blg[l] * block, 1LL * r), x = -1; i <= top; i++)
if(val[i] + tag[blg[i]] < key && x < val[i] + tag[blg[i]])
x = val[i] + tag[blg[i]];
if(x != -1) tmp.push_back(x);
if(blg[l] != blg[r]){
for(i = (blg[r] - 1) * block + 1, x = -1; i <= r; i++)
if(val[i] + tag[blg[i]] < key && x < val[i] + tag[blg[i]])
x = val[i] + tag[blg[i]];
if(x != -1) tmp.push_back(x);
}
for(i = blg[l] + 1; i <= blg[r] - 1; i++){
int ind;
ind = lower_bound(val_blg[i].begin(), val_blg[i].end(), key - tag[i]) - val_blg[i].begin();
if(ind && val_blg[i][ind - 1] + tag[i] < key)
tmp.push_back(val_blg[i][ind - 1] + tag[i]);
}
if(!tmp.size()) return -1;
sort(tmp.begin(), tmp.end());
int ind = lower_bound(tmp.begin(), tmp.end(), key) - tmp.begin();
return tmp[ind - 1];
}
void reset(int x){
int i, top;
val_blg[x].clear();
for(i = (x - 1) * block + 1, top = min(x * block, 1LL * N); i <= top; i++)
val_blg[x].push_back(val[i]);
sort(val_blg[x].begin(), val_blg[x].end());
}
#include
#include
#include
#include
#include
#include
#include
using namespace std;
using LL = long long;
LL N;
LL block, val[100005], blg[100005], tag[1205];
set S[1205];
void add(int, int, int);
LL query(int, int, int);
int main(){
ios::sync_with_stdio(false);
int i;
cin >> N, block = sqrt(N);
for(i = 1; i <= N; i++) cin >> val[i];
for(i = 1; i <= N; i++){
blg[i] = (i - 1) / block + 1;
S[blg[i]].insert(val[i]);
}
for(i = 1; i <= N; i++){
int op, x, y, key;
cin >> op >> x >> y >> key;
if(op == 0) add(x, y, key);
else cout << query(x, y, key) << endl;
}
return 0;
}
void add(int l, int r, int key){
int i, top;
for(i = l, top = min(blg[l] * block, 1LL * r); i <= top; i++){
S[blg[i]].erase(val[i]);
val[i] += key;
S[blg[i]].insert(val[i]);
}
if(blg[l] != blg[r])
for(i = (blg[r] - 1) * block + 1; i <= r; i++){
S[blg[i]].erase(val[i]);
val[i] += key;
S[blg[i]].insert(val[i]);
}
for(i = blg[l] + 1; i <= blg[r] - 1; i++)
tag[i] += key;
}
LL query(int l, int r, int key){
LL res = -1;
int i, top;
for(i = l, top = min(blg[l] * block, 1LL * r); i <= top; i++)
if(val[i] + tag[blg[i]] < key) res = max(res, val[i] + tag[blg[i]]);
if(blg[l] != blg[r])
for(i = (blg[r] - 1) * block + 1; i <= r; i++)
if(val[i] + tag[blg[i]] < key) res = max(res, val[i] + tag[blg[i]]);
for(i = blg[l] + 1; i <= blg[r] - 1; i++){
auto it = S[i].lower_bound(key - tag[i]);
if(it == S[i].begin()) continue;
it--;
res = max(res, *it + tag[i]);
}
return res;
}