动态规划之01背包问题(一)

动态规划之01背包问题(一)

背包问题是动态规划最经典的问题之一，这篇博客会初步探索背包问题，在后续系列会继续深入。

问题介绍

有n个物品，价值和重量分别为vi和wi,背包承重W，求装入背包的最大价值。
例子：
n=4
w={2,1,3,2}
v={2,2,4,3}
W=5
输出
V=7(选择第0，1，3件物品或者第2，3件物品)

直观思维

情况1 在背包还放得下这件物品时，选与不选都试一下，选二者的较大值
情况2 在背包放不下这件物品的时候，直接跳过这件物品
情况3 没有物品可选

例如上例
物品1：我们先看第一个物品 w=2，v=2,W可用为5，此时是情况1，
也就是说此时要选择max(放第一件物品，不放第一件物品)

物品2：再看第二个物品，因为物品有两种情况，放第一件物品与不放，所以第二件物品要分情况讨论。
当不放第一件物品时，第二个物品 w=1 , v=2,W可用为5，此时是情况1，
也就是说此时要选择max(放第二件物品，不放第二件物品)
当放第一件物品时，第二个物品 w=1,v=2,W可用为5-2=3，此时是情况1，
也就是说此时要选择max(放第二件物品，不放第二件物品)
物品3：以此类推，类似像树形展开。如下图所示：
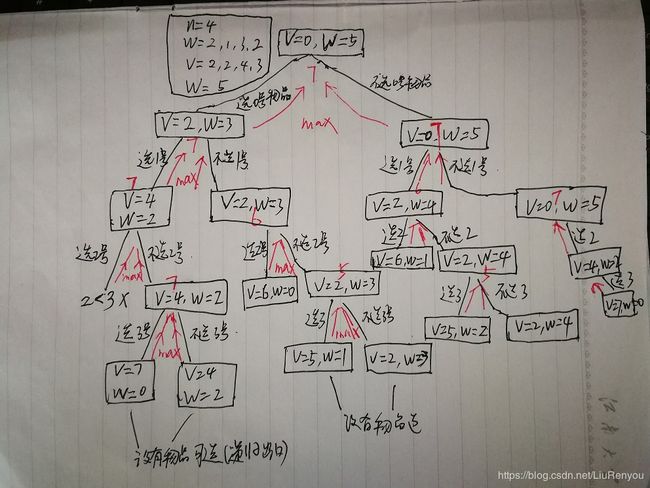红色字体是递归出口向上一层一层返回。

普通递归

基于以上分析，不难想到利用递归来解决这个问题。既然利用递归，那么就要想好递归函数是否需要返回值，参数类型，递归条件，递归出口。

返回值：明显要返回int。
参数类型：我们需要从第一个物品搜索到最后一和物品，所以参数肯定要一个数组的下标i（从0开始）表示当前在选择的物品，我们还需要知道当前背包还剩余的体积是多少，所以需要一个参数j来表示它，很明显i的初始调用值为0，j的初始调用值为W.
递归条件：
情况1：在背包还放得下这件物品时，选与不选都试一下，选二者的较大值
情况2：在背包放不下这件物品的时候，直接跳过这件物品
递归出口： 没有物品可选

分析好这些所有的必备条件后，代码就很简单了
普通递归代码

public int rec(int i,int j){
		int res;
		if(i==n){//递归出口
			res = 0;
		}else if(j<w[i]){//背包放不下这个物品
			res = rec(i+1,j);
		}else{//放与不放都试一下，取较大者
			res = Math.max(rec(i+1,j),rec(i+1,j-w[i])+v[i]);
		}
		return res;
	}

记忆搜索式递归

用一个记忆数组dp储存上面递归生成的数据，防止重复递归，避免浪费。

int dp[][] = new int[n+1][W+1];
public int rec1(int i,int j){
		if(dp[i][j]>0)return dp[i][j];
		int res;
		if(i==n){//递归出口
			res = 0;
		}else if(j<w[i]){//背包放不下这个物品
			res = rec1(i+1,j);
		}else{//放与不放都试一下，取较大者
			res = Math.max(rec1(i+1,j),rec1(i+1,j-w[i])+v[i]);
		}
		return dp[i][j]=res;
	}

穷竭搜索式递归

public int rec2(int i,int j,int sum){
		int res;
		if(i==n){//递归出口
			res = sum;
		}else if(j<w[i]){//背包放不下这个物品
			res = rec2(i+1,j,sum);
		}else{//放与不放都试一下，取较大者
			res = Math.max(rec2(i+1,j,sum),rec2(i+1,j-w[i],sum+v[i]));
		}
		return res;
	}

逆向动态规划

从上面的分析很容易得出动态规划方程
没有物品选
dp[n][j]=0
选不了这个物品
dp[i][j]=dp[i+1][j]
选与不选取较大者
dp[i][j]=Math.max(dp[i+1][j],dp[i+1][j-w[i]]+v[i])`
dp[i][j]表示从第i个物品开始选择总重小于等于j的部分

int dp[][] = new int[n+1][W+1];
public int dp(){
		//这样设计动态规划方程这里必须逆向循环，因为只有i=n的时候是出口
		for(int i=n-1;i>=0;i--){
			for(int j=0;j<=W;j++){
				if(j<w[i]){
					dp[i][j] = dp[i+1][j];
				}else{
					dp[i][j] = Math.max(dp[i+1][j], dp[i+1][j-w[i]]+v[i]);
				}
			}
		}
		return dp[0][W];
	}

正向动态规划

上面动态规划是逆向的，要想正向的话，必须重新设计动态规划方程。
dp[i+1][j]表示从前i个物品选择总重小于等于j的物品
dp[0][j]=0
dp[i+1][j]=dp[i][j] (j dp[i+1][j]=Math.max(dp[i][j],dp[i][j-w[i]]+v[i])

int dp[][] = new int[n+1][W+1];
public int dp1(){
		for(int i=0;i<n;i++){
			for(int j=0;j<=W;j++){
				if(j<w[i]){
					dp[i+1][j] = dp[i][j];
				}else{
					dp[i+1][j] = Math.max(dp[i][j], dp[i][j-w[i]]+v[i]);
				}
			}
		}
		return dp[n][W];
	}