最速下降方法与Newton方法

《Convex Optimization》

最速下降方法

$f(x+v)$在$v=0$处的一阶泰勒展开为：
$$f(x+v)\approx \hat{f}(x+v)=f(x)+\nabla f(x{)}^{T}v$$
$\nabla f(x{)}^{T}v$是$f$在$x$处沿$v$的方向导数。它近似给出了$f$沿小的步径$v$会发生的变化。
在$v$的大小固定的前提下，讨论如何选择$v$使得方向导数最小是有意义的，即：
$$\Delta x_{nsd}=argmin\{\nabla f(x{)}^{T}v|\Vert v\Vert =1\}$$
最速下降方向就是一个使$f$的线性近似下降最多的具有单位范数的步径。注意，这里的单位范数，并不局限于Euclid范数。
我们先给出最速下降方法的算法，再介绍几种范数约束。

Euclid范数和二次范数

Euclid范数

显然，这时的方向就是负梯度方向。

二次范数

我们考虑二次范数
$$\Vert z{\Vert }_P=(z^{T}Pz{)}^{1/2}=\Vert P^{1/2}z\Vert$$
其中P为n阶对称正定矩阵。

这时的最优解为：
$$\Delta x_{nsd}=-(\nabla f(x{)}^T{P}^{-1}\nabla f(x){)}^{-1/2}{P}^{-1}\nabla f(x)$$
这个最优解，可以通过引入拉格朗日乘子，求解对偶函数KKT条件获得，并不难，就不写了。

基于坐标变换的解释

二次范数，可以从坐标变换的角度给出一个解释。
我们定义线性变换：
$$\bar{u}=P^{1/2}u$$
那么：
$$g(\bar{u})=f(P^{-1/2}\bar{u})=f(u)$$
$g$在$\bar{x}$出的负梯度方向为：
$$\Delta \bar{x}=-\nabla \bar{f}(\bar{x})=-P^{-1/2}\nabla f(P^{-1/2}\bar{x})=-P^{-1/2}\nabla f(x)$$
注意，并没有归一化。
又，我们已经知道$\Delta x=-P^{-1}\nabla f(x)$(只是方向而已)，所以：
$$\Delta \bar{x}=P^{1/2}\Delta x$$
同样的线性变换。换言之，二次范数$\Vert \cdot {\Vert }_P$下的最速下降方向可以理解为对原问题进行坐标变换$\bar{x}=P^{1/2}x$后的梯度方向。辅以下图便于理解。

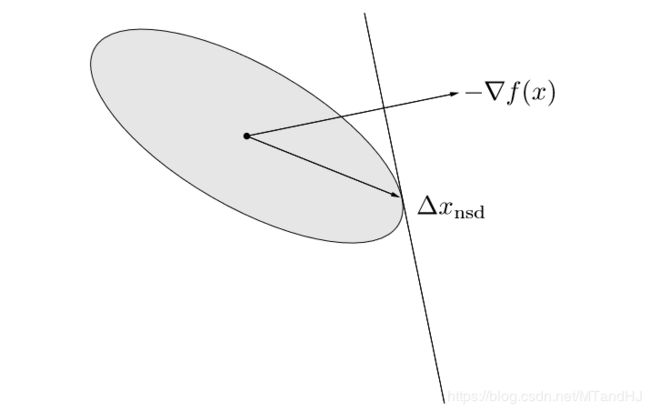
采用${\ell }_1$-范数的最速下降方向

这个问题的刻画如下：
$$\Delta x_{nsd}=argmin\{\nabla f(x{)}^{T}v|\Vert v{\Vert }_1=1\}$$
${\ell }_1$即各分量绝对值之和，所以，只需把$\nabla f(x)$绝对值分量最大的那个部分找出来即可。不妨设，第$i$个分量就是我们要找的，那么：
$$\Delta x_{nsd}=-sign(\frac{\partial f(x)}{\partial x_i})e_i$$
其中，$e_i$表示第$i$个基向量。
所以，在每次下降过程中，都只是改变一个分量，所以${\ell }_1$-范数的下降，也称为坐标下降算法。
辅以下图以便理解：

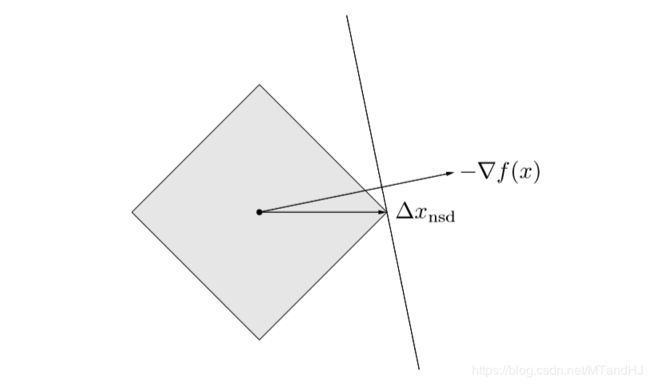
至于收敛性分析，与先前的相反，我们不在这里给出（打起来太麻烦了实际上，有需求直接翻书就好了）。

数值试验

我们依然选择$f(x)=e^{x_1+3x_2-0.1}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}$，$\alpha =0.2,\beta =0.7$，初始点为$(7,3)$，下图为我们展示了一种较为极端的坐标下降的方式。

代码只需要改变gradient2的几行而已。

def gradient2(x):
    x0 = x[0]
    x1 = x[1]
    grad1 = np.exp(x0+3*x1-0.1) \
            + np.exp(x0-3*x1-0.3) \
            - np.exp(-x0-0.1)
    grad2 = 3 * np.exp(x0+3*x1-0.1) \
            -3 * np.exp(x0-3*x1-0.3)
    if abs(grad1) > abs(grad2):
        return np.array([grad1/abs(grad1),0])
    else:
        return np.array([0, grad2/abs(grad2)])

Newton 方法

最开始看的时候，还很疑惑，后来才发现，原来这个方法在很多地方都出现过。除了《凸优化》(《Convex Optimization》)，数学分析（华师大）和托马斯微积分都讲到过。虽然，或者将的一元的特殊情况，而且，后者的问题是寻找函数的零值点。起初，还不知道怎么把俩者联系起来，仔细一想，导函数的零值点不就是我们所要的吗？当然，得要求函数是凸的。

实际上，Newton方法是一种特殊的二次范数方法。特殊在，$P$的选取为Hessian矩阵${\nabla }^{2}f(x)。$我们还没有分析，二次范数的$P$应该如何选择。在下降方法的收敛性分析中，我们强调了条件数的重要性。加上刚刚分析过的坐标变换，坐标变换后，新的Hessian矩阵变为：
$$P^{-1/2}{\nabla }^{2}f(x)P^{-1/2}$$
所以，如果我们取$P={\nabla }^{2}f(x^{\ast })$，那么新的Hessian矩阵在最有点附近就近似为$I$，这样就能保证快速收敛。如果，每次都能选择$P={\nabla }^{2}f(x)$，这就是Newton方法了。下图反映了为什么这么选择会加速收敛：

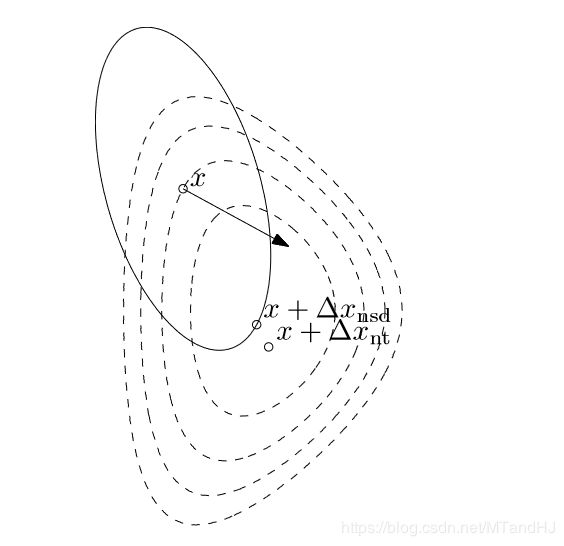
Newton 步径

Newton步径：
$$\Delta x_{nt}=-{\nabla }^{2}f(x{)}^{-1}\nabla f(x)$$
则：
$$\nabla f(x{)}^T\Delta x_{nt}=-\nabla f(x{)}^T{\nabla }^{2}f(x{)}^{-1}\nabla f(x)<0$$
因为我们假设Hessian矩阵正定，所以上述不等式在$\nabla f(x)̸=0$时都成立。

二阶近似的最优解

$f(x+v)$在$v=0$处的二阶近似为：
$$\hat{f}(x+v)=f(x)+\nabla f(x{)}^{T}v+\frac{1}{2}{v}^T{\nabla }^{2}f(x)v$$
这是$v$的二次凸函数，在$v=\Delta x_{nt}$处到达最小值。下图即是该性质的一种形象地刻画：

线性化最优性条件的解

如果我们在$x$附近对最优性条件$\nabla f(x^{\ast })=0$处进行线性化，可以得到：
$$\nabla f(x+v)\approx \nabla f(x)+{\nabla }^{2}f(x)v=0$$
这个实际上就是我在最开始对Newton方法的一个解释。不多赘述。

Newton 步径的仿射不变性

这个在代数里面是不是叫做同构？

Newton 减量

我们将
$$\lambda (x)=(\nabla f(x{)}^T{\nabla }^{2}f(x{)}^{-1}\nabla f(x){)}^{1/2}$$
称为Newton减量。
有如下的性质：
$$f(x)=\underset{y}{\inf }\hat{f}(y)=f(x)-\hat{f}(x+\Delta x_{nt})=\frac{1}{2}\lambda (x{)}^2$$
$$\lambda (x)=(\Delta x_{nt}^T{\nabla }^{2}f(x)\Delta x_{nt}{)}^{1/2}$$
$$\nabla f(x{)}^T\Delta x_{nt}=-\lambda (x{)}^2$$
Newton步径同样是仿射不变的。
Newton步径常常用作停止准则的设计。

Newton 方法

算法如下：

收敛性分析

收敛性分为俩个阶段，证明比较多，这里只给出结果。

第一阶段为阻尼Newton阶段，第二阶段为二次收敛阶段。

数值实验

我们依然选择$f(x)=e^{x_1+3x_2-0.1}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}$，$\alpha =0.2,\beta =0.7$，初始点为$(7,3)$，下图采用牛顿方法的图（代码应该没写错吧）。

下图初始点为$(-5,3)$

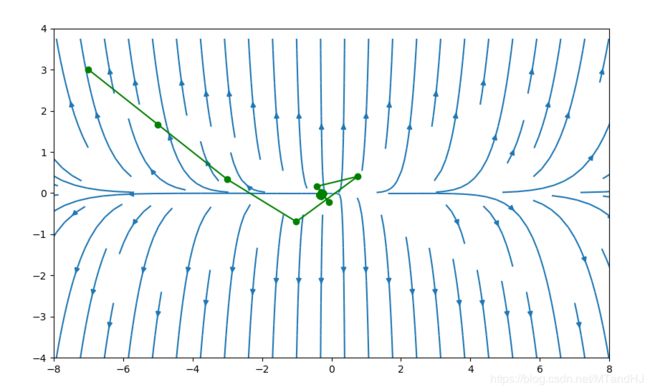
代码

def hessian(x):
    x0 = x[0]
    x1 = x[1]
    hessian = np.zeros((2, 2), dtype=float)
    element1 = np.exp(x0 + 3 * x1 - 0.1)
    element2 = np.exp(x0 - 3 * x1 - 0.1)
    element3 = np.exp(-x0 - 0.1)
    hessian[0, 0] = element1 + element2 + element3
    hessian[0, 1] = 3 * element1 - 3 * element2
    hessian[1, 0] = 3 * element1 - 3 * element2
    hessian[1, 1] = 9 * element1 + 9 * element2

    return np.linalg.inv(hessian)

下降方法也修改了一下：

    def grad3(self, gradient, alpha, beta, error=1e-5):
        """回溯直线收缩算法 Newton步径
        gradient: 梯度需要给出
        alpha: 下降的期望值 (0, 0.5)
        beta:每次更新的倍率 (0, 1)
        error: 梯度的误差限，默认为1e-5
        """
        assert hasattr(gradient, "__call__"), \
            "Invalid gradient"
        assert 0 < alpha < 0.5, \
            "alpha should between (0, 0.5), but receive {0}".format(alpha)
        assert 0 < beta < 1, \
            "beta should between (0, 1), but receive {0}".format(beta)
        error = error if error > 0 else 1e-5

        def search_t(alpha, beta, grad, hessian_inv):
        	"""回溯"""
            t = 2
            t_old = 2
            step = grad @ hessian_inv
            grad_module = grad @ step
            assert grad_module >= 0, "wrong in grad_module"
            while True:
                newx = self.x + t * step
                newy = self.__f(newx)
                if newy < self.y - alpha * t * grad_module: 
                    return t_old
                else:
                    t_old = t
                    t = t_old * beta
        while True:
            grad = -gradient(self.x)
            hessian_inv = hessian(self.x)
            t = search_t(alpha, beta, grad, hessian_inv)
            x = self.x + t * grad @ hessian_inv
            lam = grad @ hessian_inv @ grad
            if lam / 2 < error: #判别准则变了
                break
            else:
                self.x = x
                self.y = self.__f(self.x)
                self.__process.append((self.x, self.y))