【课程设计】 哈夫曼树的应用:字符串的加密与解密
一.实验任务
在一个加密应用中,要处理的信息来自下面的字符集,各个字符的相关使用频度如下:
字符空格 A B C D E F G H I J K L M
频度 180 64 13 23 32103 2215 47 57 1 5 31 20
字符 N O P Q R S T U V W X Y Z
频度 55 63 15 1 48 56 8025 7 18 2 16 1
现请编写程序你实现如下功能:
(1)运行时,由用户输入来初始化字符集大小和相应用字符。
(2)输入一个要加密的字符串,将其加密。
(3)输出解密字符串。
二.功能
(1)输入一串字符,建立哈夫曼树
(2)得到哈夫曼编码
(3)实现哈夫曼译码
三.基本思想
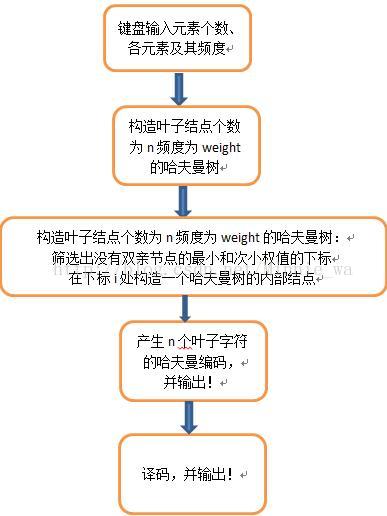
(1)初始化:输入字符以及其频度
构造哈夫曼树
构造哈夫曼树基本思想:
(2)加密:输入字符,输出哈夫曼编码
(3)解密::输入哈夫曼编码,输出字符代码
(4)退出
四.数据结构与算法分析
应用哈夫曼树
该哈夫曼树采用双亲孩子表示法存储,构造哈夫曼树的叶子结点有n个,合并次数n-1,则森林中公有2n-1棵树
1.哈夫曼树结点构造
定义节点结构体,结构体类型名为huffnode
typedef struct {
char data; //节点值
int weight; //结点的权重
int parent; //双亲结点
int lchild; /保存该结点的左孩子结点右孩子结点在数组中的位置
int rchild; //保存该结点的右孩子结点右孩子结点在数组中的位置
} huffnode;
2.哈夫曼编码结构,结构体类型名为huffcode
typedef struct {
charcd[MAX]; //存放哈夫曼编码
intstart; //编码的起始下标
}huffcode;
3.主函数五.完整程序代码
#include
#include
#include
#define MAX 26 //节点允许的最大数量26
/*哈夫曼树结点结构*/
typedef struct { //定义一个新数据类型即结点结构
char data; //节点值
int weight; //结点的权重
int parent; //保存该结点的双亲结点在数组中的下标
int lchild; //保存该结点的左孩子结点在数组中的位置
int rchild; //保存该结点的右孩子结点右孩子结点在数组中的位置
} huffnode; //定义结构体类型名为huffnode
/*哈夫曼编码结构*/
typedef struct { //定义保存一个叶子结点的哈夫曼树编码的结构
char cd[MAX]; //存放哈夫曼编码
int start; //编码的起始下标
} huffcode; //编码结构体类型名为huffcode
/*主函数*/
int main() {
huffnode ht[2*MAX]; //定义一个数组,用于存放哈夫曼树的各个节点信息
huffcode hcd[MAX], d; //定义huffmancode类型的hcd【】数组和huffmancode类型的变量d,用于保存每个结点到根节点路径所对应的编码
int i, j, f, l, r, n, c, s1, s2;
cout<<"* * * * * * * * * * * * * * * * * * * * * ** * * * * * \n" <<"\n加密应用:对字符串进行加密与解密\n" <<"* * * * * * * * * * * * * * ** * * * * * * * * * * * * \n";
/*用户输入来初始化字符集大小和相应用字符及其频度*/
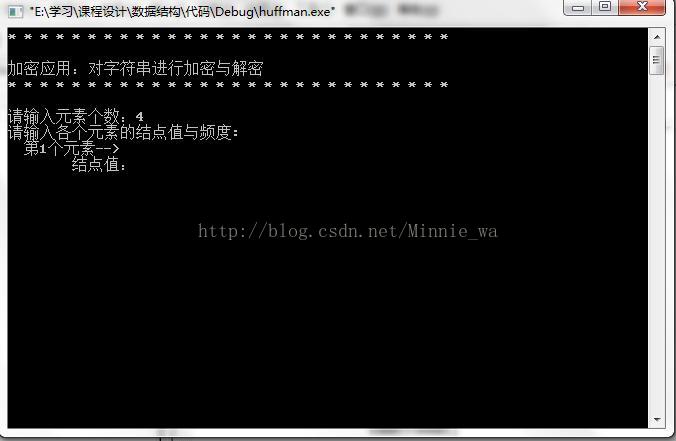
cout<<"\n请输入元素个数:";
cin>>n;
cout<<"请输入各个元素的结点值与频度:\n";
for(i=1;i<=n;i++) {
cout<<" 第"<
cin>>&ht[i].data;
cout<<"\t频 度:";
cin>>ht[i].weight;
}
/*构造叶子节点个数为n权值为weight的哈夫曼树*/
for(i=1;i<=2*n-1;i++) /*初始化,所有结点均没有双亲和孩子*/
ht[i].parent=ht[i].lchild=ht[i].rchild=0;
for(i=n+1;i<=2*n-1;i++) /*构造哈夫曼树n-1个非叶节点*/
{
s1=s2=32767; //用来保存权重最小和次小的两个值(即找出权重最小的,分别用s1,s2保存)
l=r=0; //lr是用来保存最小和次小的两个结点
for(j=1;j<=i-1;j++) /*循环找出所有权重中最小的两个值(即筛选出没有双亲节点的最小和次小权值的下标)*/
if(ht[j].parent==0) //如果是某棵子树的根节点j
if(ht[j].weight
{
s2=s1; //次小权重为s1的权重
r=l; // 次小值为l
s1=ht[j].weight; //最小权重为k的权重
l=j; //最小值为j
}
else if(ht[j].weight
{
s2=ht[j].weight; //次小权重S2的值为j的权重
r=j; //次小值为j(最小值为l)
}
/*在下标i处构造一个哈夫曼树的内部结点*/
ht[l].parent=i;
ht[r].parent=i; //最小结点和次小结点的双亲结点在数组中的下标为i
ht[i].weight=ht[l].weight+ht[r].weight; //双亲结点的权重
ht[i].lchild=l;
ht[i].rchild=r; //双亲结点的左、右孩子分别为l和r
}
/*产生n个叶子字符的哈夫曼编码*/
for(i=1;i<=n;i++)
{
d.start=n+1; //不等长编码的起始位n+1
c=i; //c为结点在数组中的下标
f=ht[i].parent; //f为结点的双亲结点在数组中的下标
while(f!=0) { //从叶节点开始往根节点走,每往上走一层(即从叶子扫描至根),就产生一位编码存入hcd[]中
if(ht[f].lchild==c)
d.cd[--d.start]='0'; //左孩子编码为0
else
d.cd[--d.start]='1'; //右孩子编码为1
c=f;
f=ht[f].parent;
}
hcd[i]=d; //保存每个叶节点的编码
} /*以上哈夫曼树构造完毕*/
cout<<"输出哈夫曼编码:\n";
for(i=1;i<=n;i++) {
cout<
for(j=hcd[i].start;j<=n;j++)
cout<
cout<<"\n";
}
l: cout<<"\n请选择加密/解密/退出: (B/Y/E): ";
char hfm;
cin>>hfm;
if(hfm=='e')
return 0;
else {
switch(hfm)
{
case'b':
{
int q ;
char bs;
cout<<"\n* * * 哈夫曼字符串加密 * * *\n";
cout<<"请输入要加密的字符串: "<
for(q=0;bs!=10;q++)
{
bs=getchar();
for(i=1;i<=n;i++)
{
if (bs==ht[i].data)
for(j=hcd[i].start;j<=n;j++)
cout<
}
}
cout<
}break;
case'y':
{
char e;
int t,u;
t=2*n-1;
cout<<"\n* * * 哈夫曼解密 * * *\n";
cout<<"\n请输入哈夫曼编码: "<
for(u=0;e!=10;u++)
{
if(ht[t].lchild!=0)
{
e=getchar();
if(e=='0')
t=ht[t].lchild;
else
t=ht[t].rchild;
}
else
{
cout<
t=2*n-1;
}
}
cout<
}
break;
}
goto l;
}
return 0;
} //Huffman
六.运行结果
进入界面

输入元素个数,元素及其频度
得到每个字符的 哈夫曼编码

编辑:b————进行编码
编辑y——-进行译码