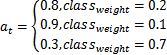Focal loss 原理及keras实现

一、keras原理

focal loss就是在cross_entropy_loss前加了权重，让模型注重于去学习更难以学习的样本，并在一定程度上解决类别不均衡问题。在理解focal loss前，一定要先透彻了解交叉熵cross entropy。

1、Cross entropy

交叉熵部分的内容来自博客，对交叉熵写的很详细，深入浅出。感谢该博主

1）信息熵H（x）

一个随机变量的信息量，直观上去感受就是发生概率下的时间带来的信息量更大，发生概率更大的事件信息量小。也就是一个成反比的函数。在信息论中，被定义为：

 

假设一个随机事件有n种可能性，那么该随机时间信息量的期望就是熵。 

   

2）相对熵

相对熵也叫KL散度，用来衡量两个随机分布的差异，定义为：

由于，-H（p）为负的P的信息熵，是个固定值。因此只需要计算后半部分来衡量两个概率分布的差异即可，后半部分就是我们经常提及的交叉熵。

3）交叉熵

衡量两个分布的差异，经常作为多分类模型的损失函数。

4）交叉熵在keras中的使用方法。

keras中交叉熵损失函数定义如下：

def Cross_entropy_loss(y_true,y_pred):
    '''

    :param y_true: ont-hot encoding ,shape is [batch_size,nums_classes]
    :param y_pred: shape is [batch_size,nums_classes],each example defined as probability for per class
    :return:shape is [batch_size,], a list include cross_entropy for per example
    '''
    y_pred = K.clip(y_pred, K.epsilon(),1.0 - K.epsilon())
    crossEntropyLoss = -y_true * tf.log(y_pred)
 
    return tf.reduce_sum(crossEntropyLoss,-1)

需注意以下几点：

a)y_true:shape为[batch_size,num_classes]，batch数据标签签one-hot编码，y_pred：shape同样为[batch_size,num_classes]，batch数据模型预测的每一类的概率。数据样例如下：

y_true = np.array([[0,0,1],
                  [1,0,0],
                  [0,1,0]])
y_pred = np.array([[0.1,0.1,0.8],
                   [0.5,0.4,0.1],
                   [0.2,0.6,0.2]])

b)要避免y_pred某一类的预测概率为0，因为-log 0 的值为无穷大inf，会导致loss出现nan。用K.epslion() 一个极小值替换0。

c)注意返回值是一个list，长度为batch_size。由每个样本的交叉熵组成的list。 

比较我们按以上理解实现的cross entropy与keras定义的函数是否一样，代码如下：

import tensorflow as tf
import numpy as np
import tensorflow.keras.backend as K

from tensorflow.keras.losses import categorical_crossentropy,binary_crossentropy


def Cross_entropy_loss(y_true,y_pred):
    '''
    :param y_true:
    :param y_pred:
    :return:
    '''
    y_pred = K.clip(y_pred, K.epsilon(),1.0 - K.epsilon())
    crossEntropyLoss = -y_true * tf.log(y_pred)
    crossEntropyLoss1 = categorical_crossentropy(y_true,y_pred)
    return crossEntropyLoss,crossEntropyLoss1,tf.reduce_sum(crossEntropyLoss,-1)

y_true = tf.placeholder(shape=(None,None),dtype=tf.float32,name='y')
y_pred = tf.placeholder(shape=(None,None),dtype=tf.float32,name='p')
CEloss,CEloss1,CEloss_sum = Cross_entropy_loss(y_true,y_pred)

y1 = np.array([[0,0,1],[1,0,0],[0,1,0]])
y_p = np.array([[0.1,0.1,0.8],[0.5,0.4,0.1],[0.2,0.6,0.2]])
#如果预测值为0 log(0)是inf 导致loss为nan 所以要避免出现0 用epsilon代替0

with tf.Session() as sess:
    t,t1,cl = sess.run([CEloss,CEloss1,CEloss_sum],feed_dict={y_true:y1,y_pred:y_p})
    print(t)
    print(t1)
    print(cl)

运行结果如下： 

[[0.         0.         0.22314353]
 [0.6931472  0.         0.        ]
 [0.         0.5108256  0.        ]]
[0.22314353 0.6931472  0.5108256 ]
[0.22314353 0.6931472  0.5108256 ]

2、focal loss

focal loss就是在cross entropy的基础上加上权重。让模型注重学习难以学习的样本，训练数据不均衡中占比较少的样本，如果将cross loss定义为：

那focal loss加权后的定义是

相信很多人都迷惑，pt是什么。对一个样本来说，pt就是该样本真实的类别，模型预测样本属于该类别的概率。例如某样本的label是[0,1,0]，模型预测softmax输出的各类别概率值为[0.1,0.6,0.3]。该样本属于第二类别，模型预测该样本属于第二类别的概率是0.6。这就是pt。pt实际上就是个阶段函数。

为什么pt这么定义，我们先来求下上例的cross entropy是多少，

          

由上面求解过程可知，cross entropy的累加项中只有一个不为0，就是该样本真实类别的这项， loss为-log(pt)，pt可理解为指示函数，指示对于某样例，模型预测该样例属于真实类别的概率值。

如果是二分类的话，是个特例。由于这两个的概率值互斥（总和为1），pt定义如下，也就是论文中的公式。其实和多分类一样，只是知道其中一类的概率p(x)，另一类的概率用1-p(x)表示而已。

理解为pt后，整个公式就很好理解了。就是在cross loss前加上了两个权重像at和（1-pt）**gamma，分别来解释这两个权重项是怎么定义的，有什么作用。

1）at项

at项用来处理类别不均衡问题，类似于机器学习中训练样本的class_weight。也是个指示函数。例如训练样本中个类别占比为20%，10%，70%。那么at可以定义如下。其实就是某类别占比较高，就将该类别设置一个较小的权重a，占比较低就将其设置一个将大的权重a。降低占比高的loss。提高占比低的loss

2)(1-pt)**gamma项

个人认为该项有两个作用：

a)让模型专注于训练难训练的样本，对于模型所属的真实类别，模型的预测值pt的值接近1，说明该样本容易训练，pt值接近0（模型预测该样本属于真实类别的概率是0就说明错的很离谱），样本难以训练。提高难以训练样本的loss。降低好训练样本的loss。pt∈[0,1]。同样(1-pt)∈[0,1]。(1-pt)**gamma符合我们的要求。(满足我们需求的函数很多，并不强制要求为此函数）

 b)一定程度上也能解决类别不均衡问题。我们经常会遇到一个问题，如果在二分类中，负样本占比0.9。此时模型倾向于将样本全部判负。考虑正常CE loss中，由于正负样本的权重一样。CE LOSS包含两部分（90%的负样本（模型判别正确），10%的正样本模型判别错误）。也就是错误样本带来的loss在CE LOSS中只占10%。加上(1-pt)**gamma项后，会提高正样本判负的loss在总loss中的比重。