KMP模式匹配算法

KMP模式匹配算法

KMP算法可以说是一个很经典的模式匹配算法了，刚开始并没有看懂，多看几遍就好了。

朴素模式匹配算法（KMP算法没提出来之前的常用的匹配算法）

当我们在一篇文章中去搜索一个单词的时候，就是在文章中对这个单词进行定位操作。这种子串的定位操作通常称为串的模式匹配。是字符串中最重要的操作之一。模式匹配就是给定两个字符串O和F，长度分别为n和m，判断F是否在O中，如果出现则返回出现的位置。

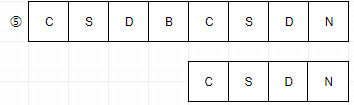
例如我们要从主串S="csdbcsdn"中，找到T="csdn"这个子串的位置，我们通常需要以下的步骤：

1：主串S第一位开始，S与T的前三个字母都匹配成功，但是S的第四个位置跟T的第四个位置不同，所以第一位匹配失败。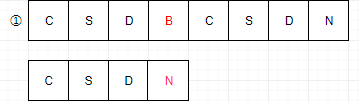

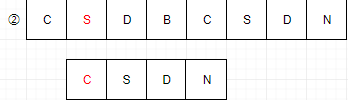
2：主串S第二位开始，S的首字母是s，子串T的首字母是c，匹配失败

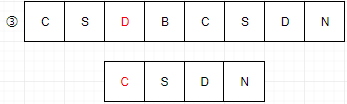
3：主串S第三位开始，S的首字母是d，子串T的首字母是c，匹配失败

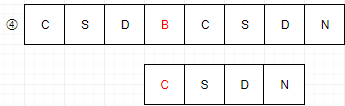
4：主串S第四位开始，S的首字母是b，子串的首字母是c，匹配失败

5：主串S第五位开始，S与T，4个字母全匹配，匹配成功。

简单的说，就是对主串的每一个字符作为子串的开头，与要匹配的字符串进行匹配。对主串做最大循环，每个字符开头做T的长度的小循环，直到匹配成功或全部遍历完为止。

#朴素模式匹配
#include
#include
int IndexString (char S[10],char T[10],int pos)
{
	int i=pos; /*use to index the location of S */
	int j=0; /*use to index the location of T*/
	int slen; /*the length of String S*/
	int tlen; /* the length of String T*/
	slen=strlen(S);
	tlen=strlen(T);
	while(i=tlen)
	{
		return (i-tlen);
	}else
		return 0;
}
int main()
{
	char S[10];
	char T[10];
	int a;
	scanf("%s",&S);
	scanf("%s",&T);
	a=IndexString(S,T,0);
	printf("%d\n",a);
}

因为在实际应用中，对于计算机来说，处理的都是二进位的0和1的串，例如出现0000000000000000001110000的主串，然后匹配11100子串，这样的话，效率是很低下的。

为了解决朴素模式匹配算法的低效，三位前辈D.E.Knuth,J.H.Morris和V.R.Pratt发表了一个模式匹配算法，可以大大避免重复遍历的情况，这个算法就是KMP。

KMP模式匹配算法原理

在介绍kmp之前我们需要先了解一下前缀和后缀是什么。

  前缀：指的是字符串的子串中从原串最前面开始的子串，如abcdef的前缀有：a,ab,abc,abcd,abcd。

  后缀：指的是字符串的子串中在原串结尾处结尾的子串，如abcdef的后缀有：f,ef,def,cdef,bcdef。

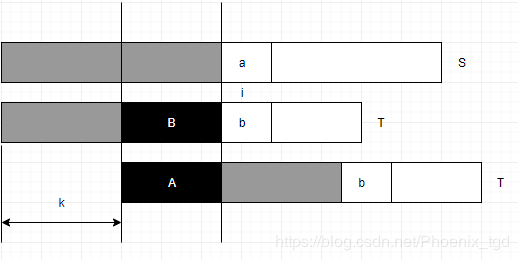
kmp算法的思想：在字符串S中寻找T，当匹配到位置 i 时两个字符串不相等，，此时我们需要将字符串T向前移动。在这里我们可以提前计算某些信息，就有可能一次前移多位。假设，我们根据分析两个字符串可以得知可以向前移动k位，分析T字符串有以下特征：

1：A段字符串是T的一个前缀

2：B段字符串是T的一个后缀

3：A段字符串和B段字符串相等

所以前移k位之后，我么继续比较位置 i 的前提是T的前i-1个位置满足：长度为i-k-1的前缀A和后缀B相同，只有这样我们才可以前移k位后从新的位置继续比较。

    所以kmp算法的核心即是计算字符串T每一个位置之前的字符串的前缀和后缀公共部分的最大长度（不包括字符串本身，否则最大长度始终是字符串本身）。获得T每一个位置的最大公共长度之后，就可以利用该最大公共长度快速和字符串S比较。当每次比较到两个字符串的字符不同时，我们就可以根据最大公共长度将字符串T向前移动(已匹配长度-最大公共长度)位，接着继续比较下一个位置。事实上，字符串f的前移只是概念上的前移，只要我们在比较的时候从最大公共长度之后比较f和O即可达到字符串T前移的目的。

 next数组值推导 

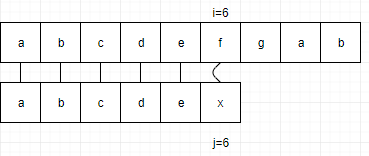
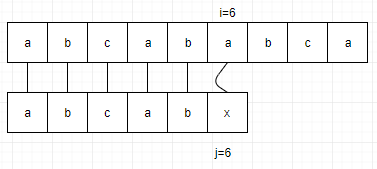
例如，当S="abcdefgab",由于T="abcdex"，当中没有任何重复的字符，所以T的位置 j 就由6变到1。

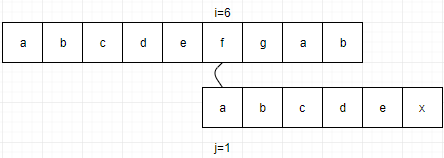
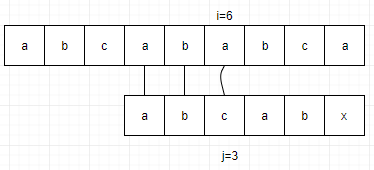
当S="abcababca"，T="abcabx"，前缀的"ab"与最后的"x"之前的串"ab"是相等的，所以 j 就由6变为了3。

 

因此，我们就可以得出规律，j 值的多少取决于当前字符串之前的串的前后缀的相似度。我们把T串各个位置的 j 值变化定义为一个数组next，那么next的长度就是T串的长度。

例如：

1：T="abcdex"

j	123456
模式串T	abcdex
next[j]	011111

1)：当j=1时，next[1]=0

2)：当j=2时，j由1到j-1只有字符"a"，属于其他情况，next[2]=1

3)：当j=3时，j由1到j-1有字符"ab"，字符"ab"的前缀为"a"，后缀为"b"，不相等，属于其他情况，next[3]=1

4)：后面同理，所以最终T串的next[j]为011111

2：T="abcabx"

j	123456
模式串T	abcabx
next[j]	011123

1)：当j=1时，next[1]=0

2)：当j=2时，j由1到j-1只有字符"a"，所以next[2]=1

3)：当j=3时，j由1到j-1的字符为"ab"，前缀为"a"，后缀为"b"，不相等，所以next[3]=1

4)：当j=4时，同上，next[4]=1

5)：当j=5时，1到j-1 的字符串为"abca",前缀字符"a"与后缀字符"a"相等，所以可以算出k=2，所以next[5]=2

6)：当j=6时，1到j-1 的字符串为"abcab"，前缀字符"ab"与后缀字符"ab"相等，所以可以推算出k=3,所以next[6]=3

#include
#include
void get_next(char t[],int next[])
{
	int i,j;
	int tlen=strlen(t);
	i=1;
	j=0;
	next[1]=0;
	while(i=tlen)
		return (i-tlen);
	else
		return 0;
}
int main(){
	int i;
	int next[20]={0};
	char s[10];
	char t[10];
	int a,tlen;
	scanf("%s",&s);
	scanf("%s",&t);
	tlen=strlen(t);
	a=Index_KMP(s,t,next);
	for(i=1;i<=tlen;i++)
	{
		printf("%d ",next[i]);		
	}
	printf("\n");
	printf("%d\n",a);
}

KMP模式匹配算法改进

后来有人发现，KMP还是有缺陷的。我们对next函数进行了改良。取代next的数组为nextval数组。

nextval数组的推导

1：T="ababaaaba"

j	123456789
模式串T	ababaaaba
next[j]	011234223
nextval[j]	010104210

先算出next数组的值分别为011234223，然后再做判断

1)：当j=1时，nextval[1]=0

2)：当j=2时，因为第二位字符"b"的next值是1，而第一位就是"a"，他们不相等，所以nextval[2]=next[2]=1

3)：当j=3时，第三位字符"a"的next值为1，而第一位是"a"，他们相等，所以nextval[3]=nextval[1]=0

4)：当j=4时，第四位字符"b"的next值为2，而第二位为"b"，他们相等，所以nextval[4]=nextval[2]=1

依次按照这个来判断，所得到的nextval为010104210.

void get_nextval(char t[],int nextval[])
{
	int i,j;
	int tlen=strlen(t);
	i=1;
	j=0;
	nextval[1]=0;
	while(i