SIFT算法系列之尺度空间

尺度空间定义

　　说到尺度空间理论最早可以追溯到1962年的T.Iijima最先提出，学术界开始关注尺度空间技术主要在1986年IEEE PAMI上同时刊出的4篇关于尺度空间理论的文章奠定了发展基础。现实世界中物体只有具备一定的尺度才能够倍人眼所察觉，计算机视觉学术研究就是在不断的尝试与突破来模拟人眼的观察方法。因此，尺度空间就是试图在图像领域中模拟人眼观察物体的概念与方法。例如：观察一颗树，关键在于我们想要观察是树叶子还是整棵树：如果是一整棵树(相当于大尺度情况下观察)，那么就应该去除图像的细节部分。如果是树叶(小尺度情况下观察)，那么就该观察局部细节特征。

　　构建尺度空间的过程中，其实是在不断的去除细节过程同时不能够引进新的错误细节特征。想想尺度空间金字塔进行高斯滤波时候，原始图像保存最多的细节特征，经过高斯滤波后细节特征逐渐减少来模拟大尺度情况下的特征表示。那么，什么是尺度空间？能否给尺度空间技术有个数学上定义或者判断准则呢？示例参考于:

图1 第一组角 图2 第二组角 图3 第三组角 图4 第四组角 图5 第五组角
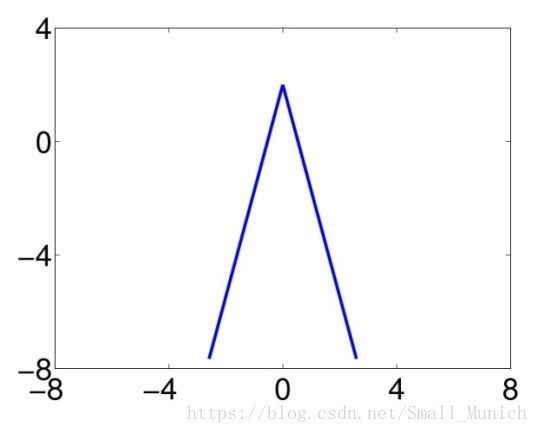
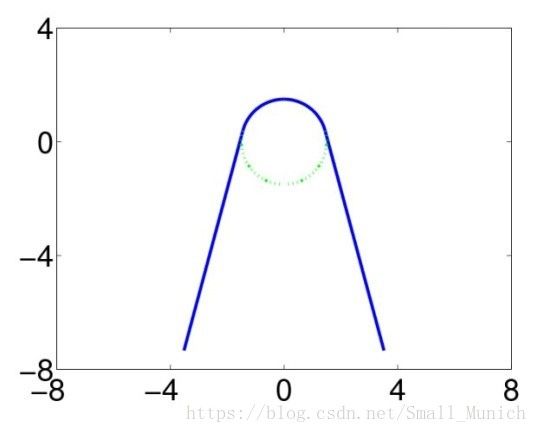
　　从图1-5中示例来观察判断左右哪个角度更为尖锐问题。图1中可以清楚的判断出右边更为尖锐(左边圆钝)，因为从数学概念上其角度值小。图2中可以判断右边的尖锐，因为从数学上其曲率值小。图3中判断哪个更为尖锐相对困难一些。右边的具有大的角度值（圆钝）又有较大的曲率值（尖锐），左边刚好相反。所以在图3中判断哪个角更为尖锐已经不在是纯粹的数学概念可以获取明确答案。准确的说，这是计算机视觉中的尺度空间理论的视觉问题，答案取决于观察物体所在的尺度而不是数学上的指标。图4表示在大尺度下观察（远距离），答案是左边的角尖锐。图5表示在小尺度下观察（近距离），答案结果是右边的角度比较尖锐。在这里：尺度空间可以被理解成为观察物体窗口的大小。

　　尺度空间多为多尺度技术的分支和作为金字塔概念的延伸与发展，一般尺度的概念可以有以下几种表示：

　　1 以图像分辨率作为评判准则(图像在多分辨率情况下展示的物体)。

　　2 人眼观察图像轮廓大小的标准。

　　3 观察物体距离的远近作为判断标准。

　　4 滤波卷积核参数作为判断标准。

　　现实情况下物体距离观察者所处位置的远近而呈现出不同的表达，如人眼观察物体在不同的尺度下感受不同，距离较远时观察到的是主要轮廓区域，近距离下观察到更多的细节信息。大尺度参数情况下，高频信息丢失严重，主要显示大致轮廓信息，高频段细节被称作图像中显著的特征。高频信息在视觉领域易于发现与辨识，能够运用于进行特征提取、目标识别等任务。这就是不同尺度下所带来的效应。计算机视觉中的多尺度技术想要表达的基本思想是大尺度情况下图像模糊轮廓形状是小尺度情况下图像轮廓形状的采样。

尺度空间发展及其分类

　　尺度空间能够很好的模拟人眼观察事物的情况，因此在计算机视觉领域中得到很好的应用。构建尺度空间方法主要分为两类：线性尺度空间与非线性尺度空间。其实线性与非线性尺度空间的主要区别在于滤波核函数的不同。线性尺度空间主要核函数是高斯核函数：其计算简单，高效。同时高斯核函数是唯一的尺度不变核函数尺度不变性论文。但是，高斯函数主要的缺点在于无法有效的分辩均匀区域与边缘区域，都是相同的滤波尺度，导致丢失大量局部细节。所以，针对高斯滤波的缺陷，非线性尺度空间理论被提出与应用。非线性滤波核函数当下主要有：双边滤波、非线性扩散滤波等。非线性滤波函数主要解决高斯滤波无法有效分辨均匀与边缘的判决，因此非线性滤波核函数能够保留更多的(高频)边缘信息同时滤波均匀区域。当然，非线性滤波核函数计算复杂度也随之提升。

SIFT尺度空间生成过程

　　说到SIFT算法在构建尺度空间过程可以归纳为：不同大小的高斯核函数对图像进行卷积滤波同时在层级变换之间进行下采样来构建金字塔模式下的尺度空间。SIFT算法在构建尺度空间时候采取高斯核函数进行滤波，主要原因有两个：1 高斯核函数是唯一的尺度不变核函数。2 DoG核函数可以近似为LoG函数，这样可以使特征提取更加简单。同时，David. Lowe作者在论文中提出将原始图像进行2倍上采样后滤波能够保留更多的信息便于后续特征提取与匹配。其实尺度空间图像生成就是当前图像与不同尺度核参数 σ σ 进行卷积运算后产生的图像。

那么下面就以图像方式表述一下尺度空间构建过程：

图6 尺度空间示意图
　　如上图6尺度空间金字塔构建过程示意图，分别为不同尺度下的卷积滤波后的图像迭代演化。其中 S S 代表每组中层数(即X方向产生卷积图像个数)， O O 为金字塔的塔数(即Y方向图像的列数)。SIFT算法中构建高斯金字塔组数一般计算默认如下：

O=[log2(min(w,h))]−3 O = [ l o g 2 ( m i n ( w , h ) ) ] − 3

　　其中 (w,h) ( w , h ) 分别表示图像的宽高。其中每组中的层数 S S 一般设置为3~5。二维高斯空间函数：

G(xi,yi,σx,σy)=12πσxσyexp(−(x−xi)2+(y−yi)22σxσy) G ( x i , y i , σ x , σ y ) = 1 2 π σ x σ y e x p ( − ( x − x i ) 2 + ( y − y i ) 2 2 σ x σ y )

之所以这么拆开二维高斯函数表述公式，而不是写成下面合并方式：

G(xi,yi,σ)=12πσ2exp(−(x−xi)2+(y−yi)22σ2) G ( x i , y i , σ ) = 1 2 π σ 2 e x p ( − ( x − x i ) 2 + ( y − y i ) 2 2 σ 2 )

目的在于下面解释尺度空间构建过程中如何保持连续性问题。

每组内(单纯X方向)相邻尺度关系为：

σ(S+1)=σS2(1S) σ ( S + 1 ) = σ S 2 ( 1 S )

相邻塔之间(Y方向)尺度关系：

σ(o+1)2(s+sS)=2σo∙2(sS) σ ( o + 1 ) 2 ( s + s S ) = 2 σ o ∙ 2 ( s S )

　　所以无论相邻组内或者组间都是尺度2倍差异关系，二维高斯函数在x与y方向尺度差分别为 2–√ 2 关系，所以图像卷积尺度差为2倍。最终的尺度序列总结公式为：

2(o−1)(σ,kσ,…,k(n−1)σ),k=2(1S) 2 ( o − 1 ) ( σ , k σ , … , k ( n − 1 ) σ ) , k = 2 ( 1 S )

其中 o o 为金字塔组数， n n 为每组金字塔层数。

图7 组间尺度连续性说明图例
　　组件下采样长宽各2倍关系，不是应该尺度差异为4倍关系吗？这里SIFT算法进行下采样时候，是当前尺度的上一层尺度图像进行下采样，这样当前尺度与下采样后的图像尺度差就为2倍关系，这样就能够保持金字塔模式下尺度空间的连续性。

评估尺度空间方法

　　不同滤波核函数构建尺度空间图像后如何进行尺度空间评价？虽然高斯核是唯一的线性尺度不变核函数。但是，采取其它滤波核函数构建后的尺度空间(例如：Box Filter、双边滤波、非线性扩散滤波等等)图像如何进行评价，哪种滤波核函数更好滤除噪声，哪种更能够保持尺度最大程度的不变性等等。文章Is SIFT Scale Invariant？通过数学推导和实验来论证SIFT算法的尺度不变性：主要从1 图像初始尺度已知情况下表明其完全尺度不变性，即使图像初始尺度估计偏差较大也可以通过多尺度方式来减少误差； 2 高斯模糊下对比香农抽样和DFT抽样方法实际有效性。具体推导公式参见论文。其实个人见解评价尺度空间的好坏主要可从以下几个方面：均匀区域变化越大越好，边缘区域变化越小越好。大尺度情况下插值后图像信息损失量越小越好。不要破坏局部区域的像素间关系，期待构建过程中按照等比例过程中进行变化。个人见解，如有错误还请批评指正！

代码下载

Github: https://github.com/SmallMunich/sift_scale_visualstudio2015/tree/master

参考

http://www.cs.ubc.ca/~lowe/pubs.html
http://www.diva-portal.org/smash/get/diva2:457189/FULLTEXT01
http://www.cmap.polytechnique.fr/~yu/publications/IPI_SIFT_scale_invariance.pdf
https://wenku.baidu.com/view/ef3de2f07c1cfad6195fa7d9.html