【数据结构】初入数据结构的堆(Heap)以及Java实现
初入数据结构的堆(Heap)以及Java实现
如果觉得对你有帮助,能否点个赞或关个注,以示鼓励笔者呢?!博客目录 | 先点这里
-
堆的基本概念
- 什么是二叉堆
- 最大堆和最小堆
- 注意点
-
二叉堆
- 实现基础
- 动态数组
- 上浮
- 下沉
- 添加元素
- 取最大值
- 取最大值,同时插入新元素
- 将任意数组堆化
-
二叉堆Java代码实现
- 描述
- 实现功能
- 完整代码
-
堆排序(补)
- 描述
- 代码实现
堆的基本概念
二叉堆
什么是堆?
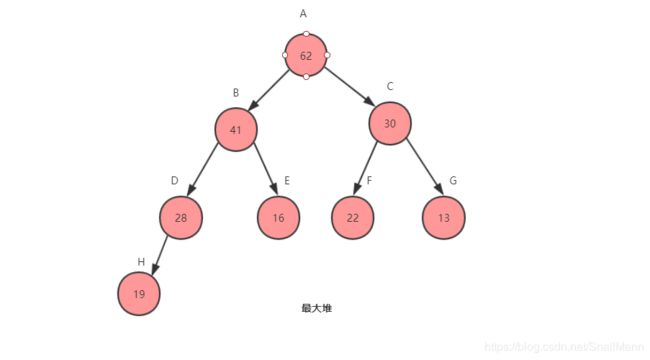
通常我们所说的堆,就是二叉树的一种变形,所以它本质也是一棵二叉树,只不过有一些自己的特点,所以我们有叫堆为二叉堆
- 堆,也叫二叉堆,它是一棵完全二叉树
- 堆的每棵子树都是一个堆
- 堆可以分为最大堆和最小堆
- 堆中的元素必须可以比较
堆的常用场景:
- 构建优先队列(可以参考Java的优先队列
PriorityQueue) - 支持堆排序
- 快速找出一个集合中的最小值(或者最大值)
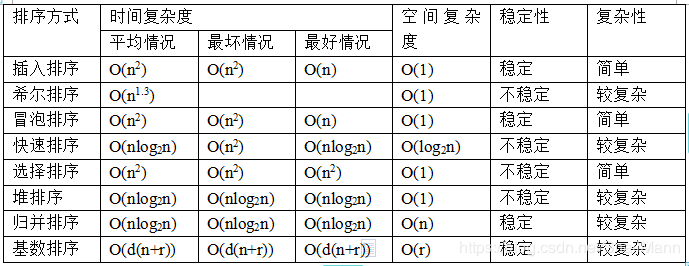
比如我们要实现一个优先队列的时候,通常会以下几种底层数据结构
| 数据结构 | 入队 | 出队 |
|---|---|---|
| 普通线性结构 | O(1)[顺序入队] | O(n)[每次都求优先级最高,类似求最大值] |
| 顺序线性结构 | O(n)[入队,每次都找到插入的位置] | O(1) [因为已经排好序,直接取优先级最高] |
| 堆 | O(logn) | O(logn) |
最大堆和最小堆
堆分为两种:
最大堆(大根堆)
在最大堆中,父结点的值比所有子结点的值都要大(或相等)最小堆(小根堆)
在最小堆中,父结点的值要比所有子结点的值要小(或相等)
注意点
- 从最大堆的特性中,我们知道,父结点的值一定是大于等于孩子结点的值,那么如果有一个最大堆的高是
3,排除根结点,高层级的结点一定是大于低层级结点的值吗? 这个是不一定的,我们可以看到上面图中的最大堆,第三层的结点E的值就比第四层结点H的值要小。
最大堆
实现基础
我们通常说的堆数据结构,就是二叉堆,本质上是一棵完全二叉树;通常在代码的实现中,二叉堆的底层数据结构是使用数组而不是二叉链,因为如果使用数组,二叉堆可以存在以下特性:
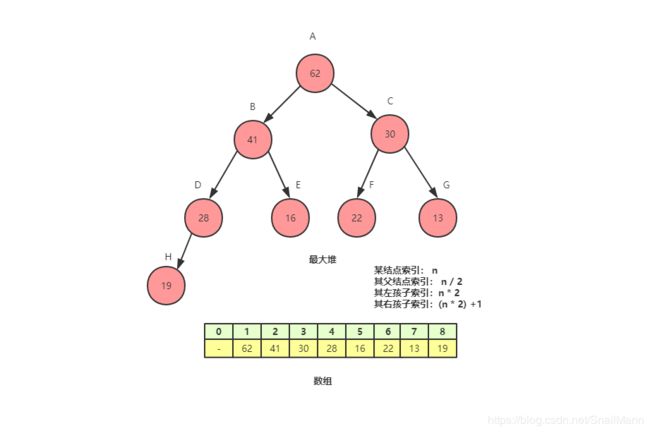
如果我们以数组来存储堆的结点元素,从数组的第二个索引1开始存储,堆中的取任意结点,索引为n, 那么可以满足:
- 父结点索引为
n / 2 - 左孩子索引为
2 * n - 右孩子索引为
(2 * n) + 1
为什么要从数组的第二个位置,索引1开始存放元素呢?因为很多的教材就是从索引开始存放的,公式也简单好记。只不过在我们自己实现代码时,可能就要多注意一下地方。
在我们了解堆使用数组存储的特性后,为了让代码更简洁高效,我们要从数组第一个位置开始存储,即索引为0的地方也存放元素,优化一下,所以规律就变成了
- 父结点索引为
(n-1)/2 - 左孩子索引为
2*n + 1 - 右孩子索引为
(2*n + 1) + 1=2*n + 2
仅仅是没这么好记了罢了,不过代码上的实现就简单了,下面我们就来实现一个二叉堆的最大堆, 最小堆差不多的啦,就反过来而已。
动态数组
这里我们主要是实现堆,所以不想考虑过多的数组细节,就复制了网上的一份动态数组的实现源码,感觉就类似ArrayList吧,用来代替数组成为二叉堆的
/**
* 动态数据
*
* @param
*/
public class Array<E> {
private E[] data;
private int size;
public Array(int capacity) { // user assign size
data = (E[]) new Object[capacity];
size = 0;
}
public Array() {
this(10); // default size
}
public Array(E[] arr) {
data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
size = arr.length;
}
public int getSize() {
return size;
}
public int getCapacity() {
return data.length;
}
public boolean isEmpty() {
return size == 0;
}
public void rangeCheck(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Index is Illegal!");
}
}
public void add(int index, E e) {
if (index < 0 || index > size) {
throw new IllegalArgumentException("Index is Illegal ! ");
}
if (size == data.length) {
resize(data.length * 2);
}
for (int i = size - 1; i >= index; i--) {
data[i + 1] = data[i];
}
data[index] = e;
size++;
}
private void resize(int newCapacity) {
E[] newData = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newData[i] = data[i];
}
data = newData;
}
public void addLast(E e) { //末尾添加
add(size, e);
}
public void addFirst(E e) { //头部添加
add(0, e);
}
public E get(int index) {
rangeCheck(index);
return data[index];
}
public E getLast() {
return get(size - 1);
}
public E getFirst() {
return get(0);
}
public void set(int index, E e) {
rangeCheck(index);
data[index] = e;
}
public boolean contains(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e)) {
return true;
}
}
return false;
}
public int find(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e)) {
return i;
}
}
return -1;
}
public E remove(int index) { // remove data[index] and return the value
rangeCheck(index);
E res = data[index];
for (int i = index; i < size - 1; i++) {
data[i] = data[i + 1];
}
size--;
data[size] = null;//loitering objects != memory leak
if (size == data.length / 4 && data.length / 2 != 0) {
resize(data.length / 2); //防止复杂度的震荡
}
return res;
}
public E removeFirst() {
return remove(0);
}
public E removeLast() {
return remove(size - 1);
}
public void removeElement(E e) { //only remove one(may repetition) and user not know whether is deleted.
int index = find(e);
if (index != -1) {
remove(index);
}
}
// new method
public void swap(int i, int j) {
if (i < 0 || i >= size || j < 0 || j >= size) {
throw new IllegalArgumentException("Index is illegal.");
}
E t = data[i];
data[i] = data[j];
data[j] = t;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append(String.format("Array : size = %d, capacity = %d\n", size, data.length));
res.append("[");
for (int i = 0; i < size; i++) {
res.append(data[i]);
if (i != size - 1) {
res.append(", ");
}
}
res.append("]");
return res.toString();
}
}
- 用于代替数组
上浮 shift up
- 新添加的元素放到数组末尾
- 判断新添加的元素与其父结点的大小,如果新添元素大于其父结点,则上浮
- 直到新添元素小于其父结点值,或新添元素已经上浮到根结点位置

/**
* index索引的元素执行上浮操作
*
* @param index
*/
private void siftUp(int index) {
//index不可以是根节点,所以必须>0 ,且上浮结点的值必须大于其父节点的值,只要满足条件,一直上浮
while (index > 0 && array.get(index).compareTo(array.get(parent(index))) > 0) {
//交换位置
array.swap(index, parent(index));
//下一个
index = parent(index);
}
}
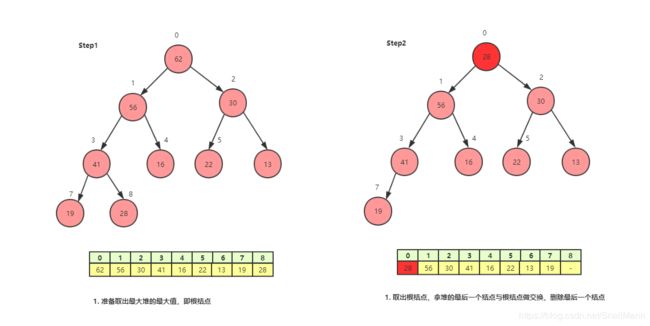
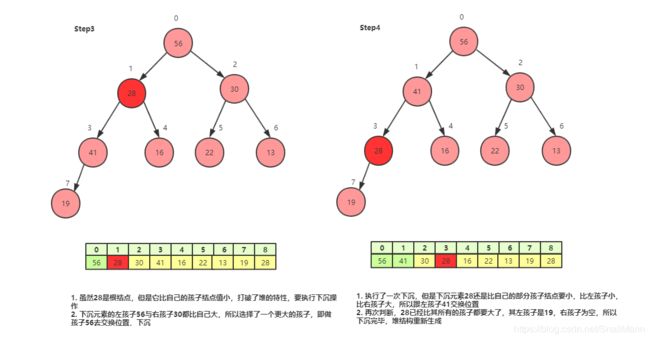
下沉 shift down
- 首先判断下沉元素的孩子结点,看是左孩子大还是右孩子大?取最大的那个孩子与下沉结点比较,如果下沉元素比最大孩子的值还要大,就不需要下沉,已经满足最大堆特性
- 如果下沉元素比最大孩子小,则交换位置。
- 不断重复判断是否执行下沉操作,直到下沉元素比孩子结点的值大或者下沉元素已经是叶子结点
/**
* 对索引为index的元素进行下沉操作
*
* @param index
*/
private void siftDown(int index) {
/**
* 下沉同样是一个循环,只要不是叶子结点不断循环
* 1. 只要下沉元素的左孩子的索引小于等于数组的最大索引,就代表下沉元素还不是叶子结点,还可以循环
*/
while (lchild(index) <= array.getSize() - 1) {
/**
* 1. 求左右孩子谁的值大,就取谁的索引
*/
//获得左右孩子索引
int lIndex = lchild(index);
int rIndex = rchild(index);
int max = 0;
//求最大
//如果其右孩子索引大于数组的最大索引,则越界,不存在右孩子 | while循环已经保证了肯定有左孩子 |右孩子索引没有越界,就代表有右孩子
if (rIndex > array.getSize() - 1) {
max = lIndex;
//如果有右孩子,则比较左右孩子的大小,取最大的孩子的索引
} else {
max = array.get(lIndex).compareTo(array.get(rIndex)) > 0 ? lIndex : rIndex;
}
/**
* 下沉元素与最大孩子结点比较
* 1. 如果下沉元素比最大的孩子结点都要大,那么这就代表下沉已经结束,堆结构特性已经满足
*/
if (array.get(index).compareTo(array.get(max)) >= 0) {
break;
}
//如果下沉元素没有最大孩子结点大,则交换位置,继续下沉
array.swap(index, max);
//下一个
index = max;
}
}
添加元素 add
- 时间复杂度O(logn)
- 追加元素到数组尾部
- 对新添元素进行上浮操作,直到满足最大堆特性
/**
* 给堆添加一个元素
*
* @param data
*/
public void add(T data) {
//动态数组中追加元素
array.addLast(data);
//新添元素执行上浮操作,传入新添元素的索引,即最后一个位置
siftUp(array.getSize() - 1);
}
取最大值 extractMax
- 时间复杂度O(logn)
- 取出最大值,把堆中(数组)最后的元素与根结点交换位置,删除最后的元素
- 对交换后的根结点元素进行下沉操作,直到满足最大堆特性
/**
* 取出堆中的最大值
*
* @return
*/
public T extractMax() {
//找到最大值
T max = array.get(0);
//最后元素和根结点交换位置
array.swap(0, array.getSize() - 1);
//删除最后的元素
array.removeLast();
//下沉操作
siftDown(0);
return max;
}
取最大值,并插入新元素 replace
- 原思想,extractMax + add 两个O(logn)操作
- 但是,我们直接把要插入的元素替换到根结点位置,再下沉,就只需要一个O(logn)了
/**
* 取出最大元素,同时插入一个新元素
* 原思想,extractMax + add 两个O(logn)操作
* 但是,我们直接把要插入的元素替换到根结点位置,再下沉,就只需要一个O(logn)了
*
* @param data
* @return
*/
public T replace(T data) {
//获得最大值
T max = array.get(0);
//根结点替换为新元素
array.set(0, data);
//对新元素进行下沉
siftDown(0);
return max;
}
将任意数组堆化 heapify
重点步骤:
- 先找到堆的第一个非叶子节点(方式可以通过找到最后一个结点,它的父结点,就是第一个非叶子结点)
- 所有非叶子结点,逐一下沉,直到根结点也完成下沉,就是整棵完全二叉树堆化完成
好处:
- 将n各元素逐个插入到一个空堆中,时间复杂度是O(nlogn)
- heapify的时间复杂度是O(n), 推算比较复杂,这里记住就好
/**
* 实现构造方法中
* 将数组堆化,heapify过程
*
* @param array
*/
public MaxHeap(T[] array) {
this.array = new Array<>(array);
/**
* heapify过程
* 1. i 初始化为 第一个非叶子结点的索引,通过最后一个元素的父结点的方式确定
* 2. i之后每次减1,就是上一个非叶子结点,直到根结点也完成下沉化
* 3. 最后完成堆化
*/
for (int i = parent(array.length - 1); i >= 0; i--) {
siftDown(i);
}
}
Java代码实现
描述
- 以动态数组为底层数据结构
- 从数组的第一个位置,即索引为0的地方开始存放元素
- 最大堆
- 堆内元素必须可以比较,即实现了Comparable接口
实现功能
- 上浮 shift up;
- 下沉 shift down
- 添加元素 add
- 取最大值 extractMax
- 取最大值,同时插入新元素 replace
- 将任意数组堆化 heapify
完整代码
动态数组
package com.snailmann.datastructure.heap;
/**
* 动态数据
*
* @param
*/
public class Array<E> {
private E[] data;
private int size;
public Array(int capacity) { // user assign size
data = (E[]) new Object[capacity];
size = 0;
}
public Array() {
this(10); // default size
}
public Array(E[] arr) {
data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
size = arr.length;
}
public int getSize() {
return size;
}
public int getCapacity() {
return data.length;
}
public boolean isEmpty() {
return size == 0;
}
public void rangeCheck(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Index is Illegal!");
}
}
public void add(int index, E e) {
if (index < 0 || index > size) {
throw new IllegalArgumentException("Index is Illegal ! ");
}
if (size == data.length) {
resize(data.length * 2);
}
for (int i = size - 1; i >= index; i--) {
data[i + 1] = data[i];
}
data[index] = e;
size++;
}
private void resize(int newCapacity) {
E[] newData = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newData[i] = data[i];
}
data = newData;
}
public void addLast(E e) { //末尾添加
add(size, e);
}
public void addFirst(E e) { //头部添加
add(0, e);
}
public E get(int index) {
rangeCheck(index);
return data[index];
}
public E getLast() {
return get(size - 1);
}
public E getFirst() {
return get(0);
}
public void set(int index, E e) {
rangeCheck(index);
data[index] = e;
}
public boolean contains(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e)) {
return true;
}
}
return false;
}
public int find(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e)) {
return i;
}
}
return -1;
}
public E remove(int index) { // remove data[index] and return the value
rangeCheck(index);
E res = data[index];
for (int i = index; i < size - 1; i++) {
data[i] = data[i + 1];
}
size--;
data[size] = null;//loitering objects != memory leak
if (size == data.length / 4 && data.length / 2 != 0) {
resize(data.length / 2); //防止复杂度的震荡
}
return res;
}
public E removeFirst() {
return remove(0);
}
public E removeLast() {
return remove(size - 1);
}
public void removeElement(E e) { //only remove one(may repetition) and user not know whether is deleted.
int index = find(e);
if (index != -1) {
remove(index);
}
}
// new method
public void swap(int i, int j) {
if (i < 0 || i >= size || j < 0 || j >= size) {
throw new IllegalArgumentException("Index is illegal.");
}
E t = data[i];
data[i] = data[j];
data[j] = t;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append(String.format("Array : size = %d, capacity = %d\n", size, data.length));
res.append("[");
for (int i = 0; i < size; i++) {
res.append(data[i]);
if (i != size - 1) {
res.append(", ");
}
}
res.append("]");
return res.toString();
}
}
最大堆:
package com.snailmann.datastructure.heap;
import java.util.Arrays;
import java.util.Random;
/**
* 最大堆 | 采用动态数组结构
* 从索引为0的地方开始存储,动态数组
* 最大堆元素必须可以比较,即实现Comparable接口
* 父结点: (n - 1)/ 2
* 左孩子: 2 * n + 1
* 右孩子: 2 * n + 2
*
* @param
*/
public class MaxHeap<T extends Comparable<T>> {
/**
* 底层数据结构 | 动态数组
*/
private Array<T> array;
public MaxHeap() {
this.array = new Array<>();
}
/**
* 将数组堆化,heapify过程
*
* @param array
*/
public MaxHeap(T[] array) {
this.array = new Array<>(array);
//heapify
heapify(array);
}
/**
* heapify过程 | 最大堆
* 1. i 初始化为 第一个非叶子结点的索引,通过最后一个元素的父结点的方式确定
* 2. i之后每次减1,就是上一个非叶子结点,直到根结点也完成下沉化
* 3. 最后完成堆化
*
* @param array
*/
public void heapify(T[] array) {
for (int i = parent(array.length - 1); i >= 0; i--) {
siftDown(i);
}
}
/**
* 返回堆的元素个数
*
* @return
*/
public int size() {
return array.getSize();
}
/**
* 堆是否为空
*
* @return
*/
public boolean isEmpty() {
return array.isEmpty();
}
/**
* 获取某个结点的父结点索引
*
* @param index
* @return
*/
private int parent(int index) {
if (index == 0) {
throw new RuntimeException("根结点没有父结点");
}
return (index - 1) / 2;
}
/**
* 获取某个结点的左孩子索引
*
* @param index
* @return
*/
private int lchild(int index) {
return (2 * index) + 1;
}
/**
* 获取某个结点的右孩子索引
*
* @param index
* @return
*/
private int rchild(int index) {
return (2 * index) + 2;
}
/**
* 给堆添加一个元素 | 时间复杂度O(logn)
*
* @param data
*/
public void add(T data) {
//动态数组中追加元素
array.addLast(data);
//新添元素执行上浮操作,传入新添元素的索引,即最后一个位置
siftUp(array.getSize() - 1);
}
/**
* index索引的元素执行上浮操作
*
* @param index
*/
private void siftUp(int index) {
//index不可以是根节点,所以必须>0 ,且上浮结点的值必须大于其父节点的值,只要满足条件,一直上浮
while (index > 0 && array.get(index).compareTo(array.get(parent(index))) > 0) {
//交换位置
array.swap(index, parent(index));
//下一个
index = parent(index);
}
}
/**
* 取出堆中的最大值 | 时间复杂度O(logn)
*
* @return
*/
public T extractMax() {
//找到最大值
T max = array.get(0);
//最后元素和根结点交换位置
array.swap(0, array.getSize() - 1);
//删除最后的元素
array.removeLast();
//下沉操作
siftDown(0);
return max;
}
/**
* 对索引为index的元素进行下沉操作
*
* @param index
*/
private void siftDown(int index) {
/**
* 下沉同样是一个循环,只要不是叶子结点不断循环
* 1. 只要下沉元素的左孩子的索引小于等于数组的最大索引,就代表下沉元素还不是叶子结点,还可以循环
*/
while (lchild(index) <= array.getSize() - 1) {
/**
* 1. 求左右孩子谁的值大,就取谁的索引
*/
//获得左右孩子索引
int lIndex = lchild(index);
int rIndex = rchild(index);
int max = 0;
//求最大
//如果其右孩子索引大于数组的最大索引,则越界,不存在右孩子 | while循环已经保证了肯定有左孩子 |右孩子索引没有越界,就代表有右孩子
if (rIndex > array.getSize() - 1) {
max = lIndex;
//如果有右孩子,则比较左右孩子的大小,取最大的孩子的索引
} else {
max = array.get(lIndex).compareTo(array.get(rIndex)) > 0 ? lIndex : rIndex;
}
/**
* 下沉元素与最大孩子结点比较
* 1. 如果下沉元素比最大的孩子结点都要大,那么这就代表下沉已经结束,堆结构特性已经满足
*/
if (array.get(index).compareTo(array.get(max)) >= 0) {
break;
}
//如果下沉元素没有最大孩子结点大,则交换位置,继续下沉
array.swap(index, max);
//下一个
index = max;
}
}
/**
* 取出最大元素,同时插入一个新元素
* 原思想,extractMax + add 两个O(logn)操作
* 但是,我们直接把要插入的元素替换到根结点位置,再下沉,就只需要一个O(logn)了
*
* @param data
* @return
*/
public T replace(T data) {
//获得最大值
T max = array.get(0);
//根结点替换为新元素
array.set(0, data);
//对新元素进行下沉
siftDown(0);
return max;
}
public static void main(String[] args) {
int len = 100;
Random random = new Random();
MaxHeap<Integer> maxHeap = new MaxHeap<>();
for (int i = 0; i < len; i++) {
maxHeap.add(random.nextInt(100));
}
int[] arr = new int[len];
for (int i = 0; i < len; i++) {
arr[i] = maxHeap.extractMax();
}
System.out.println(Arrays.toString(arr));
}
}
- 同一个无序数组,通过一个一个add出来的堆结构和heapify出来的堆结构,实际的结点位置是会有偏差的,不过都满足堆的特性
堆排序
描述
什么是堆排?
本来这里主要是讲一下堆的结构和实现,但是其实堆排序其实也是一个挺重要的数据结构知识,毕竟属于基本的八大排序之一嘛,所以这里就再补充一些堆排的知识
我们知道,堆的底层结构就是一个数组,所以我们就可以利用这个数组同时是堆的底层结构的特性,利用堆的特性,对这个数组进行排序,得到一个有序数组。 利用堆的特性对底层无序数组排序的过程就是堆排
堆排的特性:
堆排不跟其他排序算法一样,不依赖什么东西,堆排的实现非常的依赖堆这个数据结构,所以无堆则无堆排,所以如果我们要对一个无序数组进行排序,首先就要将该无序数组构造成一个最大堆或最小堆,不同种的堆也会造成不同的顺序排序
最大堆堆排后的结果是升序序列最小堆堆排后的结果是降序序列
堆排的时间复杂度是:
基本思想和实现步骤
- 图解排序算法(三)之堆排序 - @作者:dreamcatcher-cx
堆排是对一个无序数组堆化,再排的过程,所以它的核心思想就是:
- 看无序数组是想进行什么排序?升序还是降序?
- 如果升序,就先将无序数组堆化成最大堆,反之则最小堆。通过heapify去实现
- 堆化后,将堆顶元素与末尾元素交换,堆的结点长度减1,对当前堆进行重建,下沉,直到重新满足堆特性
- 遍历堆中未交换过的结点,遍历交换完毕后,就是数组排序的结束
代码实现
package com.snailmann.datastructure.heap;
/**
* 堆排 | 升序 |O(nlogn)
* 最大堆 -> 升序排序
*
* @param
*/
public class MaxHeapSort<T extends Comparable<T>> {
/**
* 底层数据结构 | 动态数组
*/
private Array<T> array;
public MaxHeapSort() {
this.array = new Array<>();
}
/**
* heapify过程 | 最大堆
* 1. i 初始化为 第一个非叶子结点的索引,通过最后一个元素的父结点的方式确定
* 2. i之后每次减1,就是上一个非叶子结点,直到根结点也完成下沉化
* 3. 最后完成堆化
*
* @param array
*/
public void heapify(T[] array) {
for (int i = parent(array.length - 1); i >= 0; i--) {
siftDown(i, array.length);
}
}
/**
* 获取某个结点的父结点索引
*
* @param index
* @return
*/
private int parent(int index) {
if (index == 0) {
throw new RuntimeException("根结点没有父结点");
}
return (index - 1) / 2;
}
/**
* 获取某个结点的左孩子索引
*
* @param index
* @return
*/
private int lchild(int index) {
return (2 * index) + 1;
}
/**
* 获取某个结点的右孩子索引
*
* @param index
* @return
*/
private int rchild(int index) {
return (2 * index) + 2;
}
/**
* 对索引为index的元素进行下沉操作
*
* @param index 下沉元素索引
* @param len 要重建的堆的结点个数
*/
private void siftDown(int index, int len) {
/**
* 下沉同样是一个循环,只要不是叶子结点不断循环
* 1. 只要下沉元素的左孩子的索引小于整个数组的长度,就代表下沉元素还不是叶子结点,还可以循环
*/
while (lchild(index) <= len - 1) {
/**
* 1. 求左右孩子谁的值大,就取谁的索引
*/
//获得左右孩子索引
int lIndex = lchild(index);
int rIndex = rchild(index);
int max = 0;
//求最大
//如果其右孩子索引大于数组的最大索引,则越界,不存在右孩子 | while循环已经保证了肯定有左孩子 |右孩子索引没有越界,就代表有右孩子
if (rIndex > len - 1) {
max = lIndex;
//如果有右孩子,则比较左右孩子的大小,取最大的孩子的索引
} else {
max = array.get(lIndex).compareTo(array.get(rIndex)) > 0 ? lIndex : rIndex;
}
/**
* 下沉元素与最大孩子结点比较
* 1. 如果下沉元素比最大的孩子结点都要大,那么这就代表下沉已经结束,堆结构特性已经满足
*/
if (array.get(index).compareTo(array.get(max)) >= 0) {
break;
}
//如果下沉元素没有最大孩子结点大,则交换位置,继续下沉
array.swap(index, max);
//下一个
index = max;
}
}
/**
* 堆排序 | 最大堆 -> 升序 | 时间复杂度O(nlogn)
* 1. 把无序数组堆化,构建二叉堆
* 2. 将堆顶元素与末尾元素交换,循环下沉直至重新满足最大堆结构,待所有元素都交换完毕后,排序完成
*
* @param arary
*/
public void heapSort(T[] arary) {
//将无序数组构建成一个最大堆
this.array = new Array<>(arary);
heapify(arary);
System.out.println(this.array.toString());
//循环交换,重建的过程
for (int i = this.array.getSize() - 1; i > 0; i--) {
//交换位置
this.array.swap(0, i);
//每交换一次,实际的堆结构减少一个长度,因为交换到尾部的大数值,已经排序完毕
int len = i - 1;
//重建,下沉
siftDown(0, len);
}
System.out.println(this.array.toString());
}
@Override
public String toString() {
return this.array.toString();
}
public static void main(String[] args) {
Integer[] nums = new Integer[]{3, 4, 1, 3, 0, 4, 7, 9};
MaxHeapSort<Integer> maxHeapSort = new MaxHeapSort<>();
maxHeapSort.heapSort(nums);
}
}
参考资料
- 数据结构:堆(Heap)- @作者:唐先僧
- ZXZxin/ZXBlog/优先队列和堆的总结 - @作者:ZXZxin
- 图解排序算法(三)之堆排序 - @作者:dreamcatcher-cx
- 如果觉得对你有帮助,能否点个赞或关个注,以示鼓励笔者呢?!