最短路径问题
一.迪克斯特朗算法
from IPython.display import Image
Image(filename="./data/9_01.png",width=800,height=960)

Image(filename="./data/9_02.png",width=800,height=960)
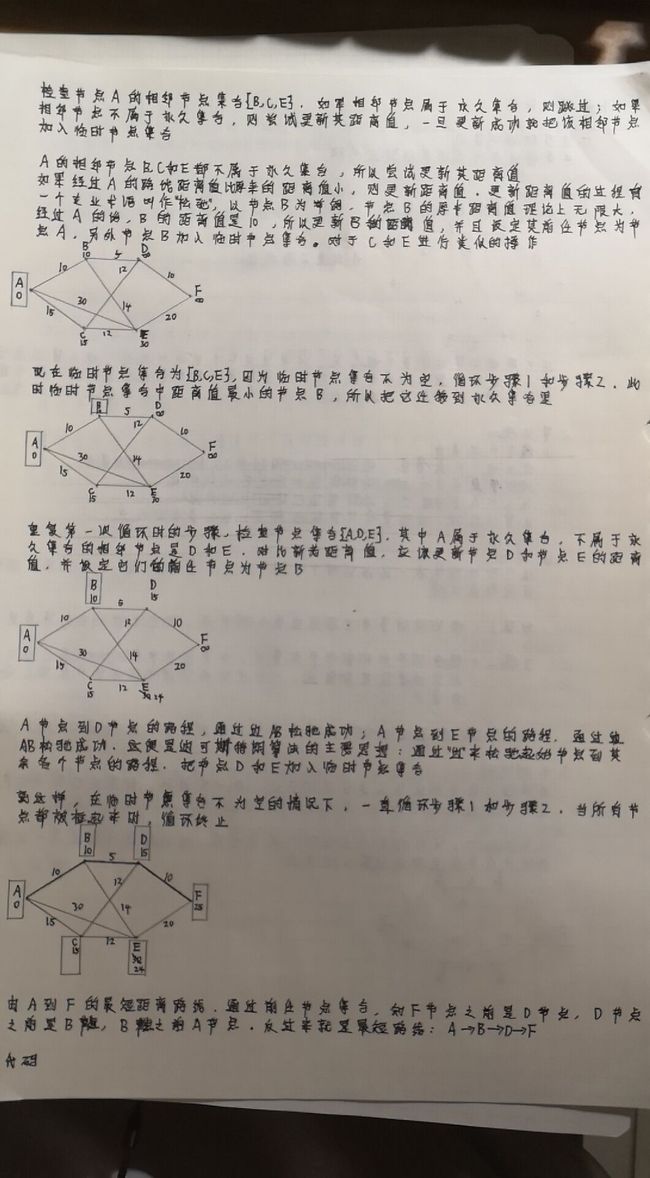
from collections import defaultdict
import sys
class Graph(object):
def __init__(self):
self.nodes=set()
self.edges=defaultdict(list)
self.distances={}
def add_node(self,node):
self.nodes.add(node)
def add_edge(self,from_node,to_node,distance):
self.edges[from_node].append(to_node)
self.distances[(from_node,to_node)]=distance
class Node(object):
def __init__(self,name):
self.distance=sys.maxsize
self.predecessor=None
self.name=name
def set_distance(self,dist):
self.distance=dist
def set_predecessor(self,pred):
self.predecessor=pred
def get_distance(self):
return self.distance
def get_predecessor(self):
return self.predecessor
g=Graph()
g.add_node(Node("A"))
g.add_node(Node("B"))
g.add_node(Node("C"))
g.add_node(Node("D"))
g.add_node(Node("E"))
g.add_node(Node("F"))
g.add_edge("A","B",10)
g.add_edge("B","A",10)
g.add_edge("A","C",15)
g.add_edge("C","A",15)
g.add_edge("A","E",30)
g.add_edge("E","A",30)
g.add_edge("B","D",5)
g.add_edge("D","B",5)
g.add_edge("B","E",14)
g.add_edge("E","B",14)
g.add_edge("C","D",12)
g.add_edge("D","C",12)
g.add_edge("C","E",12)
g.add_edge("E","C",12)
g.add_edge("D","F",10)
g.add_edge("F","D",10)
g.add_edge("E","F",20)
g.add_edge("F","E",20)
permanent=set()
temporary=set()
temporary.add(initial)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
in
2 temporary=set()
3
----> 4 temporary.add(initial)
NameError: name 'initial' is not defined
while temporary:
min_node=None
for node in temporary:
if min_node is None:
min_node=node
elif node.get_distance()<min_node.get_distance():
min_node=node
temporary.remove(min_node)
permanent.add(min_node)
current_distance=min_node.get_distance()
for neighbour in graph.edges[min_node]:
new_distance=current_distance+graph.distance[(min_node,neighbour)]
if neighbour not in permanent and new_distance<neighbour.get_distance():
neighbour.set_distance(new_distance)
neighbour.set_predecessor(min_node)
temporary.add(neighbour)
def printPath(self,end,predecessor):
current=end
path={end}
while current.predecessor!=None:
path.add(current.predecessor)
current=current.predecessor
path.reverse()
print(path)
完整代码
from collections import defaultdict
import sys
class Graph(object):
def __init__(self):
self.nodes=set()
self.edges=defaultdict(list)
self.distances={}
def add_node(self,node):
self.nodes.add(node)
def add_edge(self,from_node,to_node,distance):
self.edges[from_node].append(to_node)
self.distances[(from_node,to_node)]=distance
class Node(object):
def __init__(self,name):
self.distance=sys.maxsize
self.predecessor=None
self.name=name
def set_distance(self,dist):
self.distance=dist
def set_predecessor(self,pred):
self.predecessor=pred
def get_distance(self):
return self.distance
def get_predecessor(self):
return self.predecessor
def dijsktra(graph,initial,end):
permanent={}
temporary={}
temporary.add(initial)
initial.set_distance(0)
while temporary:
min_node=None
for node in temporary:
if min_node is None:
min_node=node
elif node.get_distance()<min_node.get_distance():
min_node=node
temporary.remove(min_node)
permanent.add(min_node)
current_distance=min_node.get_distance()
for neighbour in graph.edges[min_node]:
new_distance=current_distance+graph.distance[(min_node,neighbour)]
if neighbour not in permanent and new_distance<neighbour.get_distance():
neighbour.set_distance(new_distance)
neighbour.set_predecessor(min_node)
temporary.add(neighbour)
def printPath(self,end,predecessor):
current=end
path={end}
while current.predecessor!=None:
path.add(current.predecessor)
current=current.predecessor
path.reverse()
print(path)
二.Floyd算法
Image(filename="./data/9_03.png",width=800,height=960)

Image(filename="./data/9_04.png",width=800,height=960)

import sys
class Floyd(object):
def __init__(self):
pass
def solveFloyd(self,dist,start,end):
n=len(dist)
path=self.createPath(n)
for k in range(n):
for i in range(n):
for j in range(n):
if dist[i][j]>dist[i][k]+dist[k][j]:
dist[i][j]=dist[i][k]+dist[k][j]
path[i][j]=path[i][k]
self.printPath(start,path,end)
def createPath(self,n):
path=[]
for i in range(n):
row=[]
for j in range(n):
row.append(j)
path.append(row)
return path
def printPath(self,current,path,end):
solution=[]
while current!=end:
solution.append(current)
current=path[current][end]
solution.append(current)
print(solution)
dist=[
[0,10,15,sys.maxsize,30,sys.maxsize],
[10,0,sys.maxsize,5,14,sys.maxsize],
[15,sys.maxsize,0,12,12,sys.maxsize],
[sys.maxsize,5,12,0,sys.maxsize,10],
[30,14,12,sys.maxsize,0,20],
[sys.maxsize,sys.maxsize,sys.maxsize,10,20,0]
]
Floyd().solveFloyd(dist,0,5)
[0, 1, 3, 5]
三.A*算法
Image(filename="./data/9_05.png",width=800,height=960)





