HDU 6158 笛卡尔定理 + 韦达定理
题目链接
感谢ICPCCamp的题解,链接送上:CCPC 2017网络赛题解
题解已经讲得非常清楚了,补充一点细节吧。
(1).关于笛卡尔定理
对于此题,只需要了解这么一个性质:(来自wiki 用的谷歌翻译,若有偏差还请指出~)
定义一个圆的曲率 k = ± 1 r k =\pm \frac{1}{r} k=±r1,其中 r r r是其半径。
若平面有两两相切,且有 6 6 6个独立切点的四个圆,设其曲率为 k 1 , k 2 , k 3 , k 4 k_1,k_2,k_3,k_4 k1,k2,k3,k4(若该圆与其他圆均外切,则曲率取正,否则取负)则其满足性质:
( k 1 + k 2 + k 3 + k 4 ) 2 = 2 ( k 1 2 + k 2 2 + k 3 2 + k 4 2 ) (k_1 + k_2 + k_3 + k_4)^2 =2 (k_1^2 +k_2^2+k_3^2 + k_4^2 ) (k1+k2+k3+k4)2=2(k12+k22+k32+k42)
(2).关于韦达定理
对于此题,第一个与已知圆相切的圆的半径非常好求,其半径 r 3 = ( r 1 − r 2 ) r_3 = (r_1 - r_2) r3=(r1−r2),其中 r 1 r_1 r1是已知圆中较大圆的半径。
故我们现在 k 1 , k 2 , k 3 k_1,k_2,k_3 k1,k2,k3均为已知,代入上面笛卡尔定理的式子便能求解出 k 4 k_4 k4。
易发现这是一个关于 k 4 k_4 k4的二次方程,化简为标准形式为:
k 4 2 − 2 ( k 1 + k 2 + k 3 ) k 4 + ( k 1 + k 2 + k 3 ) 2 − 2 ( k 1 2 + k 2 2 + k 3 2 ) = 0 k_4^2 - 2(k_1+k_2+k_3)k_4 + (k1+k2+k3)^2 - 2(k_1^2+k_2^2+k_3^2) = 0 k42−2(k1+k2+k3)k4+(k1+k2+k3)2−2(k12+k22+k32)=0
直接求解是挺困难的,设两个解是 x 1 , x 2 x_1,x_2 x1,x2,利用韦达定理:
x 1 + x 2 = 2 ( k 1 + k 2 + k 3 ) x_1 + x_2 = 2(k1 + k2 + k3) x1+x2=2(k1+k2+k3)
因为 k 4 k_4 k4所代表的圆与前三个圆均相切,对于此题, x 1 , x 2 x_1,x_2 x1,x2就是 k 3 k_3 k3所代表圆左右两个圆的曲率。
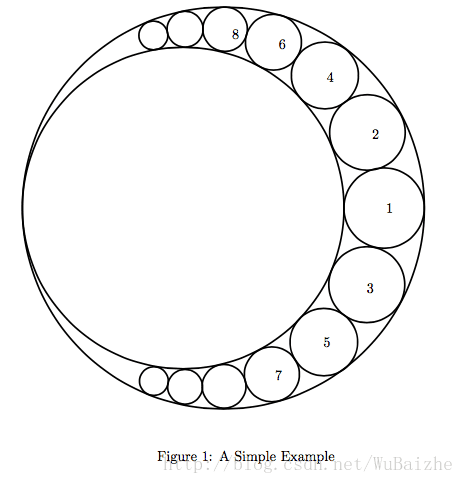
对于题目给的图:
若 k 3 k_3 k3代表圆 1 1 1,则 x 1 , x 2 x_1,x_2 x1,x2分别代表圆2和圆3
若 k 3 k_3 k3代表圆 2 2 2,则 x 1 , x 2 x_1,x_2 x1,x2分别代表圆1和圆4
这样我们就可以类似迭代的方式,不断往后递推求解。
另外小心精度和时间的问题。
因为N越大,其后面的圆的面积对于答案的贡献几乎可以忽略不计,这时要及时退出循环,避免超时。
亲测,当eps取(1e-13)时跑得最快。
218msAC
代码:
#include