matlab中用polyfit、regress、nlinfit等进行详细的回归分析

1.说明

1. 该学习笔记仅供个人学习使用，不代表任何官方指导或意见。
2. 该学习笔记为个人原创，转载请征得博主同意，或声明原文链接。
3. 继我上一次写的学习笔记数据探索、数据清洗学习笔记与用matlab代码进行数据探索、数据清洗学习笔记，回归的部分
4. 有需要其他资料或有其他问题可私信或者加qq2356081476，这不是我的义务但也欢迎各位朋友与我讨论相关问题，共同进步。
5. 错字，语法，排版等问题请见谅。
6. 版权问题我不太懂，有侵权等问题请联系我。
7. 好多不懂的代码一定要自己跟着试，看着资料一步一步试。我在学习的时候也是很多不懂的，拿着matlab r2018b一起试着会了的。

2.回归的介绍

对小白说，根据点（数据）的趋势，用线表示出来这个趋势。
专业点说，数据拟合。

这条线是什么样子的，直线的？曲线的？

• 直线的我们叫线性回归。
• 曲线的我们叫非线性回归，或者一个更通俗的名字曲线回归。

还有其他的没有说明，这篇先会介绍这两个并介绍matlab的代码。

2-1.前面两篇所发现的一些问题

2-1-1.回归和拟合是什么关系？

就我所查，拟合包括回归，插值，逼近。后两个不介绍了，关系就是拟合有多种方法，其中包括回归。所以有老板叫你做数据拟合去的时候，你要知道，就是要你去回归，要你去求出数据的趋势。

2-1-2.回归到底是做预测还是用来去脏数据？

没查到资料详细介绍这个问题
与一些其他资料所冲突的是我个人意见，不能预测，只能用来去脏数据。他们说可以预测，我说不能，为什么？最后所求得的线拟合数据拟合得很好，但不是数据的那一段线可能会有很严重的偏差。看一个图。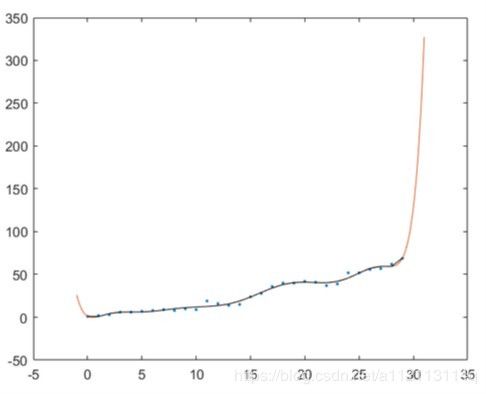
这个是我用一元十次多项式拟合数据（蓝色的是数据点），在没有数据点的两边极速上升，非常不符合数据缓慢上升的趋势。

3.三个函数的核心：最小二乘法

3-1.介绍

先把公式写出来再说怎么来的：
$$D=\sum _{i=1}^n{d}_i^2=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$
其中
$y_i$是数据点的y值（在横坐标$x_i$处的纵坐标值）
${\hat{y}}_i$是我们拟合的线在横坐标$x_i$处的纵坐标值。
当D最小时，求得的 ${\hat{y}}_i$就是我们要的。

怎么求：
并且因为有平方，所以有最小值。在数学上求导为零的地方在实际意义上是那个最小值点，所以求导，解出来。

通俗理解还可以参考下面两篇个人觉得很好的文章：
https://blog.csdn.net/ReCclay/article/details/82914109
https://blog.csdn.net/alw_123/article/details/82193535

3-2.matlab代码

代码中会用到正规方程解，及：
$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$
这里我们先晓得怎么用就好，想要了解可以参考：
https://blog.csdn.net/alw_123/article/details/82825785
X的形式比较特殊。

clc;
clear;

%录入X轴数据
for a = 1:30
    x(a) = a-1;
end

%录入Y轴数据
y=[1,2,3,6,6,7,8,9,8,10,9,19,16,14,15,24,28,36,40,40,42,41,37,39,52,52,56,57,62,69];
plot(x,y,'.');		%画点
hold on

k=10;			%阶数  阶数可以更改看效果，

%X矩阵的形式
for a = 0:k
    for i = 1:30
        X(i,(a+1)) = x(i).^(a);
    end
end

Y = y';
A = (X'*X)^-1*X'*Y;	%这个A就是上面我们说的正规方程解
A = A';			%转置矩阵方便使用

z = -1:0.1:31;
if k==10        	% 下面的y1是不同时候的k时的类似于函数表达式的式子
    y1 = A(1)+A(2).*z+A(3).*z.^2+A(4).*z.^3+A(5).*z.^4+A(6).*z.^5+A(7).*z.^6+A(8).*z.^7+A(9).*z.^8+A(10).*z.^9+A(11).*z.^10;%最后表达式用于绘图
elseif k==5
    y1 = A(1)+A(2).*z+A(3).*z.^2+A(4).*z.^3+A(5).*z.^4+A(6).*z.^5;%最后表达式用于绘图
elseif k==4
    y1 = A(1)+A(2).*z+A(3).*z.^2+A(4).*z.^3+A(5).*z.^4;%最后表达式用于绘图
elseif k==3
    y1 = A(1)+A(2).*z+A(3).*z.^2+A(4).*z.^3;%最后表达式用于绘图
elseif k==2
    y1 = A(1)+A(2).*z+A(3).*z.^2;%最后表达式用于绘图
elseif k==1
    y1 = A(1)+A(2).*z;%最后表达式用于绘图
end

plot(z,y1);
hold on

结果就是 回归到底是做预测还是用来去脏数据？ 的那张图。

注意if k==10以及所有elseif语句段的意思：
按A所得的向量作为一元多次多项式的系数，来算在z的横坐标值上的纵坐标的值，最后plot(z,y1);画出图像。
这一步有一个简单的函数polyval来代替，后面用polyfit函数时会用到。

可能比较晦涩难懂，具体可以对比参考mathwork官网的polyval函数介绍，想一下还是很容易懂的。点这里

当k改为5时，结果

当k改为3时，结果

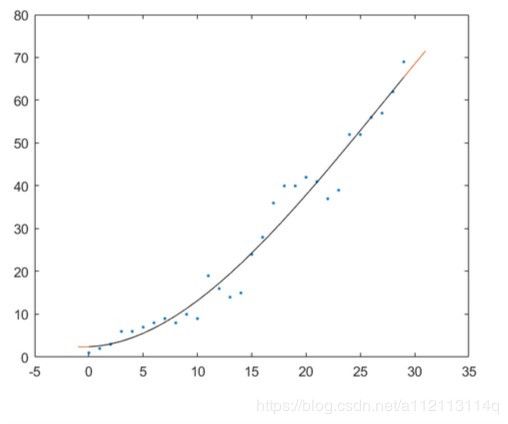
当k改为2时，结果

当k改为1时，结果

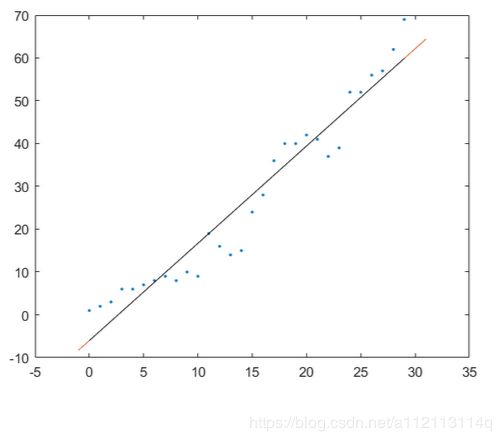
当k≠1时，我们可以看到这条线是曲线，对应曲线回归（非线性回归）
当k=1，直线，对应直线回归。

当我们查线性回归的matlab代码时会看到polyfit和regress函数，这两个函数内部执行的代码和我们前面看到的是差不多的。就是说这两个函数的思路就是最小二乘法。

4.函数polyfit（线性）

先看一个例子

y=[143 145 146  147 149  150  153  154  155 156  157  158 159  160  162 164];
x=[88 85  88   91  92   93  93   95   96  98  97  96  98   99   100 102];

plot(x,y,'.');
a=polyfit(x,y,1) 	% 函数polyfit求拟合曲线,1是最高次数，即x^1
hold on ;
temp=polyval(a,x) 	% 函数polyval计算以a为系数组成的多项式在x=[x向量]中每一个值的值。如例1，    
                        % 这里f(x) = 1.2903x+31.7713 

% 例1.
% 计算多项式 f(x)=3x^2+2x+1在点 x=5,7,9 处的值。多项式系数可以由向量 [3 2 1] 表示。
% p = [3 2 1];
% x = [5 7 9]; 分别计算f(x)在x=5、x=7、x=9的值，存储到y中
% y = polyval(p,x)

结果如下：

所以polyfit就相当于我们上面说的那个k=1的情况。
把下面这一段代码加到3-2代码块的最后，画出来的图效果一样。

A = fliplr(A); 		% 将A向量里面的值顺序颠倒
     		        % 因为我们下面用的函数polyval输入参数A需要从最高次项开始
      			% 而正规方程解是从零次开始
yy = polyval(A,x);
plot(x,yy,'k');
hold on；

5.函数regress（线性）

注：
我在写博客的时候把states和stats弄混了，有的可能没有看到就没有更正。

先看代码的完全版：

[b,bint,r,rint,stats]=regress(y,X,n)

X的形式比较特殊，等会会说

5-1.输出b,bint,r,rint,stats

• b
  类似我们的正规方程解θ，就上上面我们所求的A，是多项式系数向量。

• bint
  b的置信区间，这个要学好概率统计的才知道去了。对于小白来说，就是我们求得的b在这个区间内比较好。

• r
  残差，数据点的y值与拟合线的y值的差，就是类似于我们前面说的最小二乘法的那个$y_i-{\hat{y}}_i$

• rint
  r的置信区间，简单说和bint一样，r在这个区间内比较好。

• stats
  是个包含四个个值的向量。
  假如是0.9644 ， 244.0571 ， 0.0000 ， 3.12777

1. 第一个是相关系数的平方（$R^2$），在0.9-1之间表示X和y相关性比较好，越近1越好。
   注，原来写的是相关系数，没有平方，后来发现错误改的。有的地方可能没看到没改，统一一下是相关系数的平方

2. 第二个是应用F检验的F统计量的值，公式为
   $$F=\frac{S_x^2}{S_y^2}$$
   其中
   $$S_k^2=\frac{1}{n-1}\sum _{i=1}^n(k-\hat{k}{)}^2,k=x或y$$这个也要学好概率统计的比较熟悉，小白知道怎么用就行吧，我等会会说。

3. 第三个是F统计量的值对应的概率，我们记为p，小白要知道这个概率越小越好，会有一个小的标准，我们先记为$\alpha$，及： $p<\alpha$时，回归模型成立。

4. 第四个是残差的方差估计，不同资料称呼还不同。这个我还没有查到具体用法，请朋友赐教。但是就我已知的这个没有用到过。

5-2.应用

5.2-1.一元线性回归

数据我们跟上面用一样的

y=[143 145 146  147 149  150  153  154  155 156  157  158 159  160  162 164];
x=[88 85  88   91  92   93  93   95   96  98  97  96  98   99   100 102];
plot(x,y,'.');
hold on ;

X = [ones(16,1),x'];		%X的特殊形式
[b,bint,r,rint,stats]=regress(y',X,0.05);
b,bint,r,rint,stats		% 输出四个输出，等会作分析
b = b';				% b是列向量，等会用polyfit要横向量，所以转置处理。
b = fliplr(b);			% 上面也说过，regress求得的与正规方程解也相反，所以要倒序处理
yy = polyval(b,x)；
plot(x,yy)

结果截图如下：

代码块里面的b = b’;b = fliplr(b); 这两个我是根据b的输出结果发现b是列向量并且与正规方程解相反才知道要这样做，后来补上来的。不然会有各种错误警告之类的。

b可以对比polyfit代码块里面的a就知道为什么要这么做了

• 然后分析bint，b的第一个值在12.3196与51.229，对。第二个值在1.0846与1.4960之间，也对。
• 分析r，残差$y_i-{\hat{y}}_i$发现第二个是3.5523有点大，其他都好像还行。这个还可以用我第一篇的异常值判别来做具体分析。
• 分析rint，好像都在区间里面，我没具体看了。
• 分析stats，第一个相关系数0.9282，在0.9-1之间很好。第二个F统计量的值180多，暂时不用。第三个F统计量的值对应的概率0.0000，其实不是0只不过小数点后面太多，没有显示出来。然后这么小可以肯定的是肯定小于$\alpha$的。$\alpha$有概率统计书的同学可以查书后面的分布表，matlab上面怎么查我还不知道。有的资料好像默认$\alpha =0.001$我不确定对不对，后来又发现默认是0.05。 第四个残差的方差估计3.1277，未知用途，暂时作不用处理。

5.2-1.多元线性回归

上面所说的，polyfit、regress，都是回归的一元多次（一次二次甚至更多）多项式。
下面的regress将可以回归多元多次多项式。（主要不同在多元）
参考文章这里与这里

下面是完整的代码，供复制用，有基础的的可以直接看，小白还是跟着我一步一步来吧。
因为代码与结果截图比较长，所以我之后分段作分析。

%导入数据，并画出第一个三维图
x1=[3.5 5.3 5.1 5.8 4.2 6.0 6.8 5.5 3.1 7.2 4.5 4.9 8.0 6.5 6.5 3.7 6.2 7.0 4.0 4.5 5.9 5.6 4.8 3.9];
x2=[9 20 18 33 31 13 25 30 5 47 25 11 23 35 39 21 7 40 35 23 33 27 34 15];
x3=[6.1 6.4 7.4 6.7 7.5 5.9 6.0 4.0 5.8 8.3 5.0 6.4 7.6 7.0 5.0 4.0 5.5 7.0 6.0 3.5 4.9 4.3 8.0 5.0]; % x3暂时留着备用
Y=[33.2 40.3 38.7 46.8 41.4 37.5 39.0 40.7 30.1 52.9 38.2 31.8 43.3 44.1 42.5 33.6 34.2 48.0 38.0 35.9 40.4 36.8 45.2 35.1];

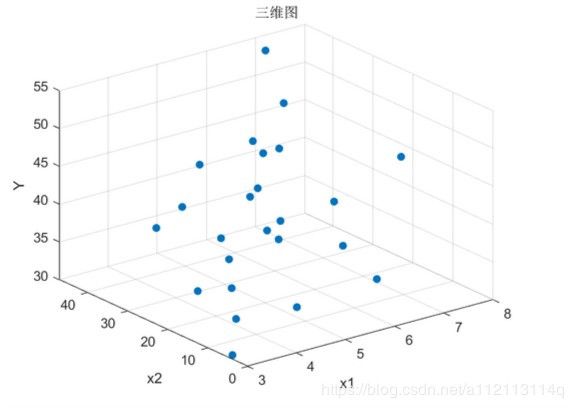
scatter3(x1,x2,Y,'filled');hold off;    % scatter可用于画散点图
xlabel('x1');      			% x坐标命名
ylabel('x2');				% y坐标命名 
zlabel('Y');				% z坐标命名
title('三维图');				% 图标题

%regress函数作回归
X=[ones(24,1),x1',x2'];   	     	          % X的特殊形式，等会作不同多项式回归的时候改这里就行，我会举例出来的。
[b,bint,r,rint,stats]=regress(Y',X,0.05);	  % 比如作二元二次多项式回归
b,bint,r,rint,stats

%将regress的结果画出来
scatter3(x1,x2,Y,'filled');hold on;   		  % 重新画一个三维图
x1fit = min(x1)-5:1.5:max(x1)+5;  		  % 设置x1的数据间隔，为画平面（网格组成）作铺垫。
x2fit = min(x2)-5:3:max(x2)+5;     		  % 设置x2的数据间隔
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit)             % 生成一个二维网格平面，也可以说生成X1FIT,X2FIT的坐标
YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT     	  % 这一步很重要，这个YFIT的形式要和X矩阵的形式一样。
mesh(X1FIT,X2FIT,YFIT)        			  % X1FIT，X2FIT是网格坐标矩阵，YFIT是网格点上的高度矩阵
xlabel('x1');
ylabel('x2');
zlabel('Y');
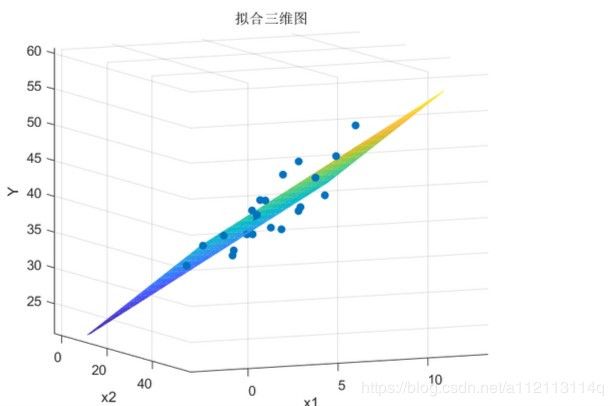
title('拟合三维图')

分析如下：

%导入数据，并画出第一个三维图
x1=[3.5 5.3 5.1 5.8 4.2 6.0 6.8 5.5 3.1 7.2 4.5 4.9 8.0 6.5 6.5 3.7 6.2 7.0 4.0 4.5 5.9 5.6 4.8 3.9];
x2=[9 20 18 33 31 13 25 30 5 47 25 11 23 35 39 21 7 40 35 23 33 27 34 15];
x3=[6.1 6.4 7.4 6.7 7.5 5.9 6.0 4.0 5.8 8.3 5.0 6.4 7.6 7.0 5.0 4.0 5.5 7.0 6.0 3.5 4.9 4.3 8.0 5.0];	% x3暂时留着备用
Y=[33.2 40.3 38.7 46.8 41.4 37.5 39.0 40.7 30.1 52.9 38.2 31.8 43.3 44.1 42.5 33.6 34.2 48.0 38.0 35.9 40.4 36.8 45.2 35.1];

scatter3(x1,x2,Y,'filled');hold off;    % scatter可用于画散点图
xlabel('x1');         			% x坐标命名
ylabel('x2');			        % y坐标命名 
zlabel('Y');   			        % z坐标命名
title('三维图');  		        % 图标题

结果截图：

在这个图里面是可以旋转看数据点的三维分布的。并且可以平移、放大缩小等。

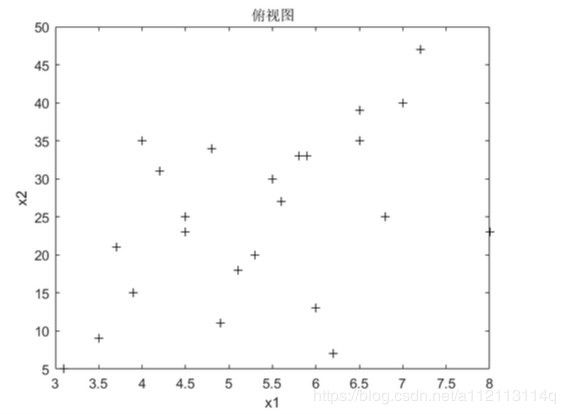
%画出侧视图和俯视图
plot(x1,Y,'r+');hold on;	% x1与Y的平面图（侧视图）
plot(x2,Y,'+');hold off;	% 同上，x2与Y的，因为hold on 所以画在一张图上
legend('x1','x2');		% 表示区分x1和x2
title('侧视图')

plot(x1,x2,'k+');hold off;	%另外画一个俯视图。
xlabel('x1');
ylabel('x2');
title('俯视图')

结果截图：

可以结合三维图，侧视图和俯视图想象一下在空间上数据点时怎么分布的，等会作二元一次多项式回归（平面回归）。

%regress函数作回归
X=[ones(24,1),x1',x2']; 			% X的特殊形式，等会作不同多项式回归的时候改这里就行，我会举例出来的。
[b,bint,r,rint,stats]=regress(Y',X,0.05);	% 比如作二元二次多项式回归
b,bint,r,rint,stats

结果：

可以看到残差有到3的，并且stats的第一个数值相关系数为0.82，相关性不是很好。所以说二元一次不太好，下面会把代码补完知道平面也画出来。然后用二元二次来回归。

%将regress的结果画出来
scatter3(x1,x2,Y,'filled');hold on;   	   % 重新画一个三维图
x1fit = min(x1)-5:1.5:max(x1)+5;	   % 设置x1的数据间隔，为画平面（网格组成）作铺垫。
x2fit = min(x2)-5:3:max(x2)+5;   	   % 设置x2的数据间隔
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit)      % 生成一个二维网格平面，也可以说生成X1FIT,X2FIT的坐标
YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT 	   % 这一步很重要，这个YFIT的形式要和X矩阵的形式一样。
mesh(X1FIT,X2FIT,YFIT)    		   % X1FIT，X2FIT是网格坐标矩阵，YFIT是网格点上的高度矩阵
xlabel('x1');
ylabel('x2');
zlabel('Y');
title('拟合三维图')

结果：

这里的YFIT一定要是矩阵，才能用mesh函数，不然会报错。具体可查mathwork官网，mesh函数的介绍。点这里
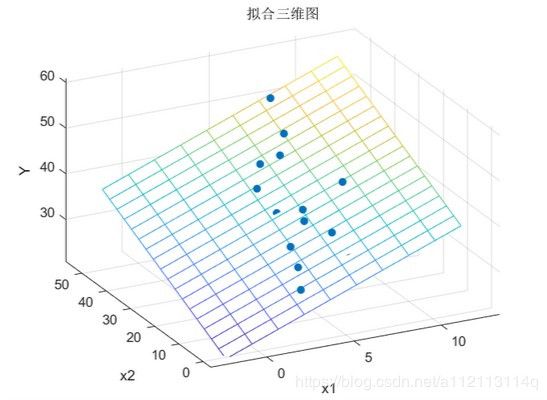
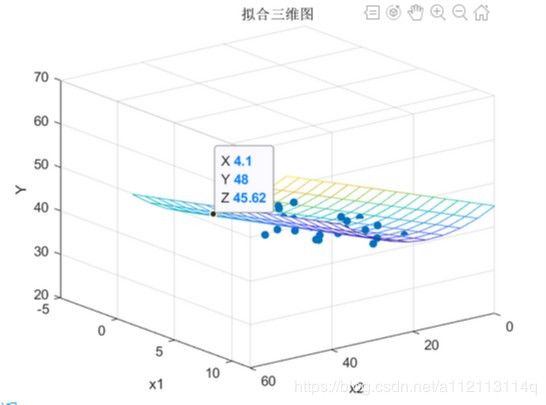
拟合的平面图，我旋转不同角度，截图了两张。

图1. ↓

图2.↓

从图1可以看到12个完整的点，1个半圆点。半圆说明数据点落在平面上，也就是回归出来的多项式，拟合出来的平面经过了这个点。
从我们第一个三维图可以知道不止这么些点，因为在平面下面去了，具体看图2，大致有8个左右的点在平面下面。

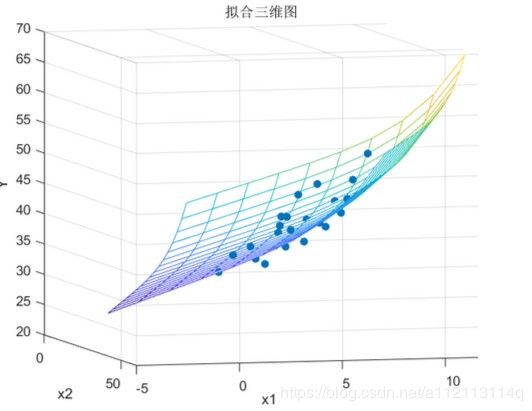
下面我们试一下二元二次多项式回归。
把

X=[ones(24,1),x1',x2'];                    % X的特殊形式

改成

X=[ones(24,1),x1'.^2,x2']; 		% X的特殊形式

再把

YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT     % 这一步很重要，这个YFIT的形式要和X矩阵的形式一样。

改成

YFIT = b(1) + b(2)*X1FIT.^2 + b(3)*X2FIT  % 这一步很重要，这个YFIT的形式要和X矩阵的形式一样。

结果就变成了这样的曲面：

继续进行改动，因为我看了相关系数是0.8275，不太好（不截图了）
再改

X=[ones(24,1),x1'.^5,x2'.^5,x1',x2',x1'.*x2']; 
% 与（这个不要复制）
YFIT = b(1) + b(2)*X1FIT.^5 + b(3)*X2FIT.^5 + b(4)*X1FIT + b(5)*X2FIT + b(6)*X1FIT.*X2FIT

结果截图：

相关系数为0.8428，相比之下会更好，可以继续进行改动。直至相关系数令人满意为止。

到这里regress算是介绍完了。

6.函数nlinfit（非线性）

6-1.引入

最开始介绍线性回归，说是拟合的一条线。其实也不竟然。regress回归出来的多元多次多项式（曲面）我们也叫他为线性回归，只不过是多元线性回归和一元线性回归的区别罢了。nlinfit函数才是我们非线性回归的真正要用的。
参考文章：这里与这里

现在我有这样的数据

x=[ 0,47,93,140,186,279,372,465,558,651];
y=[18.98,27.35,34.86,38.52,38.44,37.73,38.43,43.87,42.77,46.22];

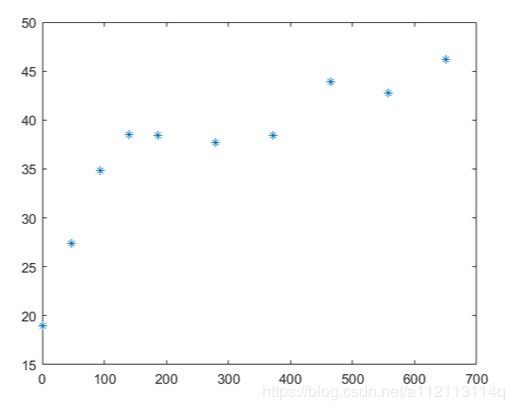
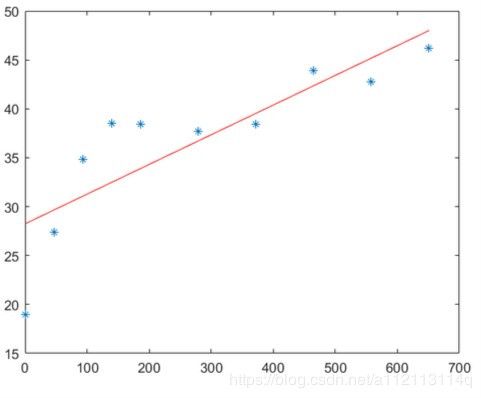
用了线性回归的一元一次，二次，三次分别回归得相关系数分别是0.7左右0.8左右0.9左右，如下面三张图。代码不发了，看懂前面这里应该自己会做。

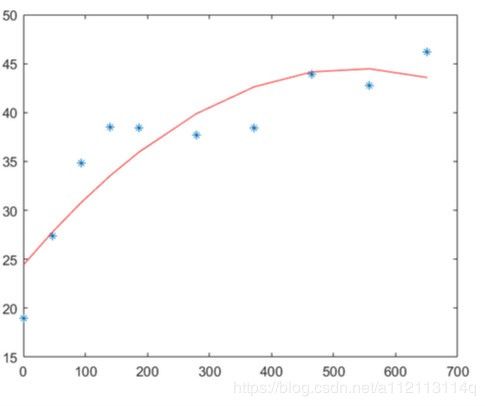
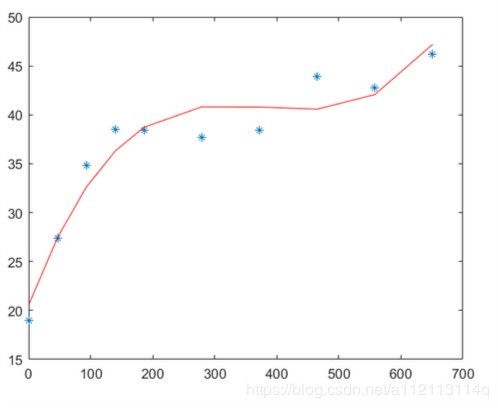
为什么你的是折现？
我没有取足够多得数据点来画。

为什么线性相关系数很好了还要用非线性？总用线性不好得时候，假如我用 $y=e^x$画数据点要你回归，那肯定我们应该得$y=e^x$这个函数啊。

而一开始我们是不晓得就是$y=e^x$这个函数的，所以我们会用$y=a{e}^x$，a是参数，这样带参数的函数逐步的回归。类似于最小二乘法。最后让matlab帮我们确定参数a的值。

$y=a{e}^x$，这个就叫数学模型。所以非线性回归就需求我们学习记忆很多很多的模型。然后看到数据比较像哪个模型，或哪几个模型。最后确定好模型再确定好参数。怎么确定模型等会也会说。

那要是出现了新的没有过的模型怎么办？这个就相当于建模了。学数学的朋友们的事去了。

扯了这么多，下面正式进入话题。

6-2.应用

还是上面那个数据，看图片非线性的模型有点像这个$y=\sqrt{x}$ ，或者是这个 $y=ln(x)$或者是其他的。

现在我随便用个这样的模型$y=a+b{x}^c$，我也不知道它的名字，随便起个名字叫fun

x=[ 0,47,93,140,186,279,372,465,558,651];
y=[18.98,27.35,34.86,38.52,38.44,37.73,38.43,43.87,42.77,46.22];

plot(x,y,'*');hold on;
fun=inline('a(1)+a(2)*x.^a(3)','a','x');		%类似于我们之前用到过的X的特殊形式，
							% 这里的inline叫内联函数，相当于一个自定义函数的功能
							% 后面我会说。
b0 = [18,0.9,0.5]; 					% 设定初始参数，怎么求后面说
xx = linspace(min(x),max(x),100);			% 画初始参数的拟合曲线
yy = b0(1)+b0(2)*xx.^b0(3);
plot(xx,yy,'-or');hold off;

[b,r,j]=nlinfit(x,y,fun,b0);
b,r,j

yy = b(1)+b(2)*xx.^b(3);				% 画非线性回归的拟合曲线
plot(x,y,'*');hold on;
plot(xx,yy,'-r');hold off;

按照上面代码中第一次见到的代码顺序，先讲inline内联函数
这里把我的初始参数的拟合曲线图发上来

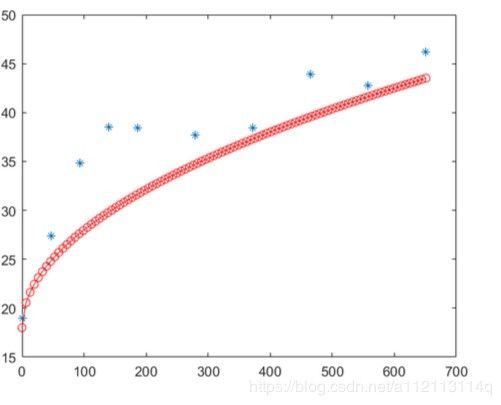
6-2-1.内联函数inline

还记得上面regress的X矩阵的特殊形式吗？像这样

X=[ones(24,1),x1',x2'];

还有于X形式相对应的这个

YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT；

在线性回归中，我们要确定一个我们想要的函数来回归拟合数据。非线性回归是一样的，只是这里我们多用了一个内联函数inline来表达我们想要的函数。

那线性回归可不可以用这个内联函数呢？应该是可以的，只是我还没有研究而已。另外注意一下，mathwork官网提示，自哪年哪个版本起（不记得了），不再用内联函数而用匿名函数去了。

fun=inline('a(1)+a(2)*x.^a(3)','a','x'); 

每个输入参数都有一对单引号，并且第一个参数是方程的形式，第二个参数是参数（数学上的参数），第三个参数是未知变量。

下面求的yy也和YFIT的功能一样。

6-2-2.初始参数的设定方法

1. 函数特征分析
2. 输入几组值求解方程

就我这个例子来说，我用的是函数特征分析，也就是分析一些高中学过的，所以我的初始参数已经差不多很接近最后的拟合结果b了
b0 = [18,0.9,0.5]; $y=a+b{x}^c$

• 18对应a，我们可以从x和y的数据规律看出来，当x为0时，y是18点几，由我们这个函数模型的特殊性，a就很容易确定为18了嘛，点几不用很清楚，这是matlab拟合的事。
• 0.9对应b，高中见过$x^{0.5}$也就是$\sqrt{x}$吧，可以想一下这个图像，已经差不多和那个数据点的趋势差不多了。本来我还是参数1的。
• 0.5对应c，就是用$\sqrt{x}$来做初始的参数。

另外有时候可以看数据点的一些最值平均值众数什么的，比如y最大值是523，数据点是（62，523），咱们就由$18+b{x}^{0.5}$推一下b是多少。等之类的方法

第二个方法：solve函数求解方程
matlab代码
这个solve函数我有两个问题一直还没有解决，请朋友们赐教
solve函数求不出来值，不知道是不是方程太复杂的原因。
solve函数求出来的值，作为初始值给nlinfit分析会出现一些溢出等问题
下面是问题（英文）和百度渣翻

some columns of the Jacobian are effectively zero at the solution,indicating that the model is insensitive to some of its parameters.that may be because those parameters are not present in the model,or otherwise so nor affect rhe predict values. it may also be due to numerical underflow in the model function ,witch can sometimes be avoided by choosing better initial parameter values, or by rescaling or recentering . parameter estimates may be unreliable.

雅可比矩阵的某些列在解的时候实际上为零，这表明模型对其某些参数不敏感。这可能是因为这些参数不在模型中，或者在其他方面不影响预测值。这也可能是由于模型函数中的数值下溢，有时可以通过选择更好的初始参数值，或通过重新缩放或重新居中来避免。参数估计可能不可靠。

fun=inline('a(1)+a(2)*x.^a(3)','a','x'); %solve函数也要用到这个形式

我先把sovle函数的两个问题的代码发出来，简单解释一下给小白，就不具体分析了。
能求出来值，作为初始值给nlinfit分析会出现一些溢出等问题的代码

syms b1 b2 b3;		% syms后面接变量名，相当于c语言的变量声明。
					% 不这样会导致后面的solve函数出现未知变量问题
[b1,b2,b3] = solve(b1+b2*47.^b3 == 27.35,b1+b2*93.^b3 == 34.86,b1+b2*140.^b3 == 38.52,[b1,b2,b3])

结果截图

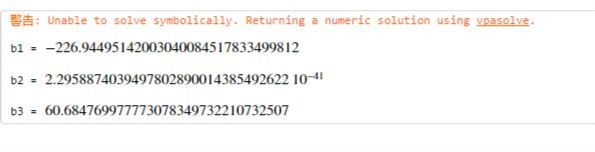
看那个-226这个值也实在是太小了，不知道是不是溢出问题。
求不出来值的代码

syms b1 b2 b3 x;
equation1 = b1+b2*47.^b3 == 27.35;
equation2 = b1+b2*93.^b3 == 34.86;
equation3 = b1+b2*140.^b3 == 38.52;
eqn = [equation1,equation2,equation3];
b0 = solve(eqn,[b1 b2 b3],'ReturnConditions',true);
b1

结果截图

solve的输入参数分别是方程（可单个可多个），变量。思想就是把我们本来要求的参数（数学上的那个参数）作变量，输入几组数据，求出这个变量来。

6-2-3.输出b、r、j

我上面那段代码的结果（输出部分）

• b是我们的要的方程（比如我的例子就是这个$y=a+b{x}^c$）的系数向量。
  所以就是 ， matlab非线性回归最后拟合出来的
  a=18.7887 ， b=3.7036 ， c=0.3032
• r是残差，与5-1的r一样，具体请看那。
• J是雅可比矩阵，具体什么用我也还没搞清楚。

那我们用什么参数来判断这个非线性回归拟合得好不好呢？线性回归我们有相关系数，和f统计量得值对应的概率。这里根据知乎的这篇问答来看，用相关系数的平方$R^2$应该是可以用来判断的，并且判断规则和上面regress一致。

所以我们这里我们怎么求呢？

R = cov(x,y)/(cov(x).^0.5*cov(y).^0.5)	% 这里是根据相关系数的定义求的。
%或
R = corrcoef(x,y)			% matlab 提供的方便求相关系数的

%最后别忘了平方
R2 = R.^2

cov函数什么意思，我上一篇的4-2的代码块里面有解释。

结果截图

注意是副对角线上的两个同样的值。主对角线上我暂时不知道是什么。
$R^2=0.7035$，可见拟合得不是很好。但是对于非线性回归来说，这也不容易了。