此文讨论一个无向图中存在环的问题,在不管多复杂的连通图中寻找出所有的环,使用删除点的方法。
此外,这个版本的查找方法可以用于其他场景:找出无向图中所有的环的算法
结果能找到最小的环,或许要靠运气,输出该输出的环...............,这是原始算法。
改进:
可以输出最大环(通过跳过多度点),可以输出最小子环(通过使用最短路径)......................
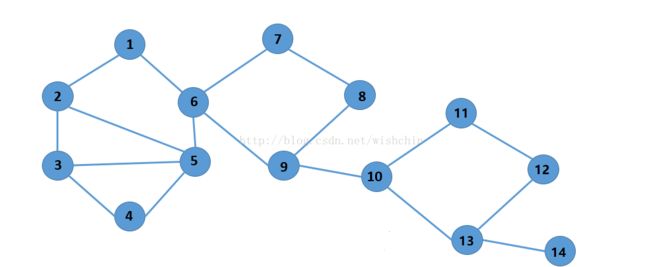
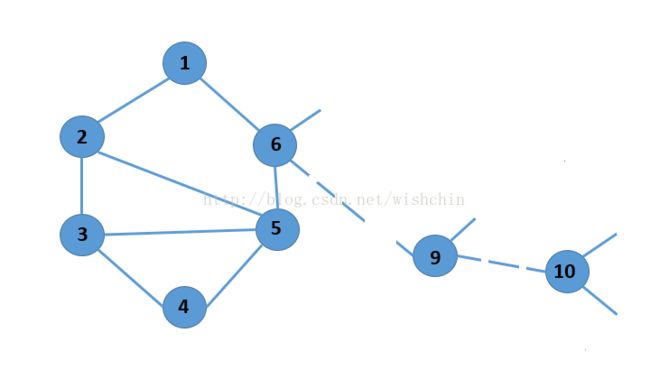
使用一个图:
比如在上图中,存在多个环(1,2,3,4,5,6)(6,7,8,9)(1,2,5,6)(1,2,3,5,6).........
怎么寻找呢?
一、使用删除边法
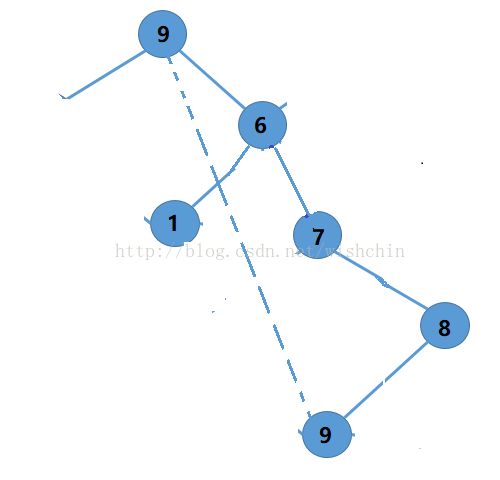
本例中,从顶点9开始,构建DFS
1.首先删除所有度数为1的点,这样点14就被删除。这样只剩下多度顶点的环
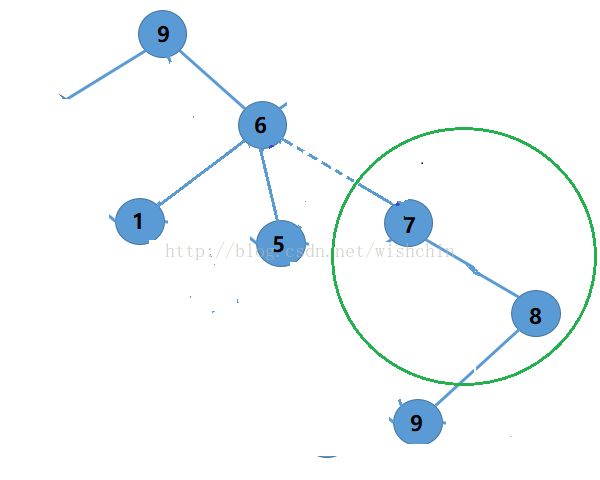
2. 若从顶点9开始,找到了环(9,8,6,7),对于顶点8和顶点7,其所有链接的边都在当前环上,则可以删除掉两个顶点;
而9除了处于环中的边,还有其他边,则不能删除。此外,顶点6也不能删除。
判断条件: 若顶点X链接的边在这一个环上,则可以删除此顶点。
例如:在图中,删除的点为7和8,同时所有的链接边也删除。输出环(9.8.7.6)。
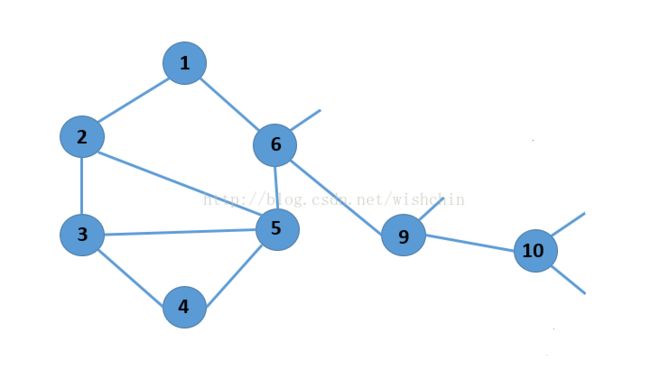
3. 使用堆栈,再次查找10,可以输出环(10,11,12,13),同时可以删除顶点(11,12,13)。此时顶点10 的度置位1,标识为已遍历状态。
4.每次查找环,都删除度为1的节点和连接边。此时可以删除10,9,树退化为一颗子树。
5.到了一个查找重复环的时候
5.1. 此时没有单度节点,
5.2. 出现问题,得重新考虑了!!!
从顶点6开始找到所有的环:注意此过程依然为生成树的过程,每一个边都被设定为有向边。
Code :
// 寻找联通集合的闭包,判断是否连通,返回闭包
public static void findSub(Boolean adjM[][], Set votex, ArrayList> loopSets) {
if (votex.size() < 2) {// 治标不治本
return;
}
for (int m = 0; m < adjM.length;++m){
adjM[m][m] =false;
}
// 计算顶点的度
Integer[] degrees = new Integer[adjM.length];
degrees = calVotexDegree(adjM);
//循环查找,找到所有的度不为1的闭包
boolean isdeleted = true;
while( isdeleted ){
isdeleted = false;
degrees = calVotexDegree(adjM);
delete1Degree(adjM, degrees);// 删除度数为1 的边
int l1 = votex.size();
// 更新联通集合
for (int i = 0; i < degrees.length; ++i) {
if (degrees[i] == 0) {
votex.remove(i);
for (int m = 0; m < adjM.length;++m){
adjM[i][m] = false;//更新度,若被移除则相关的邻接都置为false
adjM[m][i] = false;
}
}
}
int l2 = votex.size();
if(l1!=l2) isdeleted = true;
}
// 遍历所有节点,逐个取出,去除非环节点
Set loop = new HashSet();
Set sub = new HashSet();
boolean isBlankX = false;
boolean isFind = false;
for (int ob : votex) {
int obj = ob;
sub.add(obj);
int idx = obj;
for (int j = idx; j < adjM[idx].length;) {
if (adjM[idx][j]) {
if (sub.contains(j) && idx != j) {
transSet(sub, loop);// 若已存在元素,则存在环,复制出环
loopSets.add(loop);
votex.removeAll(loop);
sub.clear();
findSub(adjM, votex, loopSets);
isFind = true;
if (votex.size() < 3) {// 剩余两个就不再寻找
isBlankX = true;
}
++j;
} else {
sub.add(j);
++j;
}
} else
++j;
}
if (isFind)
break;
}
return;
} // 输出顶点的度
public static Integer[] calVotexDegree(Boolean adjM[][]) {
Integer[] degrees = new Integer[adjM.length];
for (int i = 0; i < adjM.length; ++i) {
degrees[i] = 0;
for (int j = 0; j < adjM[i].length; ++j) {
if (adjM[i][j] == true) {
degrees[i] = degrees[i] + 1;
}
}
}
return degrees;
}// 更新矩阵:删除权值为1和0的边
public static void delete1Degree(Boolean[][] adjM, Integer[] degrees) {
for (int j = 0; j < adjM.length; ++j) {
adjM[j][j] = false;// 自身边消除掉
if (degrees[j] < 2) {
for (int k = 0; k < adjM[j].length; ++k) {
adjM[j][k] = false;
adjM[k][j] = false;
}
degrees[j] = 0;
}
}
}输出结果:输出结果具有一定的概率性,和顶点的排序有关。