Xgboost系统设计：分块并行、缓存优化和Blocks for Out-of-core Computation

Xgboost的原理我之前已经介绍过了，详见《（二）提升树模型：Xgboost原理与实践》。 最近，想起来阅读Xgboost源论文中还没有读过的一块，即第4章SYSTEM DESIGN系统实现。第4章包括3个小节：

• Column Block for Parallel Learning

• Cache-aware Access

• Blocks for Out-of-core Computation

在阅读源论文的基础上，本篇博客依次介绍这3个部分。

一、分块并行 – Column Block for Parallel Learning

在建树的过程中，最耗时是找最优的切分点，而这个过程中，最耗时的部分是将数据排序。为了减少排序的时间，Xgboost采用Block结构存储数据。它有如下几点特征：

• Block中的数据以稀疏格式CSC进行存储。CSC格式请参考该文章。

• Block中的特征进行排序（不对缺失值排序），且只需要排序一次，以后分裂树的过程可以复用。

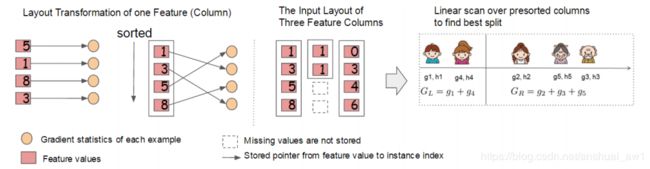
对于exact greedy算法来说，Xgboost将所有的数据放到了一个Block中。在Block中，可以同时对所有叶子进行分裂点的计算，因此对Block进行一次扫描将可以得到所有叶子的分割特征点候选者的统计数据。（We do the split finding of all leaves collectively, so one scan over the block will collect the statistics of the split candidates in all leaf branches.） Block 中特征还需存储指向样本的索引，这样才能根据特征的值来取梯度。如下图所示：

对于approximate算法来说，Xgboost使用了多个Block，存在多个机器上或者磁盘中。每个Block对应原来数据的子集。不同的Block可以在不同的机器上计算。该方法对Local策略尤其有效，因为Local策略每次分支都重新生成候选切分点。

Block结构还有其它好处，数据按列存储，可以同时访问所有的列，很容易实现并行的寻找分裂点算法。缺点是空间消耗大了一倍。

从时间复杂度上来分析：

对于exact greedy算法：复杂度从原来的$O(Kd||x|{|}_0\log n)$降为$O(Kd||x|{|}_0+||x|{|}_0\log n)$，其中$d$为树的最大深度，$K$为树的数量，$||x|{|}_0$为训练集中非缺失值的个数。这样，Exact greedy算法就省去了每一步中的排序开销。当$\log n$大的时候，省去的时间就很多了。

对于approximate算法：复杂度从原来的$O(Kd||x|{|}_0\log q)$降为$O(Kd||x|{|}_0+||x|{|}_0\log B)$，其中$q$是候选分裂点的数量，$B$为每个Block中最大的行数。$q$一般取值在32到100之间，因此省去的$\log q$也是值得的。

这里，我分析一下时间复杂度，来自参考文献【4】:

如果我们不使用block结构时，即采用原始的稀疏精确算法时。为了在每一个节点node找到最优的分割，我们需要对每一个特征进行排序。则每层layer的时间复杂度非常粗略地近似$O(\Vert \mathbf{x}{\Vert }_0\log n)$: 这是因为，如果对于特征$1\le i\le m$，每个特征$i$有$\Vert \mathbf{x}{\Vert }_{0i}$非零值，然后，在每一层我们需要排序，且每个特征最多有$n$个（即样本为$n$），因为所有特征的长度为${\sum }_{i=1}^m\Vert \mathbf{x}{\Vert }_{0i}=\Vert \mathbf{x}{\Vert }_0$，在这种情况下，排序时间不超过$O(\Vert \mathbf{x}{\Vert }_0\log n)$(注：快排的时间复杂度为$n\log n$)。在此基础上，乘以$K$个树和$d$层，因此时间复杂度为$O(Kd\Vert \mathbf{x}{\Vert }_0\log n)$ 。

如果我们使用block结构时，在一开始我们就已经对特征进行了排序，不需要在每个节点都排序。正如作者强调的，这时候时间复杂度降到了$O(Kd\Vert \mathbf{x}{\Vert }_0)$，这是因为，我们对block扫描一遍时就可以得到各个节点的最优切分。再加上一开始排序的复杂度为$O(\Vert \mathbf{x}{\Vert }_0\log B)$，(按照意义，这里$B$就是$n$)。因此，总时间复杂度为$O(Kd||x|{|}_0+||x|{|}_0\log B)$。

二、缓存优化 – Cache-aware Access

使用Block结构的一个缺点是取梯度的时候，是通过索引来获取的，而这些梯度的获取顺序是按照特征的大小顺序的。这将导致非连续的内存访问，可能使得CPU cache缓存命中率低，从而影响算法效率。如下图所示：

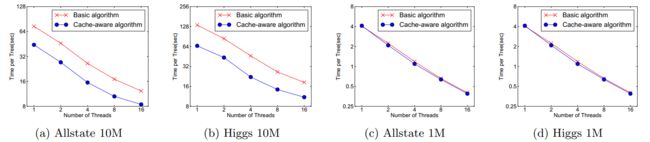
因此，对于exact greedy算法中, 使用缓存预取（cache-aware prefetching）。具体来说，对每个线程分配一个连续的buffer，读取梯度信息并存入Buffer中（这样就实现了非连续到连续的转化），然后再统计梯度信息。该方式在训练样本数大的时候特别有用，见下图：

可以看到，对于大规模数据，效果十分明显。

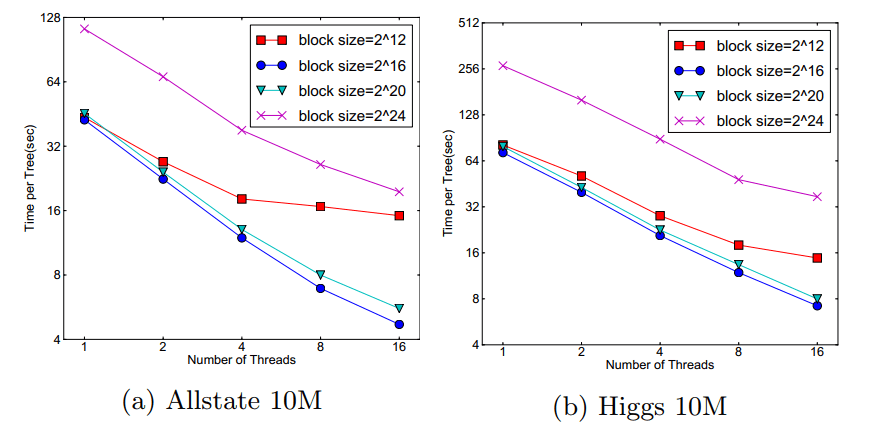
在approximate 算法中，对Block的大小进行了合理的设置。定义Block的大小为Block中最多的样本数。设置合适的大小是很重要的，设置过大则容易导致命中率低，过小则容易导致并行化效率不高。经过实验，发现2^16比较好。如下图：

三、Blocks for Out-of-core Computation

当数据量太大不能全部放入主内存的时候，为了使得out-of-core计算称为可能，将数据划分为多个Block并存放在磁盘上。计算的时候，使用独立的线程预先将Block放入主内存，因此可以在计算的同时读取磁盘。但是由于磁盘IO速度太慢，通常更不上计算的速度。因此，需要提升磁盘IO的销量。Xgboost采用了2个策略：

• Block压缩（Block Compression）：将Block按列压缩（LZ4压缩算法？），读取的时候用另外的线程解压。对于行索引，只保存第一个索引值，然后只保存该数据与第一个索引值之差(offset)，一共用16个bits来保存
  offset，因此，一个block一般有2的16次方个样本。

• Block拆分（Block Sharding）：将数据划分到不同磁盘上，为每个磁盘分配一个预取（pre-fetcher）线程，并将数据提取到内存缓冲区中。然后，训练线程交替地从每个缓冲区读取数据。这有助于在多个磁盘可用时增加磁盘读取的吞吐量。

参考文献

【1】XGBoost: A Scalable Tree Boosting System

【2】『我爱机器学习』集成学习（三）XGBoost

【3】GBDT算法原理与系统设计简介

【4】XGBoost paper - time complexity analysis