栈和逆波兰表达式
中缀表达式
1+2,1+3*2,1+(3*2*(1+3)),这些就是中缀表达式,就是我们 平时经常见到的形式,先算加减再算乘除,有括号的先算括号里面的,没有括号按照优先级顺序进行计算。但是,计算机处理中缀表达式却并不方便,因为没有一种简单的数据结构可以方便从一个表达式中间抽出,一部分算完结果,再放进去,然后继续后面的计算(链表也许可以,但是,代价也是不菲)。
若用链表进行计算,不断地更新值,更新节点,时间复杂度很高,代码量也不低.
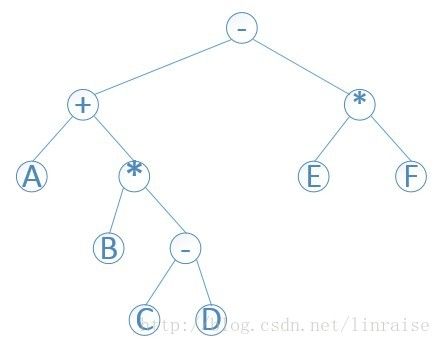
以A+B*(C-D)-E*F为例:
叫做中缀表达式原因就是它是由相应的语法树的中序遍历的结果得到的。
![]()
比如上图二叉树遍历结果
前序遍历:ABCDEFGHK(根节点排在最先,然后同级先左后右)
中序遍历:BDCAEHGKF(左节点排在最先,然后根节点,最后右)
后序遍历:DCBHKGFEA(左节点排在最先,然后右节点,最后根节点)
中序遍历如下图,中序比较重要
![]()
前缀表达式
前缀表达式就是波兰式,有相应的语法树前序遍历得到,
上图的前缀表达式为- + A * B -C D * E F
两种思路算出结果:
1.第一步是从左至右扫描表达式,如果一个操作符后面有两个操作数时,则先计算,用计算后的值替换(这个操作符和两个数)。重复此步骤,直至全部处理完,如- + A * B -C D * E F,先计算C-D,用计算后的值C'代替,- + A * BC' * E F。用B'代替B*C',-+AB'*EF,用A'代替A+B',-A'*EF,用E’代替E*F,然后为-A'E',最终的结果为A'-E'。
2,由以上分析思索如何去实现过程,首先我们可以逆序,采用栈的思想,多遍扫描表达式,需要将3个字符替换为1个字符,我们每次扫描到操作数时,则入栈,扫描到操作符,则弹出来两个数进行计算,计算后的值则压进栈中,按照顺序和思路则为出2入1,那么扫描结束后栈顶就是表达式结果。
3,那么我们需要几个栈呢?两个一个用来保存数字逆序,另一个用来保存操作符,因为操作符默认是从左到右的,所以就需要一个栈,前缀表达式往往需要用两个栈来计算,其中一个栈用来预处理:将字符串倒序压进栈中。
啊,我忘了保存,电脑睡眠,但是回来系统自己更新了,写了一上午的博客都没有保存,心痛,重来重来。
后缀表达式
后缀表达式就是逆波兰式,它是由相应的语法树后序遍历得到结果例如上面举的例子它的后缀表达式为 A B C D - * + E F * -
后缀表达式和前缀表达式看起来就像一对逆过程,实际上并不是这样子,还是有一定区别的。
中缀表达式转后缀表达式
如果熟练的话,可以根据给出的中缀表达式中序遍历画出相应的二叉树,然后后序遍历则为相应的后缀表达式。
例如:12 * (3 + 4) - 6 + 8 / 2
依次获取:
12 ,是数字,直接输出
后缀表达式:12
符号栈:
’ * ’ ,是运算符,入栈
后缀表达式:12
符号栈:*
’ ( ‘,左括号,直接入栈
后缀表达式:12
符号栈: * (
3 , 数字 ,输出
后缀表达式:12 3
符号栈: * (
‘ + ’,运算符 ,入栈
后缀表达式:12 3
符号栈: * ( +
4 ,数字,输出
后缀表达式:12 3 4
符号栈: * ( +
‘ )’,右括号,栈中元素依次出栈并输出知道遇到左括号,并且左括号也要出栈且不输出
后缀表达式:12 3 4 +
符号栈: *
‘ - ’,操作符,减号的优先级低于乘号所以乘号出栈并输出,此时站内没有符号,减号入栈
后缀表达式:12 3 4 + *
符号栈: -
6 ,数字,输出
后缀表达式:12 3 4 + * 6
符号栈: -
’ + ‘,操作符 ,优先级与减号相同(也就是说没有减号的优先级高)所以减号出栈输出,加号入栈
后缀表达式:12 3 4 + * 6 -
符号栈: +
8 ,数字 ,输出
后缀表达式:12 3 4 + * 6 - 8
符号栈: +
‘ / ’,操作符,比减号的优先级高直接入栈
后缀表达式:12 3 4 + * 6 - 8
符号栈: + /
2 ,数字,输出
后缀表达式:12 3 4 + * 6 - 8 2
符号栈: + /
中缀表达式获取完后,将栈中剩余元素依次出栈输出
后缀表达式:12 3 4 + * 6 - 8 2 / +
符号栈:
以上就是中缀表达式转后缀表达式。这是一位大佬的博客的分析过程,我觉得很棒,以后再继续理解。
https://blog.csdn.net/Coder_Dacyuan/article/details/79941743这位大佬更厉害,我觉得分析很到位
个人认为中缀转后缀的主要难点在于运算符的处理以及括号的处理,这是特别容易出错的地方,这一块出错了,结果就很容易出错。
若遇到的是运算符:a、如果该运算符的优先级大于栈顶运算符的优先级时,将其压栈
b、如果该运算符的优先级低于栈顶元素,将栈顶元素输出,接着和新的栈顶运算 符比较,若大于,则将其压栈,若小于,继续将栈顶运算符弹出并输出......(一直递归下去,直至运算符大于栈顶云算符为止)。
中缀转前缀参考大佬的代码,感觉逻辑特别清晰,比自己的代码要优秀太多:
#include
#include
#include
#include
#include
#include 逆波兰表达式求值
思路:先把中缀表达式转换为后缀表达式,然后再计算后缀表达式求出相关值,注意需要两个栈,一个栈用来存放操作符,一个栈用来存放操作数。还需要一个队列存放后缀表达式。
#include
#include
#include
#include
#include
#include 一定要弄清楚思路和处理方法,可以自己参照思路写出代码,逆波兰主要就是栈的应和处理问题的思路,大同小异。
注:要输入合法的表达式,不然会出错。代码中没有写当输入非法表达式时的处理情况。
本篇博客参考大佬的居多。自己算是整理加copy,以备来日之需。