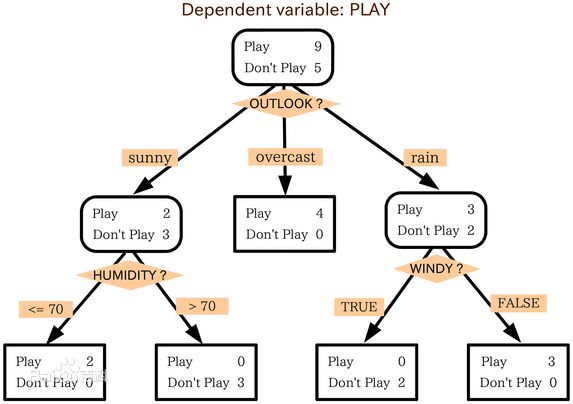
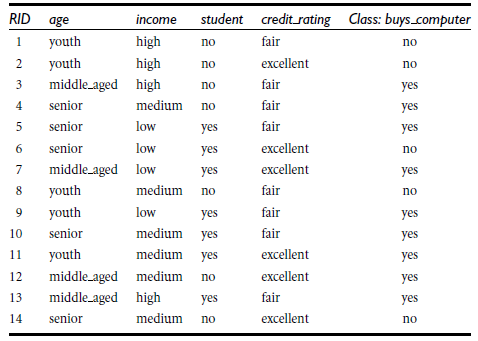
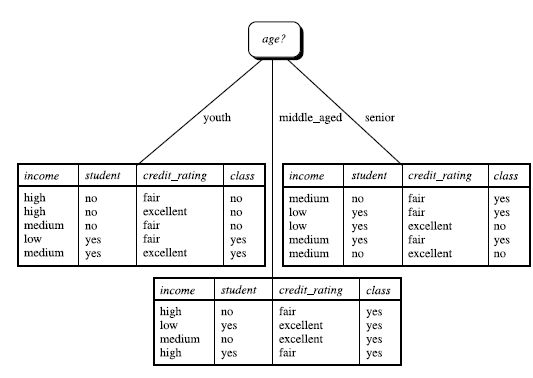
1.什么是决策树/判定树(decision tree)
决策树是一个类似于流程图的树结构,其中每个内部结点表示在一个属性上的测试,每个分支代表一个属性输出,而每个树叶结点代表类或者类分布。树的最顶层是根结点。
机器学习中分类方法中的一个重要算法
2.构造决策树的基本算法
树叶
2.1 熵(entropy)概念
信息和抽象该如何来度量?
1948年香农提出“信息熵(entropy)”的概念
一条信息的信息量大小和他的不确定性有直接的关系,要搞清楚一件非常非常不确定的事情,或者是我们一无所知的事情需要了解大量信息==》信息量的度量就等于不确定性的多少
例如:猜世界杯冠军,假如是一无所知,需要猜多少次?每个队夺冠的几率不是相等的
比特(bit)来衡量信息的多少
![]()
变量的不确定性越大,熵也就越大
2.2 决策树归纳算法(ID3)
1970-1980,J.Ross. Quinlan,ID3算法
选择属性判断结点
信息获取量(Information Gain):Gain(A) = Info(D)-Infor_A(D) (没有A时的信息熵-有A之后的信息熵)
通过A来作为节点分类获取了多少信息
没有按照年龄来分时的信息熵
按照年龄来分的信息熵
通过年龄分类的信息获取量
![]()
类似的,Gain(income)=0.029,Gain(student)=0.151,Gain(credit_rating)=0.048,所以选择age作为第一个根节点。
重复。。。
2.3 算法总结:
1) 树以代表训练样本的单个结点开始(步骤1)
2) 如果样本都在同一个类,则该结点成为树叶,并用该类标号(步骤2,3)
3) 否则,算法使用称为信息增益的基于熵的度量作为启发信息,选择能够最好地将样本分类的属性(步骤6)。该属性成为该结点的“测试”或者“判定”属性(步骤7)。所有的属性都是分类的,即离散值。连续属性必须离散化。
4) 对测试属性的每个已知的值创建一个分枝,并据此划分样本(步骤8-10)。
5) 算法使用相同的过程,递归形成每个划分上的样本判定树。一旦一个属性出现在一个结点上,就不必该结点的任何后代上考虑它(步骤13)
递归划分步骤仅当下列条件之一成立停止:
a.给定结点的所有样本属于同一类(步骤2,3)
b.没有剩余属性可以用来进一步划分样本(步骤4)。在此情况下使用多数表决(步骤5)。这涉及将给定的结点转化为树叶,并用样本中的多数所在的类标记它。
c.分枝 test_attribute = a,没有样本(步骤11).在这种情况下,以samples中的多数类创建一个树叶(步骤12)
2.4 其他算法
C4.5 :Quinlan
Classification and Regression Tress(CART): (L.Breiman,J.Friedman,R,OIshen,C,Stone)
共同点:都是贪心算法,自上而下
不同点:属性选择度量方法不同:C4.5(gain ratio),CART(gini index),ID3(Information Gain)
对于连续性变量的属性采用离散化处理
3. 树剪枝叶(避免overfiting)
3.1 先剪枝
3.2 后剪枝
4. 决策树的优点
直观、便于理解、小规模数据集有效
5. 决策树的缺点
处理连续型变量不好
类别较多时,错误增加的比较快
可规模性一般