从负指数分布/泊松分布到排队论(经理能扣篮，但不经常也不绝对)

从经理穿着皮鞋能不能扣篮，引起了一段思考。

周六上午在家带娃，我已经快崩溃，所以作文时间放在了午后。

假如你相信上帝真的是在掷骰子，那么我们的世界就是上帝的一系列实验生成的。
假如你相信世界是二元元素的组合，那么使用二进制便可以完整描述整个世界。

一切从二项分布开始裂变。

---

二项分布

让我们看一道非常简单的概率统计习题：
如果做一次实验，一个独立的事件$E$发生的概率是$p$，那么请问，连续做$n$次实验，让事件$E$发生$k$次的概率是多少？

非常简单的习题，只要知道独立事件同时发生的概率相乘性质即可解题。

1. 单次事件发生的概率就是$p$，单次事件不发生的概率是$1-p$
2. 事件发生$k$次的概率就是$p^k$
3. 实验进行了$n$次，$k$次发生了事件，意味着$n-k$次没有发生事件
4. $n-k$次没有发生事件的概率是$(1-p{)}^{n-k}$
5. 事件的发生与实验顺序无关，故发生$k$次的可能性有$C_n^k$种

综上1～4，连续做$n$次实验，事件$E$发生$k$次的概率为：

$P(X=k)=C_n^k\times p^k\times (1-p{)}^{n-k}$

是的，这就是 二项分布 。

根据以上的二项分布，我们可以计算出在$P(X=k)$的概率下，重复实验$k$次，事件发生的 平均次数 为：

$\lambda =n\times p$

---

现在让我们来看所谓的 事件 以及 平均次数 的具体意义和性质。

对于在推导二项分布时的我们理解的事件，都是 单次等概率的事件。 即做一次实验，事件发生的概率是相同的，也就是定值$p$，比如抛硬币。利用这类事件，我们已经非常容易地推导出二项分布的式子。

但是还有一种事件，固定的时间内它们发生的 次数 与单次实验事件发生的概率是无关的，而是与连续的时间段或者连续的空间大小有关，即 单位时间/空间内时间发生的次数平均值为定值。 典型的例子就是生产线产品的良品率，无论你用多少条相同的生产线做实验，良品率总是相等的。本文接下来要讨论的所有事件，均是此类事件。

此类事件具有 累加性质 。即 事件在一个连续的时间段或者空间中持续以某种概率发生。

这种事件很难对应到 二项分布 的所谓独立实验重复多次的场景，我们不妨先借用一下$\lambda =n\times p$这个式子，从事情的本初开始。

---

负指数分布

再看一遍 一段时间内事件发生平均次数 的式子：

$\lambda =n\times p$

如果$\lambda$为定值，即在确定的区间内，无论做多少次实验，都不会改变实验成功的次数，我们换一种写法：

$p=\lambda \times \frac{1}{n}$

即 事件发生的概率与$\frac{1}{n}$成正比！ 至于$\frac{1}{n}$如何被解释，我们接着往下看。

如果我们把所谓的 单位时间 规约为1，那么$\frac{1}{n}$就是一个小的时间片，整个单位时间被分成了等大小的$n$份，$n$越大，时间片就越小，我们在单位1的约束下，不妨将$\frac{1}{n}$看作是$\Delta t$，那么$p$就是$\Delta t$内事件发生$k$次的概率：

$P_k(\Delta t)=\lambda \Delta t$

即 事件发生的概率与时间片的长短成正比！

但是发生几次呢？至少发生1次！也可能发生2次，3次，5次，100次。可是，如果发生次数大于1次，在后面的推导中，便无法拟合二项分布的含义，如何将发生的次数限制在至多1次呢？

答案是 将$\Delta t$想象成非常小，即发生1次事件的概率都超级小，更何况多次。

所以，在$\Delta t$非常小的保证下，我们认为$P_k$可以表达成下面的式子：

$P_k(\Delta t)=P_1(\Delta t)+o(\Delta t)=\lambda \Delta t$

我们将发生事件大于1次的概率看作是一个关于$\Delta t$高阶无穷小。反正后面我们采用微积分推导时必然保证$\Delta t$趋向于$0$，因此高阶无穷小是可以忽略的。

我们忽略高阶无穷小后，有：

$P_1(\Delta t)=\lambda \Delta t$

接下来，按照概率的定义，在$\Delta t$内事件不发生的概率就是：

$P_0(\Delta t)=1-\lambda \Delta t$

我们将其形式化：

$P_0(t)=1-\lambda t$ 【式子1】

注意，虽然我们为了形式化将$\Delta t$换成了$t$，但是这只是为了数学上推导方便，我们必须记住，自变量$t$是时间片的长短，而不是一个绝对时间！那么按照$P_0(t)$的解释，$P_0(t+\Delta t)$的意思就是 时间片长度为$t+\Delta t$时事件不发生的概率！

请注意，长度为$t+\Delta t$的时间片可以分割为连续的两个小时间片$t$和$\Delta t$， 时间片$t+\Delta t$中不发生事件的概率要求时间片$t$和时间片$\Delta t$中均不发生事件！ 按照概率相乘的原理：

$P_0(t+\Delta t)=P_0(t)P_0(\Delta t)$ 【式子2】

代入式子1，我们整理式子2：

$P_0(t+\Delta t)=P_0(t)(1-\lambda \Delta t)=P_0(t)-\lambda \Delta t{P}_0(t)$

稍微变换一下：

$\frac{P_0(t+\Delta t)-P_0(t)}{\Delta t}=-\lambda P_0(t)$ 【式子3】

式子3是什么？取极限不就是个求导吗：

${\lim }_{\Delta t\to 0}\frac{P_0(t+\Delta t)-P_0(t)}{\Delta t}=P_0\prime (t)=-\lambda P_0(t)$

写成微分方式：

$\frac{d(P_0(t))}{P_0(t)dt}=-\lambda$

两边同时积分，按照第一类换元积分：

$\int \frac{d(P_0(t))}{P_0(t)dt}dt=\int \frac{1}{P_0(t)}d(P_0(t))=lo{g}_e{P}_0(t)=-\lambda t+C$

取$e$的指数得到：

$P_0(t)=e^C\times e^{-\lambda t}$

$t$是一个时间片，$t=0$就是无，当然不会有任何事件发生，即$P_0(0)=1$，即：

$P_0(t)=e^{-\lambda t}$

在时间片长度为$t$的时间内不发生事件的概率是$e^{-\lambda t}$，那么至少发生1个事件的概率就是：

$P_1(t)=1-e^{-\lambda t}$

这就是概率积累函数，这不就是 负指数分布 吗？即 单位时间内时间发生平均次数为固定值$\lambda$的事件的时间间隔的概率为负指数分布！

---

泊松分布

再看一遍 一段时间内事件发生平均次数 的式子：

$\lambda =n\times p$

这里，我们依然假定$\lambda$为定值。这个是本文通篇的假定。

在推导负指数分布的时候，我们已经将单位时间分割成了要多小有多小的$\Delta t$，并且我们还知道，这些小的时间片$\Delta t$内发生1次以上事件的概率为$\Delta t$的高阶无穷小，在参与取极限，微积分等数学运算的时候是被忽略的，于是我们得到了非常清爽的式子：

$P_1(\Delta t)=\lambda \Delta t$

我们将其形式化：

$P_1(t)=\lambda t$

注意，自变量$t$是一个时间段，而不是绝对时间，这里再次强调。

好了，开始我们的推导。

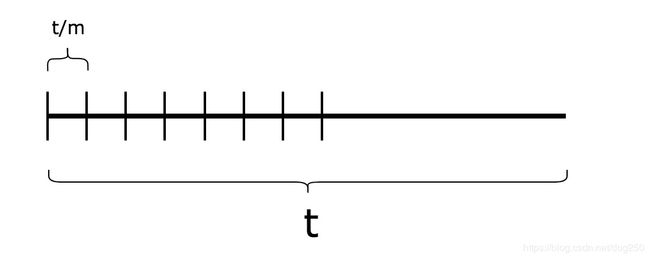
现在我把这个已经非常小的时间片$t$（也就是$\Delta t$，只是写成$t$好看一些）画出来：

我们终于可以套用 二项分布中的实验模型 了。

• 在$t$时间片内，发生了一次事件。

我们知道$t$已经非常小，小到可观测范围只能发生1次事件，发生1次以上事件的概率微乎其微(高阶无穷小$o(t)$)，然而，由于时间片是连续的，即便再小它依旧是 继续可分的 ，像分形一样，我们把$t$放大，将其再等分成$m$份：

之所以将$t$再继续等分$m$份是因为，我们知道$t$时间片内事件发生的概率是$\lambda t$，那么在$t$时间片内，如果事件发生了，那么事件具体在哪一个更精细的时间片内发生，又是一个概率问题：

1. 是在第1个$\frac{t}{m}$时间片里发生吗？
2. 是在第2个$\frac{t}{m}$时间片里发生吗？
3. 是在第3个$\frac{t}{m}$时间片里发生吗？
4. …是在第$m$个$\frac{t}{m}$时间片里发生吗？

到底再哪个小时间片里发生呢？很简单，都有可能发生。都是等概率的，每个小时间片发生事件的概率均为$\frac{1}{m}$，按照概率相乘的规则：

• 事件在$t$事件片发生的概率为$\lambda t$
• 事件如果真的在$t$时间片发生，那么它在某一个$\frac{t}{m}$小时间片发生的概率就是$\lambda t\times \frac{1}{m}$

是的，概率就是

$P=\lambda t\times \frac{1}{m}$

哈哈，为了得到概率分布，我们可以做实验了：

• 连续做$k$次实验，$k<m$，每次实验事件发生的概率是$\lambda t\times \frac{1}{m}$

这就是一个典型的二项分布：

$P(X=k)=C_m^k\times (\frac{\lambda t}{m}{)}^k\times (1-\frac{\lambda t}{m}{)}^{m-k}$

现在事情可以开始了。

由于时间是连续流逝的(空间也一样)，那么时间片就是无限可分割的，我们求一个连续变量下事件发生的概率，需要就是将时间片(或者空间) 无限分割 。

以上这个式子里，其实$t$已经是无限分割的结果了，但是我们不要在乎$t$，只需知道在$t$时间片里至多发生1次事件就好了，重要的是， 我们将$t$分割$m$份，让$m$趋向于无穷大会怎样？

求极限：

${\lim }_{m\to \infty }{C}_m^k\times (\frac{\lambda t}{m}{)}^k\times (1-\frac{\lambda t}{m}{)}^{m-k}$

直接求解即可，其中只需要应用一个重要极限公式，一切迎刃而解：

${\lim }_{m\to \infty }(1-\frac{\lambda t}{m}{)}^m={\lim }_{m\to \infty }(1-\frac{1}{\frac{m}{\lambda t}}{)}^{\frac{m}{\lambda t}\lambda t}=e^{\lambda t}$

直接写答案吧：

$P(X=k)=\frac{e^{-\lambda t}(\lambda t{)}^k}{k!}$

这是什么？这就是 泊松分布。

即 单位时间内时间发生平均次数为固定值$\lambda$的事件在单位时间内发生的次数符合泊松分布！

---

所以说，负指数分布和泊松分布是一回事。它们两个均可以从 单位时间内时间发生平均次数为固定值$\lambda$ 这个大前提推导出来。

---

生灭过程和排队

有来必有往，有去必有回。

我们为所谓的事件赋予其意义。

把单位时间发生的事件的看作 请求的到达 ，那么， 请求被处理 自然也可以被看作是同类的事件。

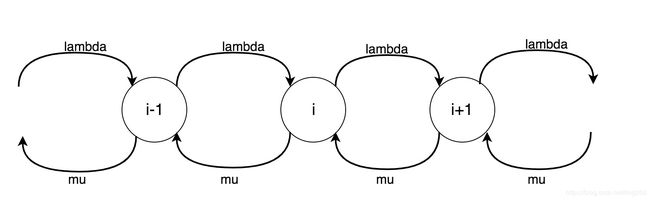
请求不断地到达，又不断地被处理，这是一个马尔可夫过程，最终这个过程就形成了一个马尔可夫链，每一个状态，我们可以看作是 未被处理请求为$i$的概率 ：

由于请求的到来和被处理均是统计分布，那么统计意义的突发必然会造成排队，即上述的马尔可夫过程必然向后延展，然而如果系统是稳定的，积压的请求将会在突发空闲期被持续处理，从而使得马尔可夫过程向前收缩，最终对于每一个状态而言，都将达成一个平衡：

$P_{i-1}\lambda +P_{i+1}\mu =P_i\lambda +P_i\mu$

此外，系统中所有的状态的概率之和恒等于$1$：

${\Sigma }_{i=0}^n{P}_i=1$

此外，对于状态$0$，它没有前置状态，所以必然有：

$P_0\lambda =P_1\mu$

我们用此而递推：

$P_0\lambda +P_2\mu =P_1(\lambda +\mu )$
$P_1\lambda +P_3\mu =P_2(\lambda +\mu )$
$P_2\lambda +P_4\mu =P_3(\lambda +\mu )$
$...$
$P_i\lambda +P_{i+2}\mu =P_{i+1}(\lambda +\mu )$

上面所有式子整理，得到：

$P_i=(\frac{\lambda }{\mu }{)}^i{P}_0$

进一步：

${\Sigma }_{i=0}^n{P}_i=P_0{\Sigma }_{i=0}^n(\frac{\lambda }{\mu }{)}^i=1$

数列求和而已：

$P_0\frac{\mu }{\mu -\lambda }=1$

嗯，这样就求出了$P_0$：

$P_0=1-\frac{\lambda }{\mu }$

那么$P_i$自然也求出来了：

$P_i=(1-\frac{\lambda }{\mu })(\frac{\lambda }{\mu }{)}^i$

接下来，排队论基础中的典型结论基本就都能出来了：

• 平均排队实体数量
  $N_{avg}={\Sigma }_{n}n{P}_n=\frac{\lambda }{\mu -\lambda }$
• 平均等待时延
  $T_{avg}=\frac{N}{\lambda }=\frac{1}{\mu -\lambda }$.
• …

现在公式都可以非常简单明确地根据泊松分布，负指数分布推导出来了，但是问题是， 你真的相信世界上的一些事情符合泊松分布吗？或者说，即便你相信它们符合，它们真的符合泊松分布吗？

如果是，那么上面的公式就可以描述一切，如果不是，怎么办？

---

泊松分布/排队论的适用性

基于泊松分布/负指数分布的排队论不适用任何现实场景！！

因为现实中根本就没有什么事件规律符合泊松分布。

我们以为路面某个监测点的车辆的到达符合泊松分布，但是非也！几乎可以肯定，人是喜欢跟风的，这意味着车辆到达某个点并非独立事件，这也是交通拥堵的根本原因。

我们以为互联网交换节点数据包的到达符合泊松分布，但是非也！数据包确实具有突发性达到的特征，但是前后两个数据包之间关联着巨大的粘性，它们并非独立到达的。这也是我在2014年设计状态防火墙cache的依据，利用局部性嘛。

之所以泊松分布的结论被如此普遍地被利用，完全在于 其在数学上非常容易处理，容易预测后事。 然后我们利用现实的参数，给予矫正，即可得到相当不错的结论。

其实仔细想想，世界本应该就是泊松分布主宰的，所谓的跟风和粘性，那可能是人性使然。路面上车里的司机，你不认识我，我也不认识你，大家却往同一条路上走，如果不是 我相信别人有更好的选择 ，那么就是别无选择了…对了，上下班高峰，节假日，天气，也会让泊松分布失效。但这些说来说去还是因为人为原因导致，比如人都是白天才出门，晚上则闭户。所以说，你要把事件尺度拉大，在以年为单位时间的范围，或者更长的单位1，泊松分布将会越离越拟合现实。

---

单队列和多队列的问题

存在多个服务台的情况下，到底是单队列效率高还是多队列效率高？

这个我们来算一下。

M/M/1情况下，单队列，排队实体的平均等待延时为：

$T_{single}=\frac{1}{1\times \mu -\lambda }$.

如果队列被分成了$N$个，那么单位$1$作用于每一个队列则为$\frac{1}{N}$，而平均到达率对于每一个队列，均将是$\frac{\lambda }{N}$，平均等待时间，代入上式：

$T_{multi}=\frac{1}{(\frac{1}{N})\times \mu -\frac{\lambda }{N}}=N\times T_{single}$

很遗憾，有点有悖于常识，如果采用多队列，平均等待时间将会延长！这就是为什么对于以太网这种统计复用的突发流量网络而言，并没有采用任何XDM（X可为时间，频率…）的策略，而只是采用了时间域上单队列退避的CSMA/CD策略的原因！

然而，比如以Linux内核而论，进程调度， 却是多队列的，每CPU核心一个队列，这是Why？这是因为，相比于进程的到达和被调度，锁以及cache miss的开销更大，这纯粹是一个实现上的工程优化，不伤排队论的大雅，和算法无关。

经理能不能扣篮

经理穿着皮鞋能扣篮吗？我觉得能。

经理能扣篮，但不经常，也不绝对。

这就跟总有那么一个非零的概率，一个立方的空气分子全部朝着一个方向运动是一样的道理。

经理能扣篮，这只是一个概率性的结论，经理能扣篮并不意味着经理扣篮就一定能成功。

---

浙江温州皮鞋湿，下雨进水不会胖。