第十三章 图像的几何变换之旋转

旋转，在几何变换中属于比较复杂的算法。因为旋转算法无法离开旋转方程。先进行旋转方程的推导吧。这个是初中的知识。复习一下。

 

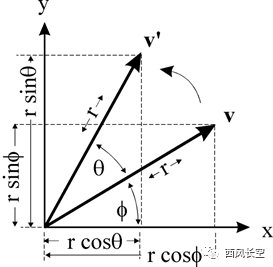
如图所示，点V绕原点旋转θ角，得到V’.假设V点的坐标是x,y.则V到原点的距离是R .它的角度是ϕ。则

X= Rcos(ϕ)    Y = Rsin(ϕ)

V’旋转θ 的

X’ = Rcos(ϕ+θ);  Y’ = Rsin(ϕ+θ);

展开后得

x’=rcosθ cosϕ -rsinθ cosϕ  代入后得

X’=xcosθ -ysinθ 

Y’=xsinθ+ycosθ;

这个是直接旋转的方程。

同样下图是直接旋转后的结果图。

 

对于旋转，有两个细节。需要解决。第一，一般情况下，我们旋转是通过A旋转后得到B。但是由于旋转是基于浮点数操作，或者说是基于非整数系数运算，但到结果成像素时又是整数，会舍弃掉一部分数据，所以一般情况下直接A旋转后得到B会造成图像跳点。第二，由于旋转后会偏离中心，所以我们会对图像进行半长半宽的反向移位以保证正确性。如上图所示。

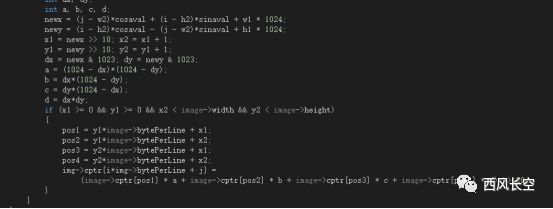
正确的做法是由结果推导取源图像中的像素混合运算。公式不变，但数据变了。正确的运算结果是：

 

    下面针对两种算法贴上代码：

PStruImage ImageRotateDirect(PStruImage image, float angle)

{

#define RADIAN3.1415926

int width = image->width;

int height = image->height;

float newwid, newhei;

int i, j;

int w1, w2, h1, h2;

float sinaval = 0;

float cosaval = 0;

 

PStruImage img;

sinaval = sin(angle *RADIAN /180);

cosaval = cos(angle *RADIAN /180);

if (angle < 0)

{

newwid = width*cosaval - height*sinaval + 0.5;

newhei = width*sinaval + height*cosaval  +0.5;

}

else

{

newwid = width*cosaval + height*sinaval + 0.5;

newhei = width*sinaval + height*cosaval + 0.5;

}

img = CreatImage(abs((int)newwid), abs((int)newhei), image->nchannels);

w1 = width /2;

h1 = height/2;

w2 = newwid/2;

h2 = newhei/2;

for (i = 1; i

{

for (j = 1; j < width; j++)

{

float newx, newy;

int x1, y1, x2, y2;

int pos1, pos2, pos3, pos4;

float dx, dy;

int a, b, c, d;

newx = (j-w1)*cosaval - (i-h1)*sinaval+w2;

newy = (i-h1)*cosaval + (j-w1)*sinaval+h2;

x1 = (newx); x2 = x1 + 1;

y1 = (newy); y2 = y1 + 1;

if (x1 >= 0 && y1 >= 0 && x2 < img->width && y2 < img->height)

{

img->cptr[y1*img->bytePerLine + x1] = image->cptr[i*image->bytePerLine + j];

}

}

}

return img;

}

对于正确的离解算法的代码我就只贴关键部分的图了.

上面算法进行了嵌入式级的优化。

源代码： https://download.csdn.net/download/finger157959/12528142