LZW编码的学习与实现

大家好，现在是2020年5月19日，不知不觉5年过去了，看到最近还有很多人评论我的这篇文章，非常的开心和满足，显然我写这篇文章所做的微小贡献帮助到了一些人。今天我从头到尾再看了一遍我写的东西，还是有一些东西没有描述清楚，比如下面第一个表里里面，dictionary 那一列里面的 xx:5，我就一直没明白什么意思。另外，一些朋友在评论区对256，257是怎么来的感到疑惑，我都会对文章做一次修订，将这些内容描述清楚，谢谢大家。

Preface

看了一天，感觉终于搞明白了一点（代码终于写对了），编码过程大四的时候学过一点点，按部就班的按照步骤来做就行了，解码过程貌似课堂上老师没讲，自己看wiki上的讲解和example搞懂了。

LZW全称Lempel–Ziv–Welch，就是这个三个人搞出来的。

LZW的工作思路，考虑一段数据，abcabcabc，对于这样的一段数据，如果不做任何处理和压缩，假设每个字符用一个字节来表示，直接存储的空间应该是9字节。详细说明下：
下表是我们dictionary，也就是码表，字符与编码的对应。

character	decimal	binary
a	1	0000 0001
b	2	0000 0010
c	3	0000 0011

---

观察上面的字符串，发现abc是重复的，如果abc能用一个字节来表示的话，那么，只需要3字节存储就足够了。

character	decimal	binary
abc	1	0000 0001

---

OK，LZW就是这个尿性，它就是想这么搞。

Encoding

基本思想

编码的基本思想是这样的，首先我们有一个码表或者称为dictionary，里面只定义单个字符和编码，比如0-9a-zA-Z这些，其实ASCII码中的所有全部都放进去都可以。

也就是说通常用十进制数0-255来表示单一字符（single character）。

然后我们开始读取字符串，很显然对于任何常规字符串，每个single character都可以得到一个码字，但是如果我们不做处理的话，那么n个字符encode后，就是n个码字了完全没有压缩。

所以，再边读取的时候，一边开始对dictionary进行扩增，不断的将single character拼接成dictionary中不存在的符号（symbol），扩充dictionary，这样下次再次遇到这样的组合，就可以使用有一个码字表示了。

流程

说实话，用纯文字描述还真的不是很好描述，于是我画了一个流程图来描述这样一个过程。

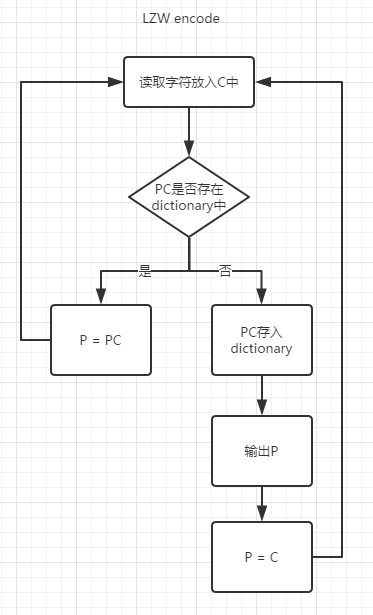
就是上面这个图了，代码只要照着这个写就能搞定问题。但出于尊重，还是要讲解下比较好。
首先我们需要两个暂存器，P和C，为啥叫这个名字呢。（当时上学那会，老师给的是p和s，完全不知道意义）

P -> Previous -> 表示之前的字符
C -> Current -> 表示当前读取的字符

然后我们考虑字符串abcbcabcabcd

来，按步骤演算一下：

首先我们需要一个dictionary，简单考虑，只考虑a-d，4个英文小写字母吧。这里想表达的意思是，整个宇宙全世界只有a-d 4个英文字母，我们的ascii表中也只有 4 个字母。

symbol	decimal
a	1
b	2
c	3
d	4

---

下面是演算过程：
注意下面 dictionary 中的冒号后面的数字，表示的新的ascii码，啥意思呢？上面说了，全世界只有 a-d 4个字母，码表是 1-4，接下来我们要将 ab 两个字母连在一起作为一个整体，用 5 来给它编码，因此就是 ab:5

step	P	C	is PC in dic	output P	dictionary(符号:编码)	description
1	NULL	a		初始化，不处理
2	a	b	no	1	ab:5	ab不存在dictionary中，扩充
3	b	c	no	2	bc:6
4	c	b	no	3	cb:7
5	b	c	yes			bc在dictionary中，P = PC
6	bc	a	no	6	bca:8
7	a	b	yes
8	ab	c	no	5	abc:9
9	c	a	no	3	ca:10
10	a	b	yes
11	ab	c	yes
12	abc	d	no	9
13	d	NULL		4		结束

---

经过上面的演算过程，我们的dictionary也扩展为：

symbol	decimal
a	1
b	2
c	3
d	4
ab	5
bc	6
cb	7
bca	8
abc	9
ca	10

---

代码实现

最后贴下自己实现的代码：

    public static List<Integer> encode(String data) {
        List<Integer> result = new ArrayList<>();
        
        //初始化dictionary
        int idleCode = 256;
        HashMap<String, Integer> dic = new HashMap<>();
        for (int i = 0; i < 256; i++) {
            dic.put((char)i + "", i);
        }
        
        String previous = "";
        String pc = "";
        for (char c : data.toCharArray()) {
            pc = previous + c;
            if (dic.containsKey(pc)) {
                previous = pc;
            } else {
                dic.put(pc, idleCode++);
                result.add(dic.get(previous));
                previous = "" + c;
            }
        }
        
        //最后一次输出
        if (!previous.equals("")) {
            result.add(dic.get(previous));
        }
        
        return result;
    }

Output

//abcbcabcabcd
[97, 98, 99, 257, 256, 99, 260, 100]

256, 257 是怎么来的？

上面用表格模拟整个过程的时候，是假设全世界只有4个字符，ASCII码表的大小也只有4个字符，但是上面这会程序运行时，我们的世界又是真实世界了，ASCII表示有256个字符的，编码范围从0到255。那么我们新创造的字符用什么来编码呢？当然是从 255 后面开始追加了。

Decoding

主要思想

解码的主要思想是，一个编码序列，我们也是事先知道一个固定的码表，我一边读取码字，一边输出解码后的字符，同时一边扩充码表。这个我也觉得好难用用文字表达清楚，上流程图。

流程

同样的，这里给出一个编码序列

[97, 98, 99, 257, 256, 99, 260, 100]

首先我们需要一个默认的dictionary。

decimal	symbol
97	a
98	b
99	c
100	d

---

接下来是演算过程：

Input	P	C	is C in dic	output	dictionary	description
97	NULL	a	yes	a
98	a	b	no	1	ab:5	ab不存在dictionary中，扩充
99	b	c	no	2	bc:6
257	c	b	no	3	cb:7
256	b	c	yes			bc在dictionary中，P = PC
99	bc	a	no	6	bca:8
260	a	b	yes
100	ab	c	no	5	abc:9

代码实现

    public static String decode(List arr) {
        
        StringBuilder result = new StringBuilder();
        int idleCode = 256;
        HashMap dic = new HashMap<>();
        for (int i = 0; i < 256; i++) {
            dic.put(i, (char)i + "");
        }
        
        String p = "";
        String c = "";
        
        for (int code : arr) {
            if (dic.containsKey(code)) {
                c = dic.get(code);
            } else if (code == idleCode) {  //这里唯一的情况是 aaaaaaa
                c = c + c.charAt(0);
            } else {
                System.out.println("bad encode");
            }
            
            if (!p.equals("")) {
                dic.put(idleCode++, p + c.charAt(0));
            }
            result.append(c);
            p = c;
        }
        
        return result.toString();
    }

Summary

References

1. Lempel–Ziv–Welch from Wikipedia.
2. LZW的各种语言的实现
3. ASCII