数据结构有关树的知识总结(二)
这一篇文章主要介绍三个知识点:哈夫曼树、堆排序以及最佳归并树和败者树。
(四)哈夫曼树
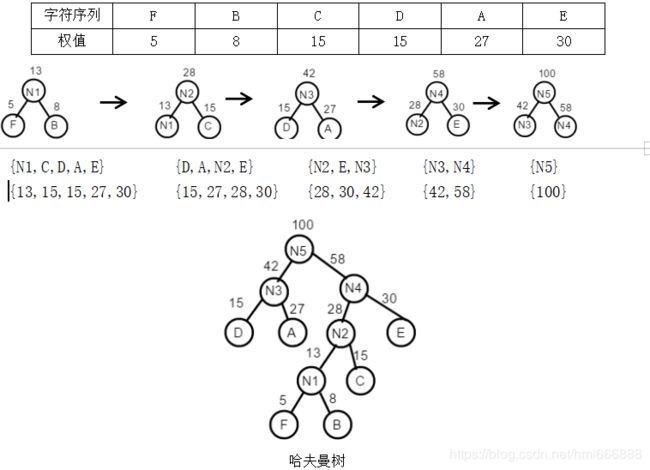
1、构造哈夫曼树:
哈夫曼树的特点:①权值越大,离根节点越近;②树中没有度为1的结点,成为正则(严格)二叉树;③树的带权路径长度(WPL)最短。
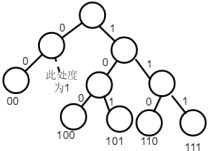
2、哈夫曼编码:
应用于平常的压缩文件,是最基本的压缩编码。其原理是:如在网上发送文件在计算机中需要将文件中的字符转化成计算机语言(01语言),根据发送的文件中每个字符出现的频率(即权值)构造哈夫曼树,左树为0,右树为1,从而可以很有效地压缩文件。
注:哈夫曼编码是前缀码编码,过在解码时不会出现歧义。
前缀编码:每一个字符转化成01语言后,都不是文件中的任何其他字符的前缀(如:A:0,B如果是00,则出现歧义,在解码时00不知该解码为AA还是B,这就不是前缀编码)
原因:因为哈夫曼树中,任意字符都只出现在叶结点,通往任一叶结点的路径都不可能通往其他叶结点,所以每个字符的编码都是唯一的,而且解码的过程是一次次从根节点走向叶结点的过程。
3、关于哈夫曼树的有关题目与解答:
- 根据使用频率为5个字符设计的哈夫曼编码,不可能是(C)
A.111,110,10,01,00 B.000,001,010,011,1 C.100,11,10,1,0 D.001,000,01,11,10
解:哈夫曼编码是前缀编码,C选项100,是10的前缀
2.假设哈夫曼二叉树只有0度和2度结点,根据使用频率为5个字符设计哈夫曼编码,则00,100,101,110,111为什么不可能是其编码?
3.设有13个值组成一棵哈夫曼树(正则二叉树),则哈夫曼树共有 25 个结点(叶结点数=2度结点数+1)
4.假设哈夫曼树只有0度和2度结点,有n个叶结点的哈夫曼树总结点为 2n-1 个。
5.从任意一结点出发到根的路径上所经过的节点序列按其关键有序的是(D)
A.二叉排序树 B.平衡二叉树 C.哈夫曼树 D堆
解:①二叉排序树和平衡二叉树都是中序有序,左<跟<右;②而哈夫曼树每次合并构成新的节点,根节点是其两个儿子结点的权值之和,只有当权值全为正数时才成立;③对要求父节点要比儿子节点都要大(小),所以从任意结点出发到根结点的过程,都死由小到大(或由大到小)有序的。
(五)堆排序
特点:
①堆的数据结构是完全二叉树。
②大根堆、小根堆(大顶堆、小顶堆):根的值比左右儿子节点的值都大(小)
③排序思想:将一个无序的序列调整为一个堆,就可以找出这棵树的最大(最小值),然后递归进行排序。
④堆与优先级树相似,都要求根结点要比左右儿子结点要大(小)(14年考到过一次)。
⑤时间复杂度:O(nlog₂n)
⑥空间复杂度O(1):空间复杂度与问题的规模、算法输入、以及算法函数本身有关
⑦从根结点到任意叶结点(从任意叶结点到根节点)所经过的结点是有序的
⑧适用于关键字很多的场景,典型的例子就是,从10000个关键字中选出10个最小的,这种情况用堆排序最好。
与优先级树对比:
·约定优先值低的优先级高
·优先级树每个结点存储一个元素
·根节点的优先级大于(或小于)其儿子结点,即越接近根节点优先级越高
·根节点优先级高于儿子结点,则成为极大优先级树,反之成为极小优先级树。
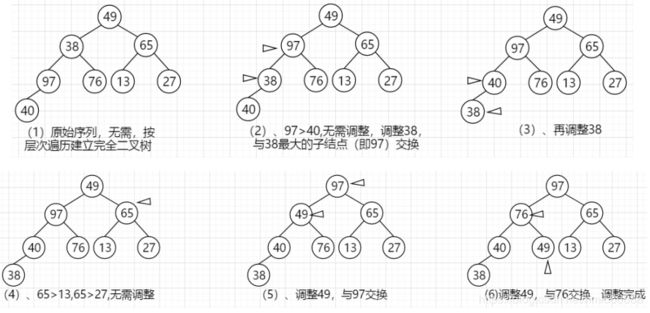
1、堆的创建
例如:序列{49,38,65,97,76,13,27,40}
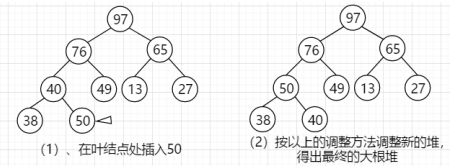
2、堆的插入
堆的插入如完全二叉树的插入一般,只能在叶子节点上插入,并重新调整新的堆:
3、堆的删除
如:删除97,一直往以97为根的左子树走,若最小左子树有右儿子r,则将97交换与r交换,若最小左子树只有左儿子L,则将97与L交换。反正是交换到最后面的叶子结点
(六)最佳归并树、败者树
1、最佳归并树:
1、特点:①属于外部排序;
②其实就是k叉哈夫曼树;
③每个记录(结点)都需要进行两次I/O操作;
④可算出所有结点代表的归并段总的I/O操作数=书的带权路径长度。
2、例题:由置换-选择排序的出9个对归并段,其长度(记录个数)依次为:9,30,12,18,3,17,2,6,24。
首先,记录个数进行排序得:{2,3,6,9,12,17,18,24,30}
然后,建立3叉哈夫曼树:(计算带权路径长度时只计算叶结点即可)
2、败者树
1、特点:①k路归并败者树的高度h=[log₂k]+1(向上取整,注:高度不包括最上层选出的结点),选出最值需要log₂k次。
②建树时间复杂度:O(klog₂k),取最值时间复杂度:O(log₂k),空间复杂度O(1)
③排序思想:想用一个较大的时间复杂度将待排序的关键字简称一颗满足要求的树,从中取出一个关键字时,将新的关键字放在刚取出的关键字的位置,如此只会在一点上对树的结构造成破坏,不会影响全局,只需花较小的时间复杂度进行局部调整,恢复结构,从而降低时间复杂度。(这是所有有关树的排序的精髓)。简单来说:
建树——>插入、删除——>局部调整,恢复结构。
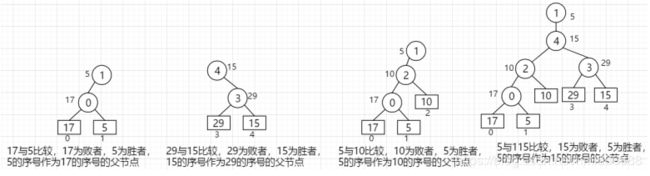
2、建立败者树:
设5个有序归并段:F0{17,21,...} F1{5,44,...} F2{10,12,...} F3{29,32,...} F4{15,56,...},依次取各归并段的第一个记录:
17,5,10,29,15;对应序号为0,1,2,3,4
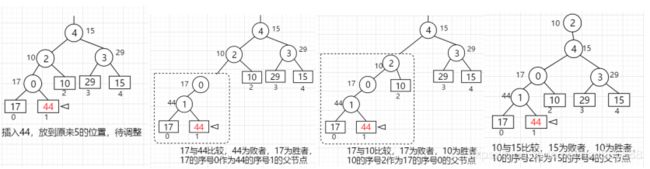
3、调整败者树:
取出上述所得最小值5,用F1归并段中5的下一个关键字放在原来5的位置,再进行调整。