public static double Atan2(double y,double x)
Parameters(参数):
- The y coordinate(坐标) of a point(点).
- The x coordinate of a point.
Return Value
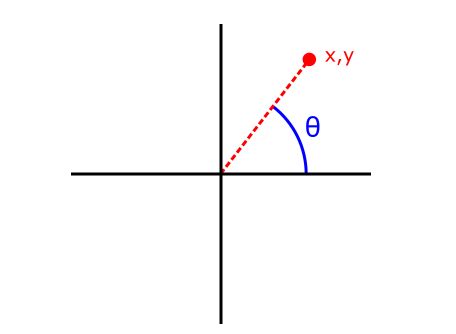
An angle, θ, measured in radians(以弧度来计量), such that -π≤θ≤π, and tan(θ) = y / x, where (x, y) is a point in the Cartesian plane(笛卡尔平面).
Observe the following(观察如下:)[实际就是atan2实现细节]
- For (x, y) in quadrant(象限) 1, 0 < θ < π/2.
- For (x, y) in quadrant(象限) 2, π/2 < θ≤π.
- For (x, y) in quadrant(象限) 3, -π < θ < -π/2.
- For (x, y) in quadrant(象限) 4, -π/2 < θ < 0.
For points on the boundaries(边缘或分界线) of the quadrants(象限), the return value is the following:
- If y is 0 and x is not negative(不为负), θ = 0.
- If y is 0 and x is negative, θ = π.
- If y is positive(为正) and x is 0, θ = π/2.
- If y is negative and x is 0, θ = -π/2.
- If y is 0 and x is 0, θ = 0.
If x or y is NaN(not a number,不是一个数值), or if x and y are either(要么是) PositiveInfinity(正无穷大) or (要么是)NegativeInfinity(负无穷大), the method returns NaN.
This is the counterclockwise(逆时针) angle.
专业词汇区别:
- Parameter: 形式参数(函数声明中的参数)
- Argument: 实际参数(函数调用时的参数)
下面扩展是因为和参数关系比较密切(其实和类型更密切):
扩展一下,什么是函数签名(the function’s signature)
强类型语言中,函数签名是非常重要的一个概念,那么
提问: 函数签名包括那些内容呢?
回答: 除了函数名之外的任何东西
例如: double Atan2(double y,double x)
签名包括:
- 函数的返回值类型(double)
- 函数的参数个数(2个)
- 函数的参数类型(2个都是double)
- 函数的参数的顺序位置(不能顺序错误)
- 如果是c/c++的话,还可能包括函数的调用规范
其实回调函数就是函数签名的一个经典应用场合。
重点句型及扩展:
- either....or....: 要么.....要么.....(两者选其一)
- neither...nor...: 即不是....也不是....(两者都否定)
- not only...but also...: 不但...而且...(两者都为肯定)
如果这三句不放在一起讲解,那肯定不是个好老师,哈哈!
与atan区别:
与 atan 的不同,atan2 比 atan 稳定。
如:atan(y/x),当 y 远远大于 x 时,计算结果是不稳定的。
atan2(y,x)的做法:
当 x 的绝对值比 y 的绝对值大时使用 atan(y/x);
反之使用 atan(x/y)。
这样就保证了数值稳定性。
这三天,分享了三角函数sin/cos/atan2这三个基础重要的函数,因为只要这三个函数,就能解决经典的2D朝向正确的位移功能。
上面就是sin/cos/atan2的应用。当然还有高效的矢量法及矩阵法。但是三角函数的确是最基础最基础的解决方案。其他方案都是从三角函数开始更高层次的公式推导而来。
其实你会发现一个有趣的事实,当你学了矢量数学,你会觉得经典牛顿力学的计算会方便快速高效很多,而当你学了导数后,高中时令人头疼的极值问题迎刃而解。
但是不管如何,只有一步一步,踏踏实实的学习才能有进步不是。
顺便提一下,关于参考文档,我个人偏好微软的MSDN。