数据结构(C):以临接矩阵存和邻接表存储的无(有)向图的深度和广度遍历(附完整代码)
1.深度优先遍历
思想:
①从图中某个顶点V0 出发,访问此顶点。
②依次从V0的各个未被访问的邻接点出发深度优先遍历图, 直至图中所有和V0有路径相通的顶点都被访问到。
③若图中还有顶点未被访问(非连通图),另选图中一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
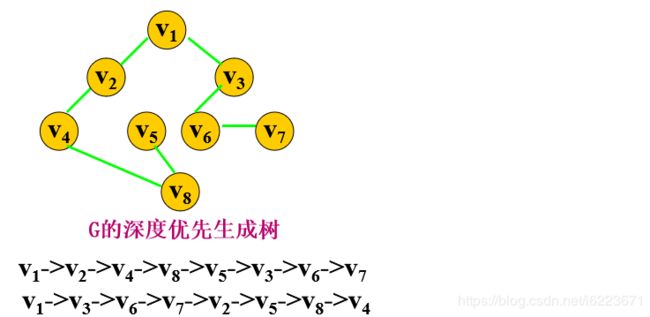
注:虽然由图形得出的深度遍历序列不唯一,但是对于给定的存储结构深度遍历序列唯一。如:
在遍历图时,对图中每个顶点至多调用一次DFS函数,因为一旦某个顶点被标志成已被访问,就不再从它出发进行搜索。
遍历图的实质上是对每个顶点查找其邻接点的过程。其耗费的时间则取决于所采用的存储结构。
用邻接矩阵存储图时,查找每个顶点的邻接点需要O(n2);//找每个点的邻接点都要到对应的行去遍历一遍
用邻接表存储图时,查找每个顶点的邻接点需要O(e);//只访问了每条边
n—图中顶点的个数;
e—边数/弧数
当以邻接表作存储结构时,深度优先遍历的时间复杂度为O(n+e)//初始化+遍历
矩阵的话是O(n+n2)=O(n2)
另外在后面的求拓扑排序的序列时也可以借助深度优先遍历得到
2. 广度优先遍历
思想:
①从图中的某个顶点v0出发,访问此顶点,
②依次访问v0的所有未被访问过的邻接点,之后按这些顶点被访问的先后次序依次访问它们的邻接点,直至图中所有和v0有路径相通的顶点都被访问到。
③若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
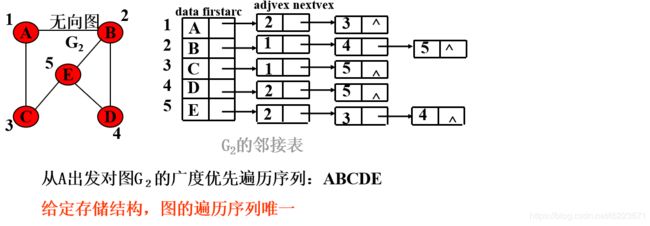
时间复杂度深度优先遍历。
代码
有向和无向图的区别就是,在建立邻接矩阵或者邻接表时,前者一次建立两条对称关联,后者只建立一条,稍作改动即可相互转换。而网和图的区别,前者把权值全赋值为0,后者用户自己输入,这里以无向图为例
里面用到了用户自定义头文件,如果不知道怎么建立,请参照如何建立和调用用户自定义的头文件
#include<stdio.h>
#include<stdlib.h>
#include<limits.h>//包含c语言里的最大值INT_MAX最小值INT_MIN
#define INFINITY INT_MAX//INT_MAX=2^31-1
#define MAX_VERTEX_NUM 20
#define MAX 100
#define ERROR 0
#define OVERFLOW 0
#define TRUE 1
#define FALSE 0
#define OK 1
typedef int VRType ;
typedef int InfoType ;
typedef char VertexType ;//顶点的标识类型
typedef int Status;
typedef enum {DG,DN,UDG,UDN} GraphKind;//省略枚举类型变量名
typedef struct ArcCell{
VRType adj; //VRType是定点关系类型,对无权图,用0或1;对带权图表示权值类型
InfoType *info;//表示该弧相关信息的指针
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
//临接矩阵的二维数组定义
#include"queuevex.h"
typedef struct{
VertexType vexs[MAX_VERTEX_NUM]; //顶点向量
AdjMatrix arcs; //邻接矩阵
int vexnum,arcnum; //图的当前顶点数和弧度
int kind; //图的种类标志
}MGraph; //kind这种的图的所有信息的定义
Status CreatUDN(MGraph &G);
Status CreatGraph(MGraph &G)
{
printf("please input the kind of graph\n");
scanf("%d", &G.kind);
switch(G.kind)
{
// case DG:return CreatDG(G);//构造有向图
// case DN:return CreatDN(G);//构造无向图
// case UDG:return CreatUDG(G);//构造无向网
case UDN:return CreatUDN(G);//构造无向网
default: return ERROR;
}
}
int LocateVex(MGraph &G,char v)
{ for(int i=0;i<G.vexnum;i++)
if(G.vexs[i]==v)
return i;
}
Status CreatUDN(MGraph &G) //在邻接矩阵存储结构上,构造无向网G
{
char v1,v2;
int w;
printf("请输入无向网的顶点数和边数");
scanf("%d%d",&G.vexnum,&G.arcnum);//读入顶点和边数目
printf("请按顺序输入节点标识符");
for(int i=0;i<G.vexnum;i++)
scanf(" %c",&G.vexs[i]); //构造顶点向量,用来表示行坐标或者列坐标,因为临接矩阵是没有位置来存表头的
printf("%c%c",G.vexs[0],G.vexs[1]);
for(int i=0;i<G.vexnum;i++) //邻接矩阵初始化
for(int j=0;j<G.vexnum;j++)
{
G.arcs[i][j]={INFINITY,NULL};
for(int k=0;k<G.arcnum;k++)//构造邻接矩阵
{
printf("请依次输入每条边依附的顶点和权值");
scanf(" %c %c %d",&v1,&v2,&w); //读入一条边依附的顶点及权值
int i=LocateVex(G,v1);
int j=LocateVex(G,v2);//确定v1、v2在图中的位置
G.arcs[i][j].adj=w;//边的权值
G.arcs[j][i]=G.arcs[i][j];//置的对称弧
} return OK;
}
}//CreateUDN
void PrintMap(MGraph G)
{
int i=0,j=0;
for(i=0;i<G.vexnum;i++)
{
printf("%5c",G.vexs[i]);
for(j=0;j<G.vexnum;j++)
{if(G.arcs[i][j].adj==INFINITY)
printf("%5s","oo");
else printf("%5d",G.arcs[i][j].adj);
}
printf("\n");
}
}
int visited[MAX];
//邻接矩阵的深度优先遍历
void DFS(MGraph G, int i)
{
int j;
visited[i] = TRUE;
printf("%c ", G.vexs[i]);
for (j=0; j<G.vexnum; ++j)
{
if (G.arcs[i][j].adj!=INFINITY && !visited[j])
DFS(G, j);
}
}
void DFSTraverse(MGraph G)
{
int i;
for (i=0; i<G.vexnum; i++)
visited[i] = FALSE;
for (i=0; i<G.vexnum; i++)
{
if (!visited[i])
DFS(G, i);
}
}
//邻接矩阵的广度优先遍历
void BFSTraverse(MGraph &G)
{
int i, j;
SqQueue Q;
for (i=0; i<G.vexnum; ++i)
visited[i] = FALSE;
InitQueue(Q);
for (i=0; i<G.vexnum; ++i)
{
if (!visited[i])
{
printf("%c", G.vexs[i]);
visited[i] = TRUE;
EnQueue(Q, i);
while (!QueueEmpty(Q))
{
DeQueue(Q, i);
for (j=0; j<G.vexnum; ++j)
{
if (!visited[j] && G.arcs[i][j].adj!=INFINITY)
{
visited[j] = TRUE;
printf("%c", G.vexs[j]);
EnQueue(Q, j);
}
}
}
}
}
}
typedef struct ArcNode//定义表节点
{
int adjvex;//该弧所指的顶点位置
struct ArcNode *nextarc;//指向下一条弧的指针
InfoType *info;//该弧相关信息的指针
}ArcNode;
typedef struct Vnode//定义头结点
{
VertexType data;//顶点的信息
ArcNode *firstarc;//指向第一条依附于该顶点的弧的指针
}VNode,AdjList[MAX_VERTEX_NUM];//头结点是个一维j结构体数组
typedef struct//定义邻接表
{
AdjList vertices;//头结点的一维数组
int vexnum,arcnum;//图的当前顶点数和弧数
int kind;//图的种类
}ALGraph;
void CreatAlgraph(ALGraph &G)//创建以邻接表为存储结构的无向图
{
int n,e;
printf("请输入顶点和边的数目");
scanf("%d%d",&G.vexnum,&G.arcnum);//读入顶点的数目
n=G.vexnum; e=G.arcnum;
printf("请依次输入顶点的值");
for(int i=1;i<=n;i++) //读入顶点值
{
scanf(" %c",&G.vertices[i].data);
G.vertices[i].firstarc=NULL;
}
printf("请依次输入有关联的结点序号");
for(int i=1;i<=e;i++)//建立边()的信息
{
int s,d;
ArcNode*p,*q;
scanf("%d%d",&s,&d);//读入顶点序号
p=(ArcNode*)malloc(sizeof(ArcNode));//建立表节点
q=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=d;//给弧所指的节点赋值
q->adjvex=s;
p->nextarc=G.vertices[s].firstarc;G.vertices [s].firstarc=p;//这是一种逆向建立链表的方法
q->nextarc=G.vertices[d].firstarc;G.vertices[d].firstarc=q;//效果展示
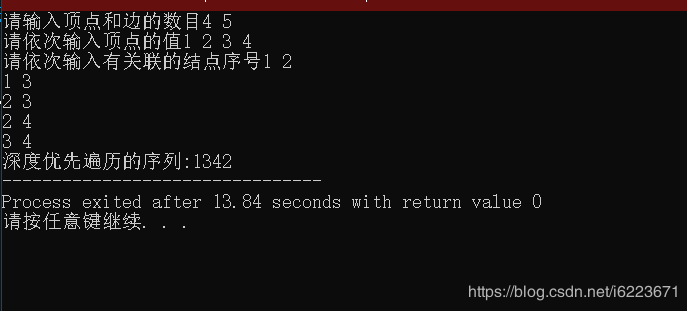
头文件代码
#include"queuevex.h"
#define STACK_INIT_SIZE 100
#define MAXQSIZE 100
typedef int QElemType;
typedef struct
{
QElemType *base;
int front;
int rear;
}SqQueue;
Status QueueEmpty(SqQueue Q)//栈空返回1,不空返回0
{
if(Q.rear==Q.front)
return OK;
else return ERROR;
}
Status InitQueue(SqQueue &Q)
{
Q.base=(QElemType*)malloc(MAXQSIZE*sizeof(QElemType));
if(!Q.base) return OVERFLOW;
Q.front=Q.rear=0;
return OK;
}
int QueneLength(SqQueue Q)
{
return(Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;
}
Status EnQueue (SqQueue &Q,QElemType e)
{
if((Q.rear+1)%MAXQSIZE==Q.front) return ERROR;
Q.base[Q.rear]=e;
Q.rear=(Q.rear+1)%MAXQSIZE;
return OK;
}
Status DeQueue(SqQueue &Q,QElemType &e)
{
if(Q.front==Q.rear) return ERROR;
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXQSIZE;
return OK;
}