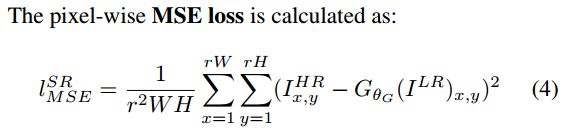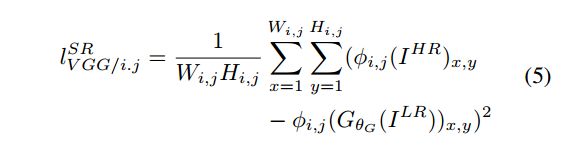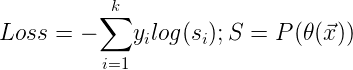【机器学习】——专题学习：(1)损失函数loss积累
目录
一、超分辨率重建loss
1、感知损失（Perceptual Losses）
二、生成对抗
1、GAN原始损失。
三、语义分割
1、语义分割损失。
未分类
1、对比损失 (Contrastive Loss)
2、余弦损失(discrepancy loss)。link
3、交叉熵损失。
一、超分辨率重建loss
1、感知损失（Perceptual Losses）
论文地址
动机：MSE损失能够取得很高的PSNR，但是对图片高频部分(边缘)会过去平滑，如图：
方法：与比较pixel-wised的loss不同，将原始图片与生成图片都通过一个CNN，变成比较feature_map-wised的loss。
二、生成对抗
1、GAN原始损失。
论文地址
以下GAN的原始损失解释大部分转载自https://www.cnblogs.com/walter-xh/p/10051634.html
GAN的原始损失函数是这样的
损失函数定义：
注意：公式中的E是指一个batch数据的平均_link。
一切损失计算都是在D（判别器）输出处产生的，而D的输出一般是fake/true的判断，所以整体上采用的是二进制交叉熵函数。
左边包含两部分minG和maxD。
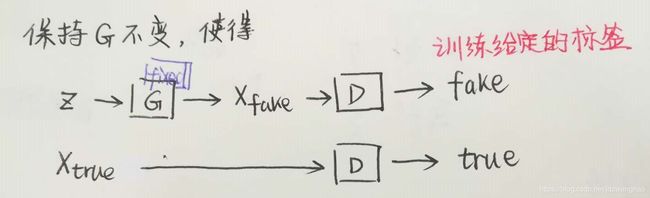
首先看一下maxD部分。maxD就是保持G不变，训练D来尽可能max 
。因为训练一般是先保持G（生成器）不变训练D的。D的训练目标是正确区分fake/true，如果我们以1/0代表true/fake，则对第一项E因为输入采样自真实数据所以我们期望D(x)趋近于1，也就是第一项更大。同理第二项E输入采样自G生成数据，所以我们期望D(G(z))趋近于0更好，也就是说第二项又是更大。所以是这一部分是期望训练使得整体更大了，也就是maxD的含义了。
maxD部分训练样本以及对应标签的给定
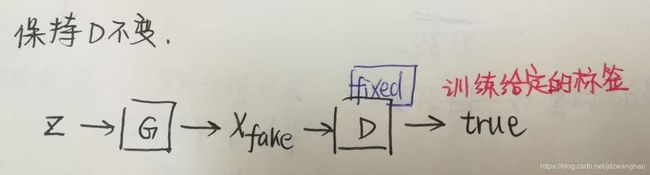
第二部分minG部分。minG就是保持D不变，训练G来尽可能min 。这个时候只有第二项E有用了，关键来了，因为我们要迷惑D，所以这时将label设置为1(我们知道是fake，所以才叫迷惑)，希望D(G(z))输出接近于1更好，也就是这一项越小越好，这就是minG。当然判别器哪有这么好糊弄，所以这个时候判别器就会产生比较大的误差，误差会更新G，那么G就会变得更好了，这次没有骗过你，只能下次更努力了。
minG部分训练样本以及对应标签的给定
三、语义分割
1、语义分割损失。
标准语义分割损失
普通分类问题与语义分割分类问题的区别。体现在loss就是普通分类中 
和 
都为1。
普通分类
语义分割
未分类
1、对比损失 (Contrastive Loss)
论文地址
以下转载自Link
在孪生神经网络（siamese network）中，其采用的损失函数是contrastive loss，这种损失函数可以有效的处理孪生神经网络中的paired data的关系。contrastive loss的表达式如下：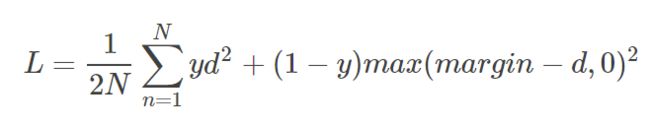 
其中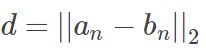
，代表两个样本特征的欧氏距离，y为两个样本是否匹配的标签，y=1代表两个样本相似或者匹配，y=0则代表不匹配，margin为设定的阈值。
观察上述的contrastive loss的表达式可以发现，这种损失函数可以很好的表达成对样本的匹配程度，也能够很好用于训练提取特征的模型。当y=1（即样本相似）时，损失函数只剩下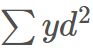
，即原本相似的样本，如果在特征空间的欧式距离较大，则说明当前的模型不好，因此加大损失。而当y=0时（即样本不相似）时，损失函数为
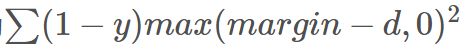，即当样本不相似时，其特征空间的欧式距离反而小的话，损失值会变大，这也正好符号我们的要求。
这张图表示的就是损失函数值与样本特征的欧式距离之间的关系，其中红色虚线表示的是相似样本的损失值，蓝色实线表示的不相似样本的损失值。
2、余弦损失(discrepancy loss)。link
余弦损失最大的作用就是能够增大两个分布之间的差异性。为什么说是增大呢，因为 
的时候，实际上就是 
，其中，
就是 
与 
之间的夹角。当 
时，
最小，而此时， 与 在角度上差异最大。
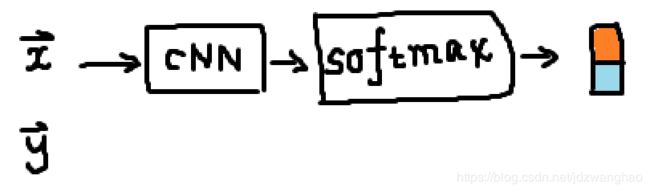
3、交叉熵损失。
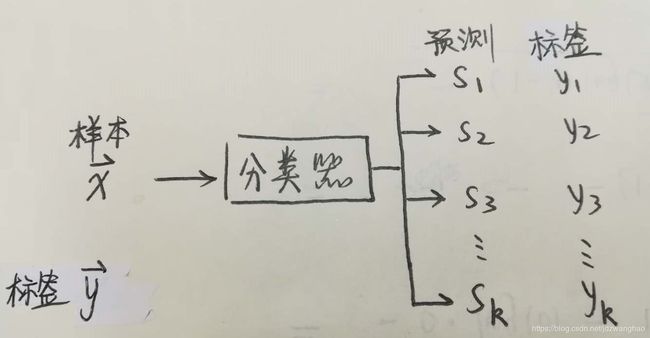
【单个样本的分类情况】
# --- 多分类时 ---#
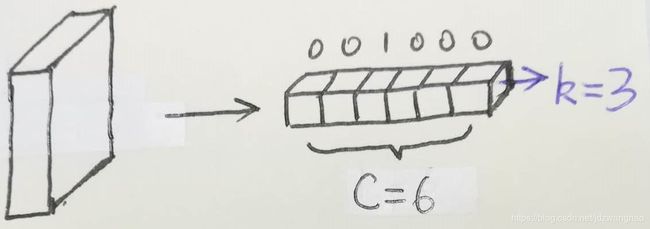
单个样本输入为 
，其中 
为one-hot编码的标签[0, 0, 0, 1, 0]，公式如下：
输入输出
其中，
： 表示分类的类别总数。
： 表示分类器中分类口的位置。
： 表示当前输入 
的第 个分类口的预测概率输出。（注：one-hot编码使得每个分类口都有值）
： 表示当前输入 的第 个分类口的标签值。（注：one-hot编码使得每个分类口都有值）
： 表示概率分布预测函数，one-hot编码的多分类的一般采用 softmax函数，输出是各个类别的概率。
# --- 二分类时 ---#
情况1： 是softmax函数，输出是二维，标签 采用二维one-hot编码。使用上面多分类。
标题
![\large Loss= - [ \hat{y_{1}}log(s_{1}) +\hat{y_{2}}log(s_{2})]; s_{1}=P(\theta(\vec{x})),s_{2}=P(\theta(\vec{x}))](http://img.e-com-net.com/image/info8/cd711b9999f14ed6ace845e19f2ddcee.gif){kind=small}
公式中有两个logit ( 
)，那么就是cross-entropy的损失。
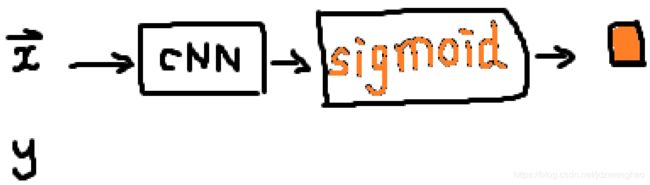
情况2： 是sigmoid函数，输出是一维，标签 
是标量
标题
单个样本 
，公式如下：丨公式推导丨
![\large Loss = - [ ylog(s) + (1-y)log(1-s)]; S=P(\theta(\vec{x}))](http://img.e-com-net.com/image/info8/81a10fad56de41579ea716e439631e91.gif){kind=small}
其中，
： 表示当前输入 
的标签值，是一维标量。
： 表示sigmoid函数的预测概率，是一维标量，
。
【多个样本（batch）的分类情况】
# --- 多分类时 ---#
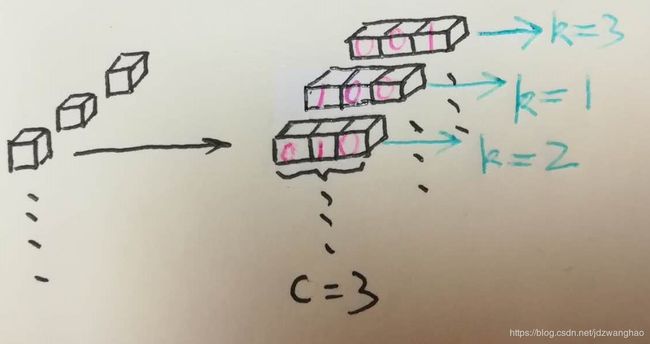
多个样本输入为 ，其中 为one-hot编码的标签[0, 0, 0, 1, 0]，公式如下：
### 资料
丨资料1丨
4、中心损失（Center Loss）
原始论文链接：link