[人脸关键点检测] Wing loss 论文解读
转载请注明作者和出处: http://blog.csdn.net/john_bh/
论文链接:Wing Loss for Robust Facial Landmark Localisation with Convolutional Neural Networks
作者及团队:萨里大学 & 江南大学
会议及时间:CVPR 2018
code:原作者开源github 地址
code:github 地址
文章目录
- 论文解读
- 1.主要贡献
- 2.分析比较 L 1 , L 2 和 s m o o t h L 1 L1,L2和smooth_{L1} L1,L2和smoothL1损失函数
- 3. w i n g l o s s wing\ loss wing loss
- 4.Pose-based data balancing
- 5.Two-stage landmark localisation
- 6.实验结果
论文解读
wing loss被CVPR2018收录, 是由萨里大学研究人员(第一至四作者)与江南大学研究人员(第五作者)共同研究。
1.主要贡献
- 基于CNN的基于回归的面部界标定位的不同损失函数的系统分析,从经验和理论上比较L1,L2和平滑L1损失函数,发现L1和平滑L1的性能要比广泛使用的L2损失好得多。对于基于CNN的定位模型的训练,应更加关注中小范围误差;
- 提出了一个新的损失函数Wing loss,旨在提高深度网络训练过程中应对小范围和中等范围内的误差的能力;
- 提出了基于人脸姿态的的数据平衡策略,可以补偿训练集中头部姿势旋转较大的样本少的问题,主要解决训练数据平衡性问题;
- 提出一个二阶段的人脸关键点检测网络框架;
2.分析比较 L 1 , L 2 和 s m o o t h L 1 L1,L2和smooth_{L1} L1,L2和smoothL1损失函数
给定一个图像 I I I和一个网络 Φ \Phi Φ,可以预测人脸关键点的vetor: s ‘ = Φ ( I ) s^`=\Phi(I) s‘=Φ(I).损失函数是:
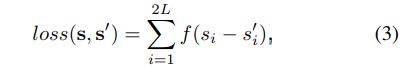
其中 s s s是人脸关键点的ground-truth,函数 f ( x ) f(x) f(x)就等价于:
- L 1 l o s s L1 \ loss L1 loss
L 1 ( x ) = ∣ x ∣ L1(x)=|x| L1(x)=∣x∣ - L 2 l o s s L2 \ loss L2 loss
L 2 ( x ) = 1 2 x 2 L2(x)=\frac{1}{2}x^2 L2(x)=21x2 - S m o o t h L 1 ( x ) Smooth_{L1}(x) SmoothL1(x):
s m o o t h L 1 ( x ) = { 1 2 x 2 i f ∣ x ∣ < 1 ∣ x ∣ − 1 2 o t h e r w i s e smooth_{L1}(x)=\begin{cases} \frac{1}{2}x^2&if|x|<1 \\ |x|-\frac{1}{2} & otherwise\end{cases} smoothL1(x)={21x2∣x∣−21if∣x∣<1otherwise
损失函数对 x x x的导数分别为:
d L 2 ( x ) d x = x \frac{dL_2(x)}{dx}=x dxdL2(x)=x
d L 1 ( x ) d x = { 1 i f x ≥ 0 − 1 o t h e r w i s e \frac{dL_1(x)}{dx}= \begin{cases} 1 & if \ x\ge0 \\ -1 & otherwise \end{cases} dxdL1(x)={1−1if x≥0otherwise
d s m o o t h L 1 ( x ) d x = { x i f ∣ x ∣ < 1 ± 1 o t h e r w i s e \frac{d\ smooth_{L1}(x)}{dx}= \begin{cases} x & if \ |x|\ <1 \\ \pm1 & otherwise \end{cases} dxd smoothL1(x)={x±1if ∣x∣ <1otherwise
L 2 L2 L2损失函数,当 x x x增大时 L 2 l o s s L2\ loss L2 loss对 x x x的导数也增大,这就导致训练初期,预测值与ground-truth差异过大时,损失函数对预测值的梯度十分大,导致训练不稳定。
L 1 l o s s L1\ loss L1 loss的导数为常数,在训练后期,预测值与ground-truth差异很小时, 损失对预测值的导数的绝对值仍然为1,此时学习率(learning rate)如果不变,损失函数将在稳定值附近波动,难以继续收敛达到更高精度。
s m o o t h L 1 smooth_{L1} smoothL1损失函数, 在 x x x 较小时,对 x x x的梯度也会变小,而在 x x x很大时,对 x x x的梯度的绝对值达到上限 1,也不会太大以至于破坏网络参数。 s m o o t h L 1 smooth_{L1} smoothL1完美地避开了 L 1 L_1 L1和 L 2 L_2 L2损失的缺陷。此外,根据fast rcnn的说法,"… L1 loss that is less sensitive to outliers than the L2 loss used in R-CNN and SPPnet." 也就是 s m o o t h L 1 smooth_{L1} smoothL1让loss对于离群点更加鲁棒,即相比于 L 2 L_2 L2损失函数,其对离群点、异常值(outlier)不敏感,梯度变化相对更小,训练时不容易跑飞。
图3描绘了这些损失函数的曲线图。需要注意的是, S m o o l t h L 1 Smoolth_{L1} SmoolthL1损失是Huber损失的一种特殊情况,L2损失函数在人脸关键点检测中被广泛应用,然而,L2损失对异常值很敏感。![[人脸关键点检测] Wing loss 论文解读_第2张图片](http://img.e-com-net.com/image/info8/9c4c06a5e8ef437bb5675d0bbd544e23.jpg)
作者选了三个模型作为比较的baseline:
- CCL:基于随机深林的多视角级联回归方法,CVPR 2016
- TR-DRN:两阶段的重新初始化的深度回归网络,CVPR 2017
- DAC-CSR:基于级联形状的回归方法,CVPR 2017
使用三种不同的损失函数对CNN-6网络进行AFLW-full训练,结果如表1所示。
![[人脸关键点检测] Wing loss 论文解读_第3张图片](http://img.e-com-net.com/image/info8/3fcf362980934a30bd58e006872559a9.jpg)
L 2 L2 L2损失函数结果在准确性方面比CCL好,但比DAC-CSR和TR-DRN差。 令人惊讶的是, L 1 L1 L1或 S m o o l t h L 1 Smoolth_{L1} SmoolthL1进行CNN-6训练时,尽管CNN网络很简单,但在准确性方面的性能却显着提高,并且优于所有最新的baseline方法。
3. w i n g l o s s wing\ loss wing loss
在图4中通过绘制累积误差分布(CED,Cumulative Error Distribution)曲线,比较使用的简单CNN-6网络在AFLW数据集上获得的结果。可以看到,上一部分中分析的所有损失函数在出现较大误差时表现良好。 这说明神经网络的训练应更多地关注具有小或中误差的样本。 为了实现此目标,提出了一种新的损失函数,即基于CNN的面部标志定位的机翼损失。
![[人脸关键点检测] Wing loss 论文解读_第4张图片](http://img.e-com-net.com/image/info8/22d0c2fce197492d94e26f9dfbfef891.jpg)
说明:
当NME在0.04的时候,测试数据比例已经接近1了,所以在0.04到0.05这一段,也就是所谓的large errros段,并没有分布更多的数据,说明各损失函数在large errors段都表现很好。模型表现不一致的地方就在于small errors和medium errors段,例如,你在NME为0.02的地方画一根竖线,一目了然。基于此,作者提出训练过程中应该更多关注samll or medium range errros样本。
直接分析公式3( L 1 和 L 2 L_1 和L_2 L1和L2),这两个函数的梯度大小分别为1和 ∣ x ∣ |x| ∣x∣,对应的优化步长大小为 ∣ x ∣ |x| ∣x∣和1.但是,当我们尝试同时优化多个点的位置时,情况变得更加复杂。 在 L 1 L_1 L1的情况下,所有点的梯度大小都相同,但是优化步长受较大误差的影响(随误差增大而增加)。 对于 L 2 L_2 L2,优化步长是相同的,但梯度将由较大的误差决定。在这两种情况下,两个loss都受到大的误差的影响,对大误差敏感。 因此,在两种情况下都很难校正较小的偏移。
优化步长:优化步长指得是要达到最优化,需要迭代的次数(步数);L1的梯度是固定的,所以误差越大,采用L1优化就需要更多的迭代次数,也就是他说的“优化步长随着误差增大而增大”;反之,L2的梯度跟误差是成正比的。例如:你与目标距离有100公里,假设没次前进0.01(学习率);第一次L2梯度是100,你前进1000.01=1公里,第二次,还有99公里,梯度就是99,则一步前进990.01=0.99公里,以此类推;而L1的梯度固定是1,则每次前进1*0.01=0.01公里
可以使用 l n x ln\ x ln x来增强小误差的影响,它的梯度是 1 x \frac {1}{x} x1,对于接近0 的值就会越大,optimal step size为 x 2 x^2 x2,这样gradient就由small errors“主导”,step size由large errors“主导”。这样可以恢复不同大小误差之间的平衡。 但是,为了防止在可能的错误方向上进行较大的更新步骤,重要的是不要过度补偿较小的定位错误的影响。 这可以通过选择具有正偏移量的对数函数来实现。
但是这种类型的损失函数适用于处理相对较小的定位误差。 在wild 人脸关键点检测中,我们可能会处理极端姿势,这些姿势最初的定位误差可能非常大,在这种情况下,损失函数应促进从这些大错误中快速恢复。 这表明损失函数的行为应更像 L 1 L_1 L1或 L 2 L_2 L2。 由于 L 2 L_2 L2对异常值敏感,因此选择了 L 1 L_1 L1。
所以,对于小误差,它应该表现为具有偏移量的对数函数,而对于大误差,则应表现为L1。这样的复合损失函数可以定义为:

- w w w:正数 w w w将非线性部分的范围限制在 [ − w , w ] [-w,w] [−w,w]区间内;
- ϵ \epsilon ϵ:约束非线性区域的曲率,并且 C = w − w l n ( 1 + x ϵ ) C=w-wln(1+\frac{x}{\epsilon}) C=w−wln(1+ϵx)是一个常数,可与平滑的来连接分段的线性和非线性部分。 ϵ \epsilon ϵ的取值是一个很小的数值,因为它会使网络训练变得不稳定,并且会因为很小的误差导致梯度爆炸问题。
实际上,的Wing loss函数的非线性部分只是简单地采用 l n ( x ) ln(x) ln(x)在 [ ϵ / w , 1 + ϵ / w ] [\epsilon/ w,1 +\epsilon/ w] [ϵ/w,1+ϵ/w]之间的曲线,并沿 X X X轴和 Y Y Y轴将其缩放比例为 w w w。 另外,我们沿 Y Y Y轴应用平移以使wing(0)= 0,并在损失函数上施加连续性。
在实验中,将wing loss的参数设置为 w = 10 w = 10 w=10和 ϵ = 2 \epsilon=2 ϵ=2。有关不同参数设置的结果,请参阅表2。
![[人脸关键点检测] Wing loss 论文解读_第5张图片](http://img.e-com-net.com/image/info8/1ce5b23acca1439ebf96cbc8061b8bfd.jpg)
4.Pose-based data balancing
为了解决人脸姿势不平衡造成的模型性能不佳的问题,作者提出了基于人脸姿势的数据平衡策略PDB(Pose-based Data Balancing)。例如:在给定训练数据集的情况下,其中的大多数样本很可能是正脸数据。在这样的数据集上训练的神经网络主要是正面的。通过过度拟合正面姿势,它无法很好地适应具有较大姿势的脸部。
PDB方法:首先使用Procrustes Analysis将所有训练形状与参考形状对齐,并以平均形状作为参考形状。将对齐后的training shapes进行PCA,用shape eigenvector将original shapes进行投影至一维空间,用来控制姿态变化。训练样本的投影系数分布由带有K个bin的直方图表示,如图5所示:
![[人脸关键点检测] Wing loss 论文解读_第6张图片](http://img.e-com-net.com/image/info8/0a6a6b9963e840e28f5bfd000df8f439.jpg)
作者通过复制落入较低占用率的bin中的样本来平衡训练数据,主要方法有随机旋转,边界框扰动和其他数据增强方法来修改每个重复的样本,增加角度大人脸的数据。
5.Two-stage landmark localisation
除了out-of-plane head rotations外,人脸关键点检测的准确性还有其他因素,例如:in-plane head rotations,不准确的bounding box。为了解决这个问题,作者提出了两阶段人脸关键点检测的框架。如下图所示:
![[人脸关键点检测] Wing loss 论文解读_第7张图片](http://img.e-com-net.com/image/info8/f3e638e5ee6a491cb1b59de3782cc0c4.jpg)
在提出的两阶段定位框架中, 64 × 64 × 3 64×64×3 64×64×3输入图像的CNN-6网络作为第一个网络。 CNN-6网络输出的人脸关键点可通过消除in-plane head rotation并校正边界框,给第二网络的提供更好的输入信息。
“ CNN-7”用于表示第二个网络, CNN-7与CNN-6具有类似的体系结构。不同之处:
- CNN-7具有6个卷积层,通过添加一组卷积,Relu和Max池化层,可将特征图的大小从 128 × 128 × 3 128×128×3 128×128×3调整为 2 × 2 × 512 2×2×512 2×2×512。
- CNN-7中的第一个卷积层,将3×3内核的数量从32倍增加到64。
- CNN-7输入图像分辨率是 128 × 128 × 3 128×128×3 128×128×3,CNN-6输入图像分辨率 64 × 64 × 3 64×64×3 64×64×3。
因此,将“ CNN-6 / 7”一词用于两阶段面部界标定位框架,并将其它模型比较如表3所示:应注意的是PDB可以改善CNF-6在AFLW数据集上针对所有不同类型的损失函数的性能。
6.实验结果
- AFLW 实验结果
如图6所示,即使使用常用的 L 2 L_2 L2损失函数(洋红色实线)进行训练,CNN-6 / 7网络也胜过所有其他方法。 这验证了所提出的两阶段本地化框架和PDB策略的有效性。 其次,只需将损失函数从 L 2 L_2 L2切换到 L 1 L_1 L1或 s m o o t h L 1 smooth_{L1} smoothL1,两阶段方法的性能就得到了显着改善(红色实线和黑色虚线)。 最后,使用 w i n g l o s s wing\ loss wing loss函数可进一步提高准确性(黑色实线)。 与小到中等归一化平均误差(X轴)相关的测试样本(Y轴)的比例增加。
![[人脸关键点检测] Wing loss 论文解读_第9张图片](http://img.e-com-net.com/image/info8/543bdbaeef284c5d9ebad68ad55c0532.jpg)
- 300-W数据集上实验结果:
如表4所示,采用PDB策略和新提出的Wing损失函数的两阶段地标定位框架在准确性上优于300W数据集上的所有其他最新算法。 与RAR算法报告的当前最佳结果相比,该错误已减少了近20%。
![[人脸关键点检测] Wing loss 论文解读_第10张图片](http://img.e-com-net.com/image/info8/eccfed581f1f4a10b9d43f287012a361.jpg)
- 不同网络结构上的对比实验:
![[人脸关键点检测] Wing loss 论文解读_第11张图片](http://img.e-com-net.com/image/info8/2ddbacebeea24440a2cd3946f8141e5c.jpg)
- 模型参数量,大小和推理速度对比结果:
![[人脸关键点检测] Wing loss 论文解读_第12张图片](http://img.e-com-net.com/image/info8/fc332a5c63694907883f285db5e86345.jpg)
![[人脸关键点检测] Wing loss 论文解读_第1张图片](http://img.e-com-net.com/image/info8/d95bbd0f143e49d788534ce036622e3c.jpg)
![[人脸关键点检测] Wing loss 论文解读_第8张图片](http://img.e-com-net.com/image/info8/b1b25a06e0e241b3a04d0eb6fda6ae54.jpg)