Huffman编码与解码 （Huffman编码、二叉树）

Huffman编码与解码

[问题描述]

对一篇不少于2000字符的英文文章（source.txt），统计各字符出现的次数，实现Huffman编码(code.dat)，以及对编码结果的解码(recode.txt)。

[基本要求]

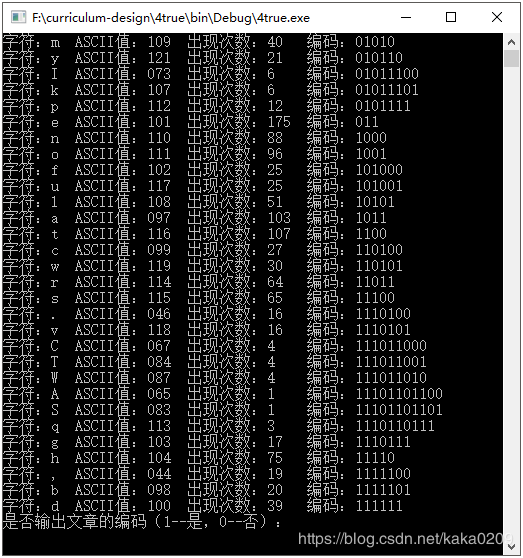
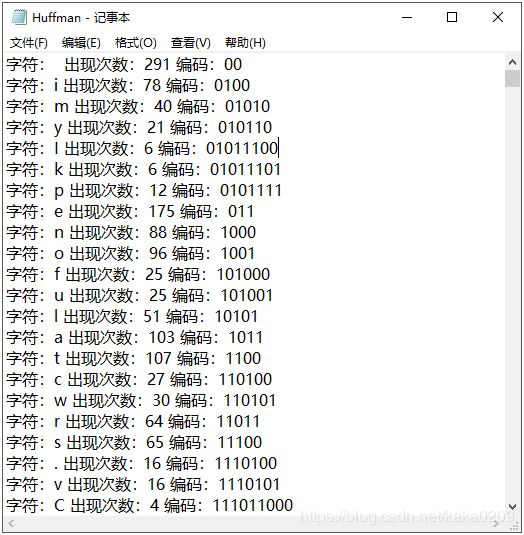
（1） 输出每个字符出现的次数和编码,并存储文件(Huffman.txt)。

（2） 在Huffman编码后，英文文章编码结果保存到文件中(code.dat)，编码结果必须是二进制形式，即0 1的信息用比特位表示，不能用字符’0’和’1’表示。

（3） 实现解码功能。

数据结构

//二叉树
typedef struct
BiTNode
{
    int data;//权值
    int word=300;//字母
    int HuffmanCode[100];
    struct BiTNode *lchild , *rchild;
}BiTNode ,
*BiTree;

算法设计思想

1.建立一个zm数组，从文件中一个个读取文章数据，利用哈希表的思想，根据所得字符的ASCII值在数组里分配地址，并对其值加一，以此统计字符的出现次数。

2.建立一个值为树结点的数组，存储文章的字符，每次选出ASCII值最小的两个字符作为新结点的左右子树，将新节点的权值置为左、右子树上根结点的权，即为ASCII值的和，再将刚刚所选的字符从数组里删除。重复上述步骤，直到构建出一个二叉树为止。

3.设置数组存储编码，利用中序遍历依次递归遍历哈夫曼树，对哈夫曼树中存储的字符调用编码函数进行编码，编码函数也用递归实现，向左走为0，向右为1。

4.对树中结点编码完毕后，从文章中依次读取字符，在树中查找相应的字符并存储编码到文件中；

5.最后再从文件中读取哈弗曼编码，在树中查找字符，0便进入左子树，1便进入右子树，找到后直接输出。

算法时间复杂度

BiTree CreateHuffman( int a[],BiTree &T ) //创建哈夫曼树

时间复杂度：O(n*logn)

void Creat_HCode (BiTree T , BiTree B ) //利用递归依次创建编码

时间复杂度：O(n*logn)

void bianma_T1 (BiTree T, int b[], int ch, int n ) //创建字符ch的编码

时间复杂度：O(n*logn)

本来想把代码贴全的，但是粘过来一直乱码，我也不知道为啥，之后有时间的话可能会直接上传资源吧，主要部分代码先贴出来。
部分代码如下：

//创建字符ch的编码
void bianma_T1 ( BiTree T, int b[], int ch, int n )
{
    int i;
    if ( T )
    {
        if ( ch == T->word )//复制编码
        {
            b[0] = n;//存储编码长度
            for( i=0; i<=n; i++ )
            {
                T->HuffmanCode[i] = b[i];
            }
        }
        else
        {
            b[n]=0;
            bianma_T1 ( T->lchild , b ,  ch , n+1 );
            b[n]=1;
            bianma_T1 ( T->rchild , b , ch , n+1  );
        }
    }
}



//根据输入的字符输出编码
void bianma_T ( BiTree T , int b[], int ch , int n  )
{
    int i;
    if( T )
    {
        if( ch == T->data )
        {
             b[0] = n;
             for ( i=1; i<=n; i++ )
                cout<< b[i];
             cout<< endl;
        }
        else
        {
            b[n]=0;
            bianma_T1 ( T->lchild , b ,  ch , n+1 );
            b[n]=1;
            bianma_T1 ( T->rchild , b , ch , n+1  );
        }
    }
}
//利用递归依次创建编码
void Creat_HCode ( BiTree T ,  BiTree B )
{
    if ( T == NULL )
    {
        cout<<"此数为空"<<endl;
        return;
    }
    else
    {
      if ( T->word!=300 )//若此节点为文章内的字符，则对它进行编码
      {
          int ch = T->word;
          int b[100];
          bianma_T1 ( B , b , ch , 1);
      }
      Creat_HCode ( T->lchild , B );
      Creat_HCode ( T->rchild , B);
    }
}


//返回哈夫曼树的深度
int BTreeDepth ( BiTree &T )
{
    int ldepth , rdepth;
    if ( T == NULL )
    {
         cout<<"此数为空"<<endl;
         return 0;
    }
    else
    {
        ldepth = BTreeDepth ( T -> lchild );
        rdepth = BTreeDepth ( T -> rchild );
    }
    if ( ldepth > rdepth )
        return ( ldepth + 1 );
    else return ( rdepth + 1 );
}
//创建哈夫曼树
BiTree CreateHuffman( int a[],BiTree &T )
{
    int i=0, j,k;
    BiTree b , q;
    BiTree keep[max];
    for ( k=0, j=0; j<max; j++ ) //初始化keep指针数组，使每个指针元素指向a数组中对应的元素结点
    {
        if ( a[j]!=0 )
        {
            b = (BiTNode *) malloc ( sizeof(BiTNode) );
            b->data = a[j];
            b->word = j;
            b->lchild = b->rchild = NULL;
            keep[k] = b;
            k++;
        }
    }
    //建立哈夫曼树
    for ( i=1; i<k; i++ )
    {
        int small = -1, big;
        //让small初始指向森林中第一棵树，big指向第二棵
        for ( j=0; j<k; j++ )
        {
            if ( keep[j]!= NULL && small==-1 )
            {
                small = j;
                continue;
            }
            if ( keep[j]!= NULL )
            {
                big = j;
                break;
            }
        }
        //从当前森林中求出最小权值树和次最小
        for ( j=big; j<k; j++)
        {
            if ( keep[j]!= NULL)
            {
                if ( keep[j]->data < keep[small]->data )
                {
                    big = small ;
                    small  = j;
                }
                else if ( keep[j]->data < keep[big]->data )
                    big = j;
            }
        }
        //由最小权值树和次最小权值树建立一棵新树，q指向树根结点
        q = (BiTNode *) malloc ( sizeof(BiTNode) );
        q->data = keep[small]->data + keep[big]->data;
        q->word = 300;
        q->lchild = keep[small];
        q->rchild = keep[big];
        keep[small] = q;//将指向新树的指针赋给b指针数组中small位置
        keep[big] = NULL;
    }
    if( b != NULL)
    {
        free(b);
        b = NULL;
    }
    T = q;
}


//根据编码查找匹配的字符
int jiema ( BiTree T, int H[] )
{
    int i=0;
    for( i=1; i<H[0]; i++ )
    {
        if( H[i]==0 )
        T = T->lchild;
        else if ( H[i]==1 )
        T = T->rchild;
    }
    return T->word;
}

测试用例：

结果：输出哈夫曼树，并存储到文件里

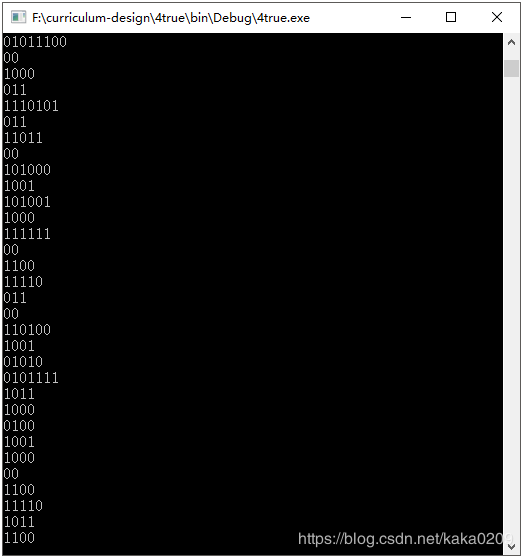
输出文章的解码：（取一小部分展示）